湖南省常德市2019年中考数学4月模拟试卷
试卷更新日期:2020-05-09 类型:中考模拟
一、选择题
-
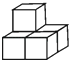
1. ⊙O的半径为5cm,点A到圆心O的距离OA=3cm,则点A与⊙O的位置关系为( )A、点A在⊙O上 B、点A在⊙O内 C、点A在⊙O外 D、无法确定2. 在一个有10万人的小镇,随机调查了1000人,其中有120人周六早上观看中央电视台的“朝闻天下”节目,那么在该镇随便问一个人,他在周六早上观看中央电视台的“朝闻天下”节目的概率大约是( )A、 B、 C、 D、3. 如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 掷一枚质地均匀的硬币,前6次都是正面朝上,则掷第7次时正面朝上的概率是( )A、1 B、 C、 D、05. 如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的大小为( )
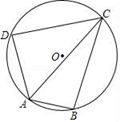
4. 掷一枚质地均匀的硬币,前6次都是正面朝上,则掷第7次时正面朝上的概率是( )A、1 B、 C、 D、05. 如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的大小为( )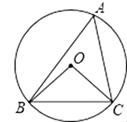 A、40° B、50° C、80° D、100°6. 如图,平面直角坐标系中, 与 轴分别交于 、 两点,点 的坐标为 , .将 沿着与 轴平行的方向平移多少距离时 与 轴相切 ( )
A、40° B、50° C、80° D、100°6. 如图,平面直角坐标系中, 与 轴分别交于 、 两点,点 的坐标为 , .将 沿着与 轴平行的方向平移多少距离时 与 轴相切 ( )
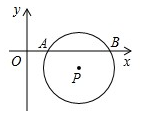
A、1 B、2 C、3 D、1或37.竖直向上发射的小球的高度h(m)关于运动时间t(s)的函数表达式为h=at2+bt,其图象如图所示,若小球在发射后第2秒与第6秒时的高度相等,则下列时刻中小球的高度最高的是( )
 A、第3秒 B、第3.5秒 C、第4.2秒 D、第6.5秒8. 若一个圆锥的底面半径为3cm,母线长为5cm,则这个圆锥的全面积为( )
A、第3秒 B、第3.5秒 C、第4.2秒 D、第6.5秒8. 若一个圆锥的底面半径为3cm,母线长为5cm,则这个圆锥的全面积为( )
A、15π cm2 B、24π cm2 C、39π cm2 D、48π cm2二、填空题
-
9. 已知关于x的函数y=(m﹣1)x2+2x+m图象与坐标轴只有2个交点,则m=.10. 在10个外观相同的产品中,有2个不合格产品,现从中任意抽取1个进行检测,抽到合格产品的概率是 .11. 上午某一时刻,身高1.7米的小刚在地面上的影长为3.4米,则影长26米的旗轩高度为米12. 如图,AB为⊙O的直径,C为⊙O上一点,∠BOC=50°,AD∥OC,AD交⊙O于点D,连接AC,CD,那么∠ACD= .
 13. 如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为 .
13. 如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为 .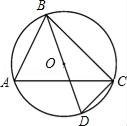 14. 如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是.
14. 如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是.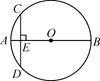 15. 在小于等于9的正整数中任意取出一个数,取到素数的可能性大小是 .16. 如图为二次函数 的图象,下列说法正确的有.
15. 在小于等于9的正整数中任意取出一个数,取到素数的可能性大小是 .16. 如图为二次函数 的图象,下列说法正确的有.① ;② ;③ ④当 时,y随x的增大而增大;⑤方程 的根是 , .

三、综合题
-
17. 已知四边形ABCD是⊙O的内接四边形,∠DAB=120°,BC=CD , AD=4,AC=7,求AB的长度.
 18. 如图,AB是圆锥底面圆的直径,SO是高,OA=3cm , SO=4cm , 求圆锥侧面展开图的面积.
18. 如图,AB是圆锥底面圆的直径,SO是高,OA=3cm , SO=4cm , 求圆锥侧面展开图的面积.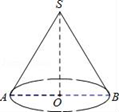 19. 某商店以20元/千克的单价新进一批商品,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间为一次函数关系,如图所示.
19. 某商店以20元/千克的单价新进一批商品,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间为一次函数关系,如图所示. (1)、求y与x的函数表达式;(2)、要使销售利润达到800元,销售单价应定为每千克多少元?20. 某水果公司以2元千克的成本购进1000千克柑橘,销售人员从柑橘中抽取若干柑橘统计损坏情况,结果如下表:
(1)、求y与x的函数表达式;(2)、要使销售利润达到800元,销售单价应定为每千克多少元?20. 某水果公司以2元千克的成本购进1000千克柑橘,销售人员从柑橘中抽取若干柑橘统计损坏情况,结果如下表:柑橘总质量
损坏柑橘质量
柑橘损坏的频率
50
5.5
0.110
100
10.5
0.105
150
15.15
0.101
200
19.42
0.097
250
24.25
0.097
300
30.93
0.130
350
35.32
0.101
400
39.24
0.098
450
44.57
0.099
500
51.42
0.103
(1)、请根据表格中的数据,估计这批柑橘损坏的概率(精确到0.01);(2)、公司希望这批柑橘能够至少获利500元,则毎千克最低定价为多少元?(精确到0.1元).21. 已知二次函数y=2x2+4x+k﹣1. (1)、当二次函数的图象与x轴有交点时,求k的取值范围;(2)、若A(x1 , 0)与B(x2 , 0)是二次函数图象上的两个点,且当x=x1+x2时,y=﹣6,求二次函数的解析式,并在所提供的坐标系中画出大致图象;(3)、在(2)的条件下,将抛物线在x轴下方的部分沿x轴翻折,图象其余部分保持不变,得到一个新的图象,当直线y= x+m(m<3)与新图象有两个公共点,且m为整数时,求m的值.22. 在一个红色不透明的盒子中放有四张分别写有数字1,2,3,4的红色卡片,在一个蓝色不透明的盒子中放有三张分别写有数字1,2,3的蓝色卡片,卡片除颜色和数字外完全相同.(1)、从红盒中任意抽取一张红色卡片,从蓝盒中任意抽取一张蓝色卡片,用列举法(树形图或列表法)表示所有的可能情况;(2)、求两张卡片上写有相同数字的概率.23. 如图,已知AB是⊙O的直径,BC是弦,弦BD平分∠ABC交AC于F , 弦DE⊥AB于H , 交AC于G .
(1)、当二次函数的图象与x轴有交点时,求k的取值范围;(2)、若A(x1 , 0)与B(x2 , 0)是二次函数图象上的两个点,且当x=x1+x2时,y=﹣6,求二次函数的解析式,并在所提供的坐标系中画出大致图象;(3)、在(2)的条件下,将抛物线在x轴下方的部分沿x轴翻折,图象其余部分保持不变,得到一个新的图象,当直线y= x+m(m<3)与新图象有两个公共点,且m为整数时,求m的值.22. 在一个红色不透明的盒子中放有四张分别写有数字1,2,3,4的红色卡片,在一个蓝色不透明的盒子中放有三张分别写有数字1,2,3的蓝色卡片,卡片除颜色和数字外完全相同.(1)、从红盒中任意抽取一张红色卡片,从蓝盒中任意抽取一张蓝色卡片,用列举法(树形图或列表法)表示所有的可能情况;(2)、求两张卡片上写有相同数字的概率.23. 如图,已知AB是⊙O的直径,BC是弦,弦BD平分∠ABC交AC于F , 弦DE⊥AB于H , 交AC于G .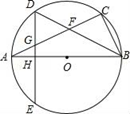 (1)、求证:AG=GD;(2)、当∠ABC满足什么条件时,△DFG是等边三角形?(3)、若AB=10,sin∠ABD= ,求BC的长.24. 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)、求证:AG=GD;(2)、当∠ABC满足什么条件时,△DFG是等边三角形?(3)、若AB=10,sin∠ABD= ,求BC的长.24. 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC. (1)、求证:PA是⊙O的切线;(2)、若AB=4+ ,BC=2 ,求⊙O的半径.25. 如图,直线AB和抛物线的交点是A(0,﹣3),B(5,9),已知抛物线的顶点D的横坐标是2.
(1)、求证:PA是⊙O的切线;(2)、若AB=4+ ,BC=2 ,求⊙O的半径.25. 如图,直线AB和抛物线的交点是A(0,﹣3),B(5,9),已知抛物线的顶点D的横坐标是2.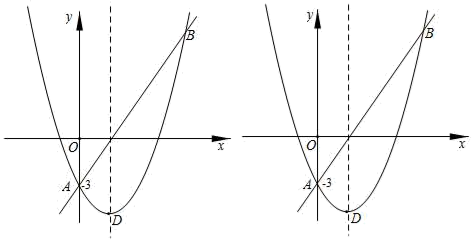 (1)、求抛物线的解析式及顶点坐标;(2)、在x轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不在,请说明理由;(3)、在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.26. 如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从B出发沿BA向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点,点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm,当点Q到达顶点C时,P,Q同时停止运动,设P,Q两点运动时间为t秒.
(1)、求抛物线的解析式及顶点坐标;(2)、在x轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不在,请说明理由;(3)、在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.26. 如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从B出发沿BA向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点,点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm,当点Q到达顶点C时,P,Q同时停止运动,设P,Q两点运动时间为t秒.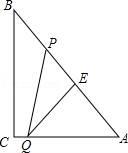 (1)、当t为何值时,PQ∥BC?(2)、设四边形PQCB的面积为y,求y关于t的函数关系式;(3)、四边形PQCB面积能否是△ABC面积的 ?若能,求出此时t的值;若不能,请说明理由;(4)、当t为何值时,△AEQ为等腰三角形?(直接写出结果)
(1)、当t为何值时,PQ∥BC?(2)、设四边形PQCB的面积为y,求y关于t的函数关系式;(3)、四边形PQCB面积能否是△ABC面积的 ?若能,求出此时t的值;若不能,请说明理由;(4)、当t为何值时,△AEQ为等腰三角形?(直接写出结果)