湖南省株洲市芦淞区2019年中考数学一模试卷

试卷更新日期：2020-05-09 类型：中考模拟

进入出卷网下载

一、选择题

1. －5的相反数是（）

A、 $- \frac{1}{5}$ B、 $\frac{1}{5}$ C、5 D、-5

查看试题解析
2. 计算2a²＋3a²的结果是（）

A、5a⁴ B、6a² C、6a⁴ D、5a²

查看试题解析
3. 亚洲陆地面积约为4400万平方千米，将44000000科学记数法表示为（　　）

A、4.4×10⁷ B、4.4×10⁶ C、0.44×10⁷ D、4.4×10³

查看试题解析
4. 下列银行图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 在以下数据75，80，80，85，90中，众数、中位数分别是（　　）

A、75，80 B、80，80 C、80，85 D、80，90

查看试题解析
6. 若 $\sqrt{x + 2}$ 在实数范围内有意义，则x的取值范围在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
7. 如图，在同一平面内，将边长相等的正方形、正五边形的一边重合，那么∠1的大小是（）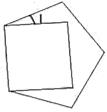

A、 $8^{°}$ B、 $15^{°}$ C、 $18^{°}$ D、 $28^{°}$

查看试题解析
8. 中央电视台2套“开心辞典”栏目中，一期的题目如图所示，两个天平都平衡，则三个球体的重量等于（）个正方体的重量.

A、2 B、3 C、4 D、5

查看试题解析
9. （2015永州）定义[x]为不超过x的最大整数，如[3.6]=3，[0.6]=0，[﹣3.6]=﹣4．对于任意实数x ，下列式子中不正确的是（）

A、[x]=x（x为整数） B、0≤x﹣[x]＜1 C、[x+y]≤[x]+[y] D、[n+x]=n+[x]（n为整数）

查看试题解析
10. 如图，抛物线y=ax²+bx+c（a≠0）过点（1，0）和点（0，﹣2），且顶点在第三象限，设P=a﹣b+c，则P的取值范围是（）

A、﹣4＜P＜0 B、﹣4＜P＜﹣2 C、﹣2＜P＜0 D、﹣1＜P＜0

查看试题解析

二、填空题

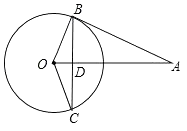
11. 某地某天的最高气温是6℃，最低气温是﹣4℃，则该地当天的温差为℃．

查看试题解析
12. 比较大小：3 $\sqrt{10}$ (填<，>或＝)．

查看试题解析
13. 因式分解： $2 a^{3} - 8 a$ ＝.

查看试题解析
14. 给甲、乙、丙三人打电话，若打电话的顺序是任意的，则第一个打电话给甲的概率是．

查看试题解析
15. 已知反比例函数的解析式为y＝ $\frac{| a | - 2}{x}$ ．则a的取值范围是．

查看试题解析
16. 如图，AB与⊙O相切于点B，线段OA与弦BC垂直，垂足为D，AB=BC=2，则∠AOB=°．

查看试题解析
17. 如图，矩形OABC的顶点A、C分别在坐标轴上，B（8，7），D（5，0），点P是边AB上的一点，连接OP ， DP ，当△ODP为等腰三角形时，点BP的长度为．

查看试题解析
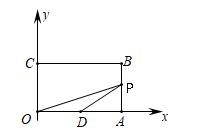18. 如图所示，在平面直角坐标系中，若干个半径为2个单位长度，圆心角为60°的扇形组成一条连续的曲线，点P从原点O出发，沿这条曲线向右上下起伏运动，点在直线上的速度为每秒2个单位长度，点在弧线上的速度为每秒 $\frac{2 π}{3}$ 个单位长度，则第2018秒时，点P的坐标是．

查看试题解析

三、综合题

19. $\sqrt{8}$ ﹣4sin45°﹣2^﹣1

查看试题解析
20. 先化简，再求值：（ $\frac{a + b}{a - b}$ ﹣1）÷ $\frac{b^{2}}{a^{2} - a b}$ ，其中a＝﹣1，b＝ $\sqrt{2}$ ．

查看试题解析
21. 如图，BC是路边坡角为30°，长为10米的一道斜坡，在坡顶灯杆CD的顶端D处有一探射灯，射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°（图中的点A、B、C、D、M、N均在同一平面内，CM∥AN）．

(1)、求灯杆CD的高度；

(2)、求AB的长度（结果精确到0.1米）．（参考数据： $\sqrt{3}$ =1.73．sin37°≈060，cos37°≈0.80，tan37°≈0.75）

查看试题解析

22. 某区在实施居民用水管理前，随机调查了部分家庭（单位：户）去年的月均用水量（单位：t），并将调查数据进行整理，绘制出如下不完整的统计图表：

月均用水量	频数	频率
0≤x＜5	6	12%
5≤x＜10	12	24%
10≤x＜15		32%
15≤x＜20	10	20%
20≤x＜25	4
25≤x＜30	2	4%
合计		100%

请解答以下问题：

(1)、把上面的频数分布表和频数分布直方图补充完整；

(2)、若该小区有2000户家庭，根据此次随机抽查的数据估计，该小区月均用水量不低于20t的家庭有多少户？

(3)、为了鼓励节约用水，要确定一个月均用水量的标准，超出该标准的部分按1.5倍价格收费，若要使68%的家庭水费支出不受影响，那么，你觉得家庭月均用水量应定为多少？

查看试题解析

23. 如图，在正方形ABCD中，E是边CD上一点（点E不与点C ， D重合），连接BE ．取BE的中点M ，过点M作FG⊥BE交BC于点F ，交AD于点G ．

(1)、求证：BE＝FG ．

(2)、连接CM ，若CM＝1，试求FG的长．

查看试题解析
24. 如图，在平面直角坐标系中，一次函数y＝﹣ $\frac{1}{2}$ x+3的图象与反比例函数y＝ $\frac{k}{x}$ （x＞0，k是常数）的图象交于A（a ， 2），B（4，b）两点．

(1)、求反比例函数的表达式；

(2)、点C是第一象限内一点，连接AC ， BC ，使AC∥x轴，BC∥y轴，连接OA ， OB ．若点P在y轴上，且△OPA的面积与四边形OACB的面积相等，求点P的坐标．

查看试题解析
25. 如图，在△ABC中，∠ABC＝90°，以AB的中点O为圆心，OA为半径的圆交AC于点D，E是BC的中点，连接DE，OE．

(1)、判断DE与⊙O的位置关系，并说明理由；

(2)、求证：BC²＝2CD•OE；

(3)、若 $\cos ∠ B A D = \frac{3}{5} ， B E = \frac{14}{3}$ ，求OE的长．

查看试题解析
26. 已知：抛物线y＝x²﹣2（m﹣1）x﹣1﹣m

(1)、当m＝2时，求该抛物线的对称轴和顶点坐标；

(2)、设该抛物线与x轴交于A（x₁ ， 0）、B（x₂ ， 0），x₁＜0＜x₂ ，与y轴交于点C ，且满足 $\frac{1}{A O} - \frac{1}{B O} = \frac{2}{C O}$ ，求这个抛物线的解析式；

(3)、在（2）的条件下，是否存在着直线y＝kx+b与抛物线交于点P、Q ，使y轴平分△CPQ的面积？若存在，求出k ， b应满足的条件；若不存在，请说明理由．

查看试题解析