湖南省株洲市醴陵市2019年中考数学一模试卷

试卷更新日期：2020-05-09 类型：中考模拟

进入出卷网下载

一、选择题

1. |﹣3|＝（）

A、 $\frac{1}{3}$ B、﹣ $\frac{1}{3}$ C、3 D、﹣3

查看试题解析
2. 据国土资源部数据显示，我国是全球“可燃冰”资源储量最多的国家之一，海、陆总储量约为39000000000吨油当量，将39000000000用科学记数法表示为（）

A、3.9×10¹⁰ B、3.9×10⁹ C、0.39×10¹¹ D、39×10⁹

查看试题解析
3. 下列计算正确的是（）

A、3x+2y＝5xy B、（x⁴）³＝x¹² C、（x+y）²＝x²+y² D、2x²÷2x²＝0

查看试题解析
4. 甲、乙两超市在1月至8月间的盈利情况统计图如图所示，下面结论不正确的是（）

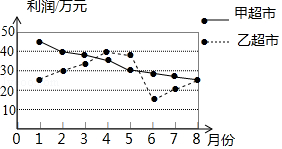A、甲超市的利润逐月减少 B、乙超市的利润在1月至4月间逐月增加 C、8月份两家超市利润相同 D、乙超市在9月份的利润必超过甲超市

查看试题解析
5. 下列说法正确的是（）

A、有两条边和一个角对应相等的两个三角形全等 B、矩形的对角线互相垂直平分 C、正方形既是轴对称图形又是中心对称图形 D、一组对边平行，另一组对边相等的四边形是平行四边形

查看试题解析
6. 解分式方程 $\frac{1}{x - 2}$ ﹣3= $\frac{4}{2 - x}$ 时，去分母可得（）

A、1﹣3（x﹣2）=4 B、1﹣3（x﹣2）=﹣4 C、﹣1﹣3（2﹣x）=﹣4 D、1﹣3（2﹣x）=4

查看试题解析
7. 如图，在⊙O中，CD为⊙O的切线，切点为C，已知∠B＝25°，那么∠D为（）

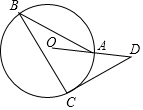A、30° B、40° C、50° D、60°

查看试题解析
8. 下列哪个选项表示的点有可能在反比例函数y＝ $\frac{a^{2} + 1}{x}$ 的图象上（）

A、(﹣1，2) B、(1，﹣2) C、(2，3) D、(2，﹣3)

查看试题解析
9. 如图，已知AB、CD、EF都与BD垂直，垂足分别是B、D、F，且AB＝1，CD＝3，那么EF的长是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{3}{4}$ D、 $\frac{4}{5}$

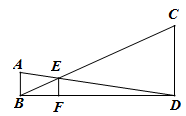查看试题解析
10. 如图，在平面直角坐标系中，点A、B的坐标分别为(1，3)、(n，3)，若直线y＝2x与线段AB有公共点，则n的值可以为（）

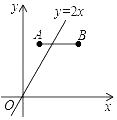A、1 B、1.2 C、1.4 D、1.6

查看试题解析

二、填空题

11. 二次根式 $\sqrt{x - 1}$ 中字母x的取值范围是．

查看试题解析
12. 一组数据：3，8，6，7，6，5的中位数是．

查看试题解析
13. 因式分解：（m²+1）（x﹣y）﹣2m（x﹣y）＝．

查看试题解析
14. 若一个多边形内角和等于1260°，则该多边形边数是．

查看试题解析
15. 古代有个数学问题，意思是“假设有5头牛，2只羊，值金10两；2头牛，5只羊，值金8两．问每头牛、每只羊各值金多少两？”你的答案是每头牛两．

查看试题解析
16. 如图，分别以等边三角形的每个顶点为圆心、以边长为半径在另两个顶点间作一段圆弧，三段圆弧围成的曲边三角形称为勒洛三角形．若等边三角形的边长为9，则勒洛三角形的周长为．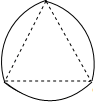

查看试题解析
17. 如图，矩形纸片ABCD中，已知AD=8，折叠纸片使AB边与对角线AC重合，点B落在点F处，折痕为AE，且EF=3，则AB的长为．

查看试题解析
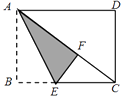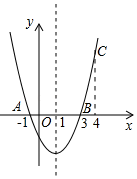
18. 如图，二次函数y＝ax²+bx+c的图象经过点A(﹣1，0)、点B(3，0)、点C(4，y₁)，若点D(x₂ ， y₂)是抛物线上任意一点，有下列结论：
①二次函数y＝ax²+bx+c的最小值为﹣4a；

②若﹣1≤x₂≤4，则0≤y₂≤5a；

③若y₂＞y₁ ，则x₂＞4；

④一元二次方程cx²+bx+a＝0的两个根为﹣1和 $\frac{1}{3}$

其中符合题意结论的是（填序号）．

查看试题解析

三、综合题

19. 计算：2cos30°+（ $\frac{1}{2}$ ）^﹣1﹣ $\sqrt{4}$ +2019⁰

查看试题解析
20. 先化简，再求值：（1﹣ $\frac{1}{x + 2}$ ）÷（x+ $\frac{1}{x + 2}$ ），其中x＝2．

查看试题解析
21. 汽车超速行驶是交通安全的重大隐患，为了有效降低交通事故的发生，许多道路在事故易发路段设置了区间测速，如图新建的醴陵320国道（用直线l表示），进入株洲城区的AB路段设有区间测速，所有车辆限速60千米/小时（约为16.7米/秒），数学实践活动小组设计了如下活动：在l上确定A，B两点，并在AB路段进行区间测速．在l外取一点P，作PC⊥l，垂足为点C．测得PC＝40米，∠APC＝71°，∠BPC＝35°．

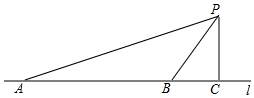(1)、求AB的长；

(2)、若上午9时测得一汽车从点A到点B用时5.5秒，请你用所学的数学知识说明该车是否超速．（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70，sin71°≈0.95，cos71°≈0.33，tan71°≈2.90）

查看试题解析
22. 在“传箴言”活动中，某班团支部对该班全体团员在一个月内所发箴言条数的情况进行了统计，并制成了如图所示的两幅不完整的统计图：

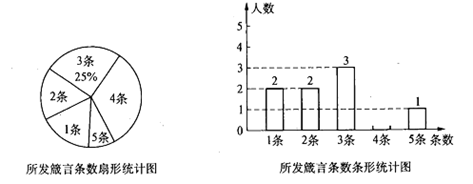(1)、求该班团员在这一个月内所发箴言的平均条数是多少？并将该条形统计图补充完整；

(2)、如果发了3条箴言的同学中有两位男同学，发了4条箴言的同学中有三位女同学.现要从发了3条箴言和4条箴言的同学中分别选出一位参加该校团委组织的“箴言”活动总结会，请你用列表法或树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.

查看试题解析
23. 在Rt△ABC中，∠BAC= 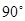，D是BC的中点，E是AD的中点．过点A作AF∥BC交BE的延长线于点F．

(1)、求证：△AEF≌△DEB；

(2)、证明四边形ADCF是菱形；

(3)、若AC=4，AB=5，求菱形ADCFD 的面积．

查看试题解析
24. 如图，直线y＝2x＋6与反比例函数y＝ $\frac{k}{x}$ (k＞0)的图像交于点A(1，m)，与x轴交于点B，平行于x轴的直线y＝n(0＜n＜6)交反比例函数的图象于点M，交AB于点N，连接BM.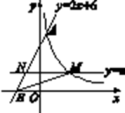

(1)、求m的值和反比例函数的表达式；

(2)、直线y＝n沿y轴方向平移，当n为何值时，△BMN的面积最大？

查看试题解析
25. 如图，AB是⊙O的直径，过点A作⊙O的切线并在其上取一点C，连接OC交⊙O于点D，BD的延长线交AC于E，连接AD，

(1)、求证：CD²＝CE•AC；

(2)、若AB＝4，AC＝4 $\sqrt{2}$ ，求AE的长．

查看试题解析
26. 在平面直角坐标系中，抛物线y＝﹣ $\frac{1}{2}$ x²+ $\frac{3}{2}$ x+m﹣1交x轴于A、B两点，交y轴于点C，若A点坐标为(x₁ ， 0)，B点坐标为(x₂ ， 0)（x₁≠x₂）．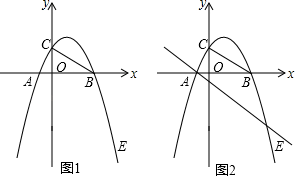

(1)、求m的取值范围；

(2)、如图1，若x₁²+x₂²＝17，求抛物线的解析式；

(3)、在（2）的条件下，请解答下列两个问题：
①如图1，请连接AC，求证：△ACB为直角三角形．

②如图2，若D(1，n)在抛物线上，过点A的直线y＝﹣x﹣1交（2）中的抛物线于点E，那么在x轴上点B的左侧是否存在点P，使以P、B、D为顶点的三角形与△ABE相似？若存在，求出P点坐标；若不存在，说明理由．

查看试题解析