湖南省株洲市荷塘区2019年中考数学一模试卷
试卷更新日期:2020-05-09 类型:中考模拟
一、选择题
-
1. 北京、株洲两个城市在2019年一月份的平均气温分别是﹣4℃、6℃,则2019年一月份株洲市的平均气温比北京市的平均气温高( )A、﹣2℃ B、2℃ C、10℃ D、﹣10℃2.
如图,数轴上有A,B,C,D四个点,其中表示绝对值相等的两个实数的点是( )
 A、点A与点D B、点B 与点D C、点B与点C D、点C与点D3. 若代数式 在实数范围内有意义,则实数x的取值范围是( )A、x>5 B、x=5 C、x≠0 D、x≠54. 一元二次方程2x2﹣3x+1=0的二次项系数是2,则一次项系数是( )A、1 B、﹣3 C、3 D、﹣15. 如图,在2×2网格中放置了三枚棋子,在其他格点处再放置1枚棋子,使图形中的四枚棋子成为轴对称图形的概率是( )
A、点A与点D B、点B 与点D C、点B与点C D、点C与点D3. 若代数式 在实数范围内有意义,则实数x的取值范围是( )A、x>5 B、x=5 C、x≠0 D、x≠54. 一元二次方程2x2﹣3x+1=0的二次项系数是2,则一次项系数是( )A、1 B、﹣3 C、3 D、﹣15. 如图,在2×2网格中放置了三枚棋子,在其他格点处再放置1枚棋子,使图形中的四枚棋子成为轴对称图形的概率是( ) A、 B、 C、 D、6. 如图,AB∥CD,DB⊥BC,∠2=50°,则∠1的度数是( )
A、 B、 C、 D、6. 如图,AB∥CD,DB⊥BC,∠2=50°,则∠1的度数是( )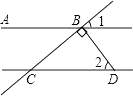 A、40° B、50° C、60° D、140°7. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD是AB边上的中线,则CD的长是( )
A、40° B、50° C、60° D、140°7. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD是AB边上的中线,则CD的长是( ) A、20 B、10 C、5 D、8. 由方程组 ,可得x与y的关系是( )A、 B、 C、 D、9. 如图,平行四边形ABCD中,AB=4,AD=6,∠ABC=60°,∠BAD与∠ABC的平分线AE、BF交于点P,连接PD,则tan∠ADP的值为( )
A、20 B、10 C、5 D、8. 由方程组 ,可得x与y的关系是( )A、 B、 C、 D、9. 如图,平行四边形ABCD中,AB=4,AD=6,∠ABC=60°,∠BAD与∠ABC的平分线AE、BF交于点P,连接PD,则tan∠ADP的值为( ) A、 B、 C、 D、10. 如图,A , B , C三点均在二次函数y=x2的图象上,M为线段AC的中点,BM∥y轴,且MB=2.设A , C两点的横坐标分别为t1、t2(t2>t1),则t2﹣t1的值为( )
A、 B、 C、 D、10. 如图,A , B , C三点均在二次函数y=x2的图象上,M为线段AC的中点,BM∥y轴,且MB=2.设A , C两点的横坐标分别为t1、t2(t2>t1),则t2﹣t1的值为( )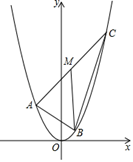 A、3 B、2 C、2 D、2
A、3 B、2 C、2 D、2二、填空题
-
11. 计算 的结果是 .12. 分解因式2a(b+c)-3(b+c)的结果是.13. 某公园划船项目收费标准如下:
船型
两人船
(限乘两人)
四人船
(限乘四人)
六人船
(限乘六人)
八人船
(限乘八人)
每船租金
(元/小时)
90
100
130
150
某班18名同学一起去该公园划船,若每人划船的时间均为1小时,则租船的总费用最低为元.
14. 如图,矩形ABCD的顶点A和对称中心在反比例函数y= (k≠0,x>0)的图象上,若矩形ABCD的面积为16,则k的值为 . 15. 面试时,某应聘者的学历、经验和工作态度的得分分别是75分、80分、85分,若依次按照1:2:2的比例确定成绩,则该应聘者的最终成绩是分.16. 我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度.祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位,其结果领先世界一千多年.“割圆术”的第一步是计算单位圆内正六边形的面积S6 , 则S6= .17. 如图,在平面直角坐标系中,四边形 是正方形,点 的坐标为 ,弧 是以点 为圆心, 为半径的圆弧;弧 是以点 为圆心, 为半径的圆弧,弧 是以点 为圆心, 为半径的圆弧,弧 是以点 为圆心, 为半径的圆弧.继续以点 , , , 为圆心按上述作法得到的曲线 …称为正方形的“渐开线”,则点 的坐标是 .
15. 面试时,某应聘者的学历、经验和工作态度的得分分别是75分、80分、85分,若依次按照1:2:2的比例确定成绩,则该应聘者的最终成绩是分.16. 我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度.祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位,其结果领先世界一千多年.“割圆术”的第一步是计算单位圆内正六边形的面积S6 , 则S6= .17. 如图,在平面直角坐标系中,四边形 是正方形,点 的坐标为 ,弧 是以点 为圆心, 为半径的圆弧;弧 是以点 为圆心, 为半径的圆弧,弧 是以点 为圆心, 为半径的圆弧,弧 是以点 为圆心, 为半径的圆弧.继续以点 , , , 为圆心按上述作法得到的曲线 …称为正方形的“渐开线”,则点 的坐标是 .
三、综合题
-
18. 如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A′处,连接A′C , 则∠BA′C的度数.
 19. 计算:20. 先化简再求值:(a﹣ )÷ ,其中a=1+ ,b=1﹣ .
19. 计算:20. 先化简再求值:(a﹣ )÷ ,其中a=1+ ,b=1﹣ .
21.如图,某翼装飞行员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC(结果精确到1m).
 22. 某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2000名学生的数学成绩进行统计分析,相应数据的统计图表如下:
22. 某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2000名学生的数学成绩进行统计分析,相应数据的统计图表如下:各类学生成绩人数比例统计表
等第
人数
类别
A
B
C
D
农村
200
240
80
县镇
290
132
130
城市
240
132
48
(注:等第A、B、C、D分别代表优秀、良好、合格、不合格)
 (1)、请将上面表格中缺少的三个数据补充完整;(2)、若该市九年级共有15000名学生参加测试,试估计该市学生成绩合格以上(含合格)的人数.23. 已知矩形ABCD中,AB=2,BC=m , 点E是边BC上一点,BE=1,连接AE , 沿AE翻折△ABE使点B落在点F处.
(1)、请将上面表格中缺少的三个数据补充完整;(2)、若该市九年级共有15000名学生参加测试,试估计该市学生成绩合格以上(含合格)的人数.23. 已知矩形ABCD中,AB=2,BC=m , 点E是边BC上一点,BE=1,连接AE , 沿AE翻折△ABE使点B落在点F处.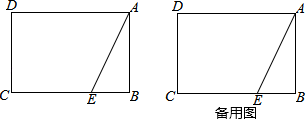 (1)、连接CF , 若CF∥AE , 求m的值;(2)、连接DF , 若 ≤DF≤ ,求m的取值范围.24. 如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF.
(1)、连接CF , 若CF∥AE , 求m的值;(2)、连接DF , 若 ≤DF≤ ,求m的取值范围.24. 如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF.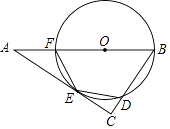 (1)、求证:∠C=90°;(2)、当BC=3,sinA= 时,求AF的长.25. 已知点A(s,t)在反比例函数 (k为常数,k≠0)的图象上.
(1)、求证:∠C=90°;(2)、当BC=3,sinA= 时,求AF的长.25. 已知点A(s,t)在反比例函数 (k为常数,k≠0)的图象上.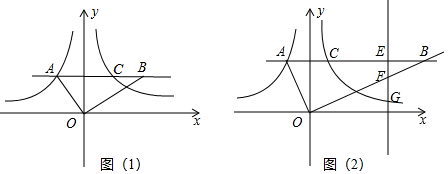 (1)、当s=﹣1,t=3时,则k=;(2)、当点A在第二象限时,将双曲线 (x<0)沿着y轴翻折,翻折后的曲线与原曲线记为曲线L,与过A点的直线y=b(b>0)交于点C,连接AO,过点O作AO的垂线与直线y=b交于点B.
(1)、当s=﹣1,t=3时,则k=;(2)、当点A在第二象限时,将双曲线 (x<0)沿着y轴翻折,翻折后的曲线与原曲线记为曲线L,与过A点的直线y=b(b>0)交于点C,连接AO,过点O作AO的垂线与直线y=b交于点B.①如图(1),当 时,求 值;
②如图(2),若A(﹣1, ),作直线x=n(n>0)交曲线L于G点,分别交射线AB,射线OB于点E,F,当 时,直接写出n的取值范围.
26. 如图,对称轴为直线x=1的抛物线y=x2﹣bx+c与x轴交于A(x1 , 0)、B(x2 , 0)(x1<x2)两点,与y轴交于C点,且 ﹣ .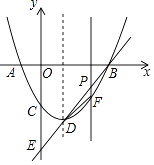 (1)、求抛物线的解析式;(2)、抛物线顶点为D,直线BD交y轴于E点;
(1)、求抛物线的解析式;(2)、抛物线顶点为D,直线BD交y轴于E点;①设点P为线段BD上一点(点P不与B、D两点重合),过点P作x轴的垂线与抛物线交于点F,求△BDF面积的最大值;
②在线段BD上是否存在点Q,使得∠BDC=∠QCE?若存在,求出点Q的坐标;若不存在,请说明理由.