湖南省长沙市天心区明德教育集团2019年中考数学5月模拟试卷
试卷更新日期:2020-05-09 类型:中考模拟
一、选择题
-
1. 下列四个数中,属于无理数的是( )A、 B、- C、0 D、2. 下列图形中,是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 1cm2的电子屏上约有细菌135000个,135000用科学记数法表示为( )A、0.135×106 B、1.35×105 C、13.5×104 D、135×1034. 下列运算正确的是( )A、a3+a3=a6 B、a3•a4=a12 C、a6÷a3=a3 D、(a-b)2=a2-b25. 一个几何体的主视图和俯视图如图所示,则这个几何体可能是( )
3. 1cm2的电子屏上约有细菌135000个,135000用科学记数法表示为( )A、0.135×106 B、1.35×105 C、13.5×104 D、135×1034. 下列运算正确的是( )A、a3+a3=a6 B、a3•a4=a12 C、a6÷a3=a3 D、(a-b)2=a2-b25. 一个几何体的主视图和俯视图如图所示,则这个几何体可能是( ) A、
A、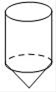 B、
B、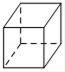 C、
C、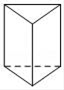 D、
D、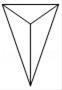 6. 下列性质中菱形不一定具有的性质是( )A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、既是轴对称图形又是中心对称图形7. 把不等式组 的解集表示在数轴上,正确的是( )A、
6. 下列性质中菱形不一定具有的性质是( )A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、既是轴对称图形又是中心对称图形7. 把不等式组 的解集表示在数轴上,正确的是( )A、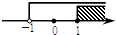 B、
B、 C、
C、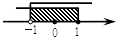 D、
D、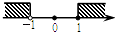 8. 下列说法正确的是( )A、平面内三个点确定一个圆 B、旅客上飞机前的安检应采用抽样调查 C、方差越大,数据的波动越小 D、在标准大气压下,水加热到100℃会沸腾是必然事件9. 甲、乙两船从相距300km的A、B两地同时出发相向而行,甲船从A地顺流航行180km时与从B地逆流航行的乙船相遇,水流的速度为6km/h,若甲、乙两船在静水中的速度均为xkm/h,则求两船在静水中的速度可列方程为( )
8. 下列说法正确的是( )A、平面内三个点确定一个圆 B、旅客上飞机前的安检应采用抽样调查 C、方差越大,数据的波动越小 D、在标准大气压下,水加热到100℃会沸腾是必然事件9. 甲、乙两船从相距300km的A、B两地同时出发相向而行,甲船从A地顺流航行180km时与从B地逆流航行的乙船相遇,水流的速度为6km/h,若甲、乙两船在静水中的速度均为xkm/h,则求两船在静水中的速度可列方程为( )
A、 = B、 = C、 = D、 =10. 如图,在地面上的点A处测得树顶B的仰角为α,AC=7米,则树高BC为(用含α的代数式表示( )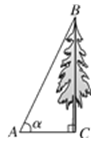 A、7sin 米 B、7cos 米 C、7tan 米 D、 米11. 已知x1、x2是关于x的方程x2﹣ax﹣2=0的两根,下列结论一定正确的是( )A、x1≠x2 B、x1+x2>0 C、x1•x2>0 D、x1<0,x2<012. 二次函数y=ax2+bx﹣2(a≠0)的图象的顶点在第三象限,且过点(1,0),设t=a﹣b﹣2,则t值的变化范围是( )A、﹣2<t<0 B、﹣3<t<0 C、﹣4<t<﹣2 D、﹣4<t<0
A、7sin 米 B、7cos 米 C、7tan 米 D、 米11. 已知x1、x2是关于x的方程x2﹣ax﹣2=0的两根,下列结论一定正确的是( )A、x1≠x2 B、x1+x2>0 C、x1•x2>0 D、x1<0,x2<012. 二次函数y=ax2+bx﹣2(a≠0)的图象的顶点在第三象限,且过点(1,0),设t=a﹣b﹣2,则t值的变化范围是( )A、﹣2<t<0 B、﹣3<t<0 C、﹣4<t<﹣2 D、﹣4<t<0二、填空题
-
13. 因式分解:x3-9x=.14. 函数y= 中,自变量x的取值范围是 .15. 色盲是伴X染色体隐性先天遗传病,患者中男性远多于女性,从男性体检信息库中随机抽取体检表,统计结果如表:
抽取的体检表数n
50
100
200
400
500
800
1000
1200
1500
2000
色盲患者的频数m
3
7
13
29
37
55
69
85
105
138
色盲患者的频率m/n
0.060
0.070
0.065
0.073
0.074
0.069
0.069
0.071
0.070
0.069
根据表中数据,估计在男性中,男性患色盲的概率为 ( 结果精确到0.01).
16. 已知扇形的圆心角为60°,半径为2,则扇形的弧长为(结果保留π).17. 如图,在△ABC中,AC=BC,分别以点A和点C为圆心,大于 长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若∠B=80°,则∠BAD的度数是度.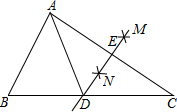 18. 如图,已知第一象限内的点A在反比例函数 上,第二象限的点B在反比例函数 上,且OA⊥OB, ,则k的值为 .
18. 如图,已知第一象限内的点A在反比例函数 上,第二象限的点B在反比例函数 上,且OA⊥OB, ,则k的值为 .
三、综合题
-
19. 计算:20. 先化简,后求值: ,其中x=2018.21. 如图,在平行四边形ABCD中,AD=2AB,CE平分∠BCD,延长CE、BA交于点F,连接AC、DF.
 (1)、如图1,求证:四边形ACDF是平行四边形;(2)、如图2,连接BE,若CF=4 ,tan∠FBE= ,求AE的长.22. 电动自行车已成为市民日常出行的首选工具。据某市品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月销售216辆.(1)、求该品牌电动车销售量的月平均增长率;(2)、若该品牌电动自行车的进价为2300元,售价2800元,则该经销商1月至3月共盈利多少元?23. 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)、如图1,求证:四边形ACDF是平行四边形;(2)、如图2,连接BE,若CF=4 ,tan∠FBE= ,求AE的长.22. 电动自行车已成为市民日常出行的首选工具。据某市品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月销售216辆.(1)、求该品牌电动车销售量的月平均增长率;(2)、若该品牌电动自行车的进价为2300元,售价2800元,则该经销商1月至3月共盈利多少元?23. 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F. (1)、求证:∠ABC=2∠CAF;24. 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过A、B、C三点,已知点A(﹣3,0),B(0,3),C(1,0).
(1)、求证:∠ABC=2∠CAF;24. 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过A、B、C三点,已知点A(﹣3,0),B(0,3),C(1,0).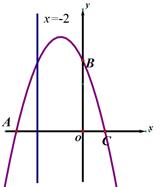
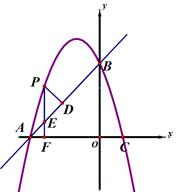 (1)、求此抛物线的解析式;(2)、点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;(3)、在直线 上是否存在点M,使得∠MAC=2∠MCA,若存在,求出M点坐标.若不存在,说明理由.25. 我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)、求此抛物线的解析式;(2)、点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;(3)、在直线 上是否存在点M,使得∠MAC=2∠MCA,若存在,求出M点坐标.若不存在,说明理由.25. 我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.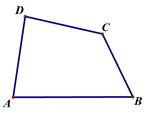
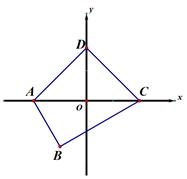 (1)、已知:如图,四边形ABCD是“等对角四边形”, ,则∠C=;(2)、已知:在“等对角四边形”ABCD中,∠DAB=60°,∠ABC=90°,AB=4 , AD=3.求对角线AC的长;(3)、已知:如图,在平面直角坐标系xOy中,四边形ABCD是“等对角四边形”,其中 ,点D在y轴上,抛物线 过点A、C,点P在抛物线上,当满足 的P点至少有3个时,总有不等式 成立,求n 的取值范围.26. 校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图:
(1)、已知:如图,四边形ABCD是“等对角四边形”, ,则∠C=;(2)、已知:在“等对角四边形”ABCD中,∠DAB=60°,∠ABC=90°,AB=4 , AD=3.求对角线AC的长;(3)、已知:如图,在平面直角坐标系xOy中,四边形ABCD是“等对角四边形”,其中 ,点D在y轴上,抛物线 过点A、C,点P在抛物线上,当满足 的P点至少有3个时,总有不等式 成立,求n 的取值范围.26. 校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图: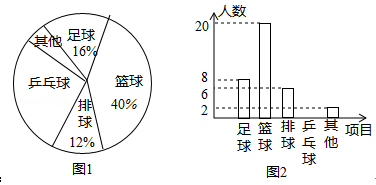
请你根据统计图回答下列问题:
(1)、喜欢乒乓球的学生所占的百分比是多少?并请补全条形统计图;(2)、请你估计全校500名学生中最喜欢“排球”项目的有多少名?(3)、在扇形统计图中,“篮球”部分所对应的圆心角是多少度?(4)、篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.