湖南省永州市零陵区2019年中考数学三模试卷
试卷更新日期:2020-05-09 类型:中考模拟
一、选择题
-
1. 一个数的相反数是 ,则这个数是( )A、2019 B、-2019 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 一个几何体的三视图如图所示,则这个几何体是( )
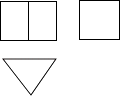 A、圆柱 B、圆锥 C、三棱柱 D、长方体4. 2016年,我国国内生产总值达到74.4万亿元,数据“74.4万亿”用科学记数法表示为( )A、74.4×1012 B、7.44×1013 C、74.4×1013 D、7.44×10155. 据统计,某住宅楼30户居民五月份最后一周每天实行垃圾分类的户数依次是:27,30,29,25,26,28,29,那么这组数据的中位数和众数分别是( )A、25和30 B、25和29 C、28和30 D、28和296. 古代 “绳索量竿”问题:“一条竿子一条索.索比竿子长一托,折回索却量竿,却比竿子短一托.” 其大意为:现有一根竿和一条绳索.用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.则绳索和竿长分别为( )A、30尺和15尺 B、25尺和20尺 C、20尺和15尺 D、15尺和10尺7. 已知等腰三角形的腰和底的长分别是一元二次方程x2-7x+10=0的两个根,则该三角形的周长是( )A、9 B、12 C、9或12 D、不能确定8. 不等式组 的解集在数轴上表示正确的是( )A、
A、圆柱 B、圆锥 C、三棱柱 D、长方体4. 2016年,我国国内生产总值达到74.4万亿元,数据“74.4万亿”用科学记数法表示为( )A、74.4×1012 B、7.44×1013 C、74.4×1013 D、7.44×10155. 据统计,某住宅楼30户居民五月份最后一周每天实行垃圾分类的户数依次是:27,30,29,25,26,28,29,那么这组数据的中位数和众数分别是( )A、25和30 B、25和29 C、28和30 D、28和296. 古代 “绳索量竿”问题:“一条竿子一条索.索比竿子长一托,折回索却量竿,却比竿子短一托.” 其大意为:现有一根竿和一条绳索.用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.则绳索和竿长分别为( )A、30尺和15尺 B、25尺和20尺 C、20尺和15尺 D、15尺和10尺7. 已知等腰三角形的腰和底的长分别是一元二次方程x2-7x+10=0的两个根,则该三角形的周长是( )A、9 B、12 C、9或12 D、不能确定8. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、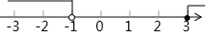 9. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:①abc<0;②b2-4ac>0;③a+b+c>0;④a-b+c>0.其中正确的结论有( )
9. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:①abc<0;②b2-4ac>0;③a+b+c>0;④a-b+c>0.其中正确的结论有( )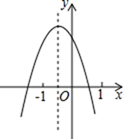 A、1个 B、2个 C、3个 D、4个10. 规定:在平面直角坐标系中,如果点 的坐标为 ,向量 可以用点 的坐标表示为: .已知: , ,如果 ,那么 与 互相垂直.
A、1个 B、2个 C、3个 D、4个10. 规定:在平面直角坐标系中,如果点 的坐标为 ,向量 可以用点 的坐标表示为: .已知: , ,如果 ,那么 与 互相垂直.下列四组向量,互相垂直的是( )
A、 , B、 , C、 , D、 ,二、填空题
-
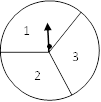
11. 我县某天的最高气温为5℃,最低气温为零下2℃,则温差 .12. 分解因式: = .13. 已知|k+6|+ =0,则一次函数y=kx+b的图象与x轴的交点坐标是 .14. 如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 .
 15. 如图,点A、B、C都在⊙O上,OC⊥OB,点A在劣弧 上,且OA=AB,则∠ABC= .
15. 如图,点A、B、C都在⊙O上,OC⊥OB,点A在劣弧 上,且OA=AB,则∠ABC= .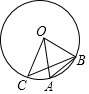 16. 已知圆锥的母线长为10cm , 高为8cm , 则该圆锥的侧面积为cm2 . (结果用π表示)17. 如图,在△ABC中,AD⊥BC于点D , 正方形EFGH的四个顶点都在△ABC的边上,若BC=6cm , AD=4cm , 则正方形EFGH的边长是cm .
16. 已知圆锥的母线长为10cm , 高为8cm , 则该圆锥的侧面积为cm2 . (结果用π表示)17. 如图,在△ABC中,AD⊥BC于点D , 正方形EFGH的四个顶点都在△ABC的边上,若BC=6cm , AD=4cm , 则正方形EFGH的边长是cm .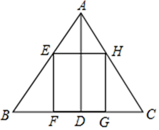 18. 观察下列几组勾股数:3,4,5; 5,12,13; 7,24,25; 9,40,41…按此规律,当直角三角形的最小直角边长是11时,则较长直角边长是;当直角三角形的最小直角边长是 时,则较长直角边长是 .
18. 观察下列几组勾股数:3,4,5; 5,12,13; 7,24,25; 9,40,41…按此规律,当直角三角形的最小直角边长是11时,则较长直角边长是;当直角三角形的最小直角边长是 时,则较长直角边长是 .三、综合题
-
19. 计算: .20. 解方程: .21. 2019年永州市初中体育水平测试进行改革,增加了自选项目,学生可以从篮球运球、足球运球、排球向上垫球三项中必须选一.另外从一分钟跳绳、仰卧起坐(女)或引体向上(男)、原地正面掷实心球、立定跳远中必须选一项.现对永州市某校的选考项目情况进行调查,对调查结果进行了分析统计并制作了两幅统计图:
项目
篮球
足球
排球
性别
男
女
男
女
男
女
人数
30
10
24
12
6
28
平均得分
8
7
8.5
6
9
10
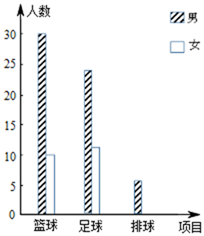 (1)、补全条形统计图;(2)、求抽查的这些男生的体育测试平均分;(3)、若该校准备从这次体育测试成绩好的学生中选出10名参加全市运动会.现在有19名学生报名,小明是这19名同学之一,小明在知道自己这次成绩后还需知道这19名学生成绩的 , 就能知道自己能不能参加市运动会.
(1)、补全条形统计图;(2)、求抽查的这些男生的体育测试平均分;(3)、若该校准备从这次体育测试成绩好的学生中选出10名参加全市运动会.现在有19名学生报名,小明是这19名同学之一,小明在知道自己这次成绩后还需知道这19名学生成绩的 , 就能知道自己能不能参加市运动会.A . 平均数 B . 众数 C . 中位数 D . 方差
22. 如图,在正方形ABCD中,E是对角线BD上一点,连接AE,CE.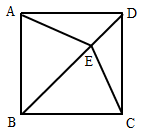 (1)、求证:AE=CE;(2)、若BC= ,BE=6,求tan∠BAE的值.23. 某种商品的标价为500元/件,经过两次降价后的价格为405元/件,并且两次降价的百分率相同.(1)、求该种商品每次降价的百分率;(2)、若该种商品进价为400元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3200元.问第一次降价后至少要售出该种商品多少件?24. 在Rt△ABC中,∠ACB=90°,BE平分∠ABC , D是边AB上一点,以BD为直径的⊙O经过点E , 且交BC于点F .
(1)、求证:AE=CE;(2)、若BC= ,BE=6,求tan∠BAE的值.23. 某种商品的标价为500元/件,经过两次降价后的价格为405元/件,并且两次降价的百分率相同.(1)、求该种商品每次降价的百分率;(2)、若该种商品进价为400元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3200元.问第一次降价后至少要售出该种商品多少件?24. 在Rt△ABC中,∠ACB=90°,BE平分∠ABC , D是边AB上一点,以BD为直径的⊙O经过点E , 且交BC于点F .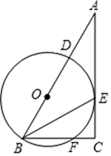 (1)、求证:AC是⊙O的切线;(2)、若BF=12,⊙O的半径为10,求CE的长.25. 定义:若一次函数y=ax+b和反比例函数y=- 满足a+c=2b , 则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数.(1)、判断y=x+b和y=- 是否存在“等差”函数?若存在,写出它们的“等差”函数;(2)、若y=5x+b和y=- 存在“等差”函数,且“等差”函数的图象与y=- 的图象的一个交点的横坐标为1,求一次函数和反比例函数的表达式;(3)、若一次函数y=ax+b和反比例函数y=- (其中a>0,c>0,a= b)存在“等差”函数,且y=ax+b与“等差”函数有两个交点A(x1 , y1)、B(x2 , y2),试判断“等差”函数图象上是否存在一点P(x , y)(其中x1<x<x2),使得△ABP的面积最大?若存在,用c表示△ABP的面积的最大值;若不存在,请说明理由.26. 在菱形ABCD中,∠A=60°,AB=8cm,如图①,点E,H从点A开始向B,D运动,同时点F,G从点C向B,D运动,运动速度都为1cm/秒,运动时间为t秒(0≤t<8).
(1)、求证:AC是⊙O的切线;(2)、若BF=12,⊙O的半径为10,求CE的长.25. 定义:若一次函数y=ax+b和反比例函数y=- 满足a+c=2b , 则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数.(1)、判断y=x+b和y=- 是否存在“等差”函数?若存在,写出它们的“等差”函数;(2)、若y=5x+b和y=- 存在“等差”函数,且“等差”函数的图象与y=- 的图象的一个交点的横坐标为1,求一次函数和反比例函数的表达式;(3)、若一次函数y=ax+b和反比例函数y=- (其中a>0,c>0,a= b)存在“等差”函数,且y=ax+b与“等差”函数有两个交点A(x1 , y1)、B(x2 , y2),试判断“等差”函数图象上是否存在一点P(x , y)(其中x1<x<x2),使得△ABP的面积最大?若存在,用c表示△ABP的面积的最大值;若不存在,请说明理由.26. 在菱形ABCD中,∠A=60°,AB=8cm,如图①,点E,H从点A开始向B,D运动,同时点F,G从点C向B,D运动,运动速度都为1cm/秒,运动时间为t秒(0≤t<8).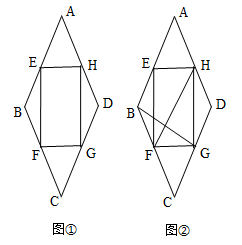 (1)、当运动时间t=4时,求证:四边形EFGH为矩形;(2)、当t等于多少秒时,四边形EFGH面积是菱形ABCD面积的 ;(3)、如图②,连接HF,BG , 当t等于多少秒时,HF⊥BG.
(1)、当运动时间t=4时,求证:四边形EFGH为矩形;(2)、当t等于多少秒时,四边形EFGH面积是菱形ABCD面积的 ;(3)、如图②,连接HF,BG , 当t等于多少秒时,HF⊥BG.