湖南省益阳市资阳区2019年中考数学一模试卷
试卷更新日期:2020-05-09 类型:中考模拟
一、选择题
-
1. 下列四个数中最小的数是( )A、0 B、 C、 D、2. 下列计算正确的是( )A、2a+3b=5ab B、 =±6 C、a6÷a2=a4 D、(2ab2)3=6a3b53. 不等式组 的解集在数轴上表示正确的是( )A、
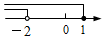 B、
B、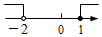 C、
C、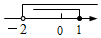 D、
D、 4.
4.如图,几何体的俯视图是( )
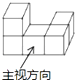 A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,直线 , ,则c与b相交所形成的 度数为( )
5. 如图,直线 , ,则c与b相交所形成的 度数为( )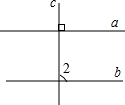 A、 B、 C、 D、6. 某学校在开展“节约每一滴水”的活动中,从九年级的500名同学中任选出10名同学汇报了各自家庭一个月的节水情况,将有关数据整理如下表所示:
A、 B、 C、 D、6. 某学校在开展“节约每一滴水”的活动中,从九年级的500名同学中任选出10名同学汇报了各自家庭一个月的节水情况,将有关数据整理如下表所示:节水量(单位:t)
0.5
1
1.5
2
同学数(人)
2
3
4
1
请你估计这500名同学的家庭一个月节约的水总量大约是( )
A、400t B、500t C、700t D、600t7. 某特快列车在最近一次的铁路大提速后,时速提高了30千米/小时,则该列车行驶350千米所用的时间比原来少用1小时,若该列车提速前的速度是x千米/小时,下列所列方程正确的是( )A、 B、 C、 D、8. 在下列网格中,小正方形的边长为1,点A,B,O都在格点上,则∠A的正弦值是( ) A、 B、 C、 D、9. 如图,DE是边长为2的菱形ABCD的高, ,以点D为圆心,DE的长为半径画弧,交BD于F , 交DC于G , 则图中阴影部分的面积为( )
A、 B、 C、 D、9. 如图,DE是边长为2的菱形ABCD的高, ,以点D为圆心,DE的长为半径画弧,交BD于F , 交DC于G , 则图中阴影部分的面积为( ) A、 B、 C、 D、10. 二次函数 的图象如图所示,则下列结论: ; ; ; 中,正确的结论的个数是( )
A、 B、 C、 D、10. 二次函数 的图象如图所示,则下列结论: ; ; ; 中,正确的结论的个数是( )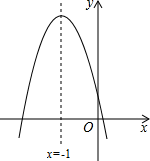 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
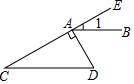
11. 把 化成最简二次根式为 .12. 分解因式:2x2+4xy+2y2= .13. 下列事件中,①打开电视,它正在播关于扬州特产的广告;②太阳绕着地球转;③掷一枚正方体骰子,点数“4”朝上;④13人中至少有2人的生日是同一个月.属于随机事件的个数是 .14. 若函数 是反比例函数,则 .15. 如图,DA⊥CE于点A,CD∥AB,∠1=30°,则∠D= .
 16. 如图,矩形ABCD中,AE平分 交BC于E , ,则下列结论: 是等边三角形; ; ; ,其中正确的结论的序号是 .
16. 如图,矩形ABCD中,AE平分 交BC于E , ,则下列结论: 是等边三角形; ; ; ,其中正确的结论的序号是 .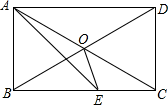 17. 某种商品的进价为15元,出售时标价是22.5元.由于市场不景气销售情况不好,商店准备降价处理,但要保证利润率不低于10%,那么该店最多降价元出售该商品.18. 如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB的度数为.
17. 某种商品的进价为15元,出售时标价是22.5元.由于市场不景气销售情况不好,商店准备降价处理,但要保证利润率不低于10%,那么该店最多降价元出售该商品.18. 如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB的度数为.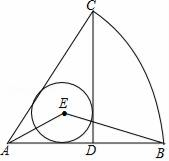
三、综合题
-
19. 计算:(π﹣2019)0+6sin60°﹣|5﹣ |﹣( )﹣220. 先化简,再求值: ,其中 .21. 如图,四边形ABCD中, , ,BD平分 求证:
 (1)、 ;(2)、 .22. 2018年9月,振华中学举行了迎国庆中华传统文化节活动.本次文化节共有五个活动:A﹣书法比赛;B﹣国画竞技;C﹣诗歌朗诵;D﹣汉字大赛;E﹣古典乐器演奏.活动结束后,某班数学兴趣小组开展了“我最喜爱的活动”的抽样调查(每人只选一项),根据收集的数据绘制了两幅不完整的统计图,请根据图中信息,解答下列问题:
(1)、 ;(2)、 .22. 2018年9月,振华中学举行了迎国庆中华传统文化节活动.本次文化节共有五个活动:A﹣书法比赛;B﹣国画竞技;C﹣诗歌朗诵;D﹣汉字大赛;E﹣古典乐器演奏.活动结束后,某班数学兴趣小组开展了“我最喜爱的活动”的抽样调查(每人只选一项),根据收集的数据绘制了两幅不完整的统计图,请根据图中信息,解答下列问题: (1)、此次随机抽取的初三学生共人,m= , 并补全条形统计图;(2)、初三年级准备在五名优秀的书法比赛选手中任意选择两人参加学校的最终决赛,这五名选手中有三名男生和两名女生,用树状图或列表法求选出的两名选手正好是一男一女的概率是多少.23. 反比例函数 (k为常数,且k≠0)的图象经过点A(1,4)、(4,m).
(1)、此次随机抽取的初三学生共人,m= , 并补全条形统计图;(2)、初三年级准备在五名优秀的书法比赛选手中任意选择两人参加学校的最终决赛,这五名选手中有三名男生和两名女生,用树状图或列表法求选出的两名选手正好是一男一女的概率是多少.23. 反比例函数 (k为常数,且k≠0)的图象经过点A(1,4)、(4,m). (1)、求反比例函数的解析式及B点的坐标;(2)、在x轴上找一点P , 使PA+PB的值最小,求满足条件的点P的坐标.24. 某商场销售A、B两种品牌的教学设备,其进价分别为 万元 套, 万元 套;售价分别为 万元 套、 万元 套.该商场计划购进两种教学设备各若干套,共需66万元,全部销售后可获毛利润9万元.(1)、设该商场计划购进A、B两种品牌的教学设备各x套、y套,求x , y的值.(2)、调研后,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的 倍,采购进资金不超过69万元,问A种设备购进量至多减少多少套?25. 如图, 和 是有公共顶点的直角三角形, ,点P为射线BD , CE的交点.
(1)、求反比例函数的解析式及B点的坐标;(2)、在x轴上找一点P , 使PA+PB的值最小,求满足条件的点P的坐标.24. 某商场销售A、B两种品牌的教学设备,其进价分别为 万元 套, 万元 套;售价分别为 万元 套、 万元 套.该商场计划购进两种教学设备各若干套,共需66万元,全部销售后可获毛利润9万元.(1)、设该商场计划购进A、B两种品牌的教学设备各x套、y套,求x , y的值.(2)、调研后,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的 倍,采购进资金不超过69万元,问A种设备购进量至多减少多少套?25. 如图, 和 是有公共顶点的直角三角形, ,点P为射线BD , CE的交点.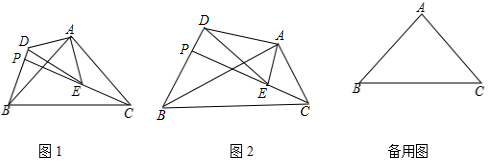 (1)、如图1,若 和 是等腰三角形,求证: ;(2)、如图2,若 ,问:(1)中的结论是否成立?请说明理由.(3)、在(1)的条件下,若 , ,若把 绕点A旋转,当 时,求PB的长.26. 在平面直角坐标系xOy中,将抛物线y=﹣x2平移后经过点A(﹣1,0)、B(4,0),且平移后的抛物线与y轴交于点C(如图).
(1)、如图1,若 和 是等腰三角形,求证: ;(2)、如图2,若 ,问:(1)中的结论是否成立?请说明理由.(3)、在(1)的条件下,若 , ,若把 绕点A旋转,当 时,求PB的长.26. 在平面直角坐标系xOy中,将抛物线y=﹣x2平移后经过点A(﹣1,0)、B(4,0),且平移后的抛物线与y轴交于点C(如图). (1)、求平移后的抛物线的表达式;(2)、如果点D在线段CB上,且CD= ,求∠CAD的正弦值;(3)、点E在y轴上且位于点C的上方,点P在直线BC上,点Q在平移后的抛物线上,如果四边形ECPQ是菱形,求点Q的坐标.
(1)、求平移后的抛物线的表达式;(2)、如果点D在线段CB上,且CD= ,求∠CAD的正弦值;(3)、点E在y轴上且位于点C的上方,点P在直线BC上,点Q在平移后的抛物线上,如果四边形ECPQ是菱形,求点Q的坐标.