湖南省澧县2019年中考数学四模考试试卷
试卷更新日期:2020-05-09 类型:中考模拟
一、选择题
-
1. ﹣ 的绝对值是( )A、﹣ B、 C、﹣2 D、22. 若一个三角形三个内角度数的比为2︰7︰4,那么这个三角形是( )A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形3. 自2013年10月习近平总书记提出“精准扶贫”的重要思想以来.各地积极推进精准扶贫,加大帮扶力度.全国脱贫人口数不断增加.仅2017年我国减少的贫困人口就接近1100万人.将1100万人用科学记数法表示为( )
A、1.1×103人 B、1.1×107人 C、1.1×108人 D、11×106人4. 如图所示的正六棱柱的主视图是( )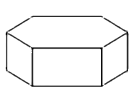 A、
A、 B、
B、 C、
C、 D、
D、 5. 下列判断正确的是( )A、任意掷一枚质地均匀的硬币10次,一定有5次正面向上 B、天气预报说“明天的降水概率为40%”,表示明天有40%的时间都在降雨 C、“篮球队员在罚球线上投篮一次,投中”为随机事件 D、“a是实数,|a|≥0”是不可能事件6. 如图,在 中,延长 至 使得 ,过 中点 作 (点 位于点 右侧),且 ,连接 .若 ,则 的长为( )
5. 下列判断正确的是( )A、任意掷一枚质地均匀的硬币10次,一定有5次正面向上 B、天气预报说“明天的降水概率为40%”,表示明天有40%的时间都在降雨 C、“篮球队员在罚球线上投篮一次,投中”为随机事件 D、“a是实数,|a|≥0”是不可能事件6. 如图,在 中,延长 至 使得 ,过 中点 作 (点 位于点 右侧),且 ,连接 .若 ,则 的长为( ) A、 B、 C、 D、7. 已知点P(a,m),点Q(b,n)都在反比例函数y= 的图像上,且a<0<b,则下列结论一定正确的是( )A、m+n<0 B、m+n>0 C、m<n D、m>n8. 观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2019个图形共有( )个〇.
A、 B、 C、 D、7. 已知点P(a,m),点Q(b,n)都在反比例函数y= 的图像上,且a<0<b,则下列结论一定正确的是( )A、m+n<0 B、m+n>0 C、m<n D、m>n8. 观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2019个图形共有( )个〇.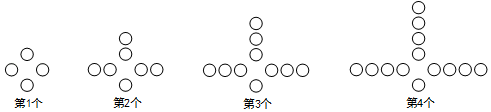 A、6055 B、6056 C、6057 D、6058
A、6055 B、6056 C、6057 D、6058二、填空题
-
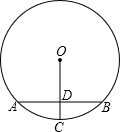
9. 已知 是整数,则正整数n的最小值为10. 分解因式11. 一组数据3,2,3,4,x的平均数是3,则它的方差是 .12. 分式方程 =4的解是x= .13. 如图,AB是⊙O的弦,⊙O的半径OC⊥AB于点D , 若AB=6cm , OD=4cm , 则⊙O的半径为cm .
 14.
14.放学后,小明骑车回家,他经过的路程s(千米)与所用时间t(分钟)的函数关系如图所示,则小明的骑车速度是 千米/分钟.
 15. 如图, 中, , 于 点, 于点 , 于点 , ,则 .
15. 如图, 中, , 于 点, 于点 , 于点 , ,则 .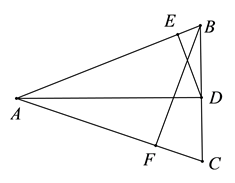 16. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳记数”.如图,一位妇女在从右到左依次排列的绳子上打结,满六进一,用来记录采集到的野果数量,由图可知,她一共采集到的野果数量为个.
16. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳记数”.如图,一位妇女在从右到左依次排列的绳子上打结,满六进一,用来记录采集到的野果数量,由图可知,她一共采集到的野果数量为个.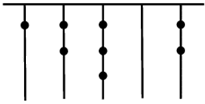
三、综合题
-
17. 计算:18. 解不等式组: ,并把解集在数轴上表示出来.
 19. 先化简,再求值:(1+ )÷ ,其中x满足x2﹣2x﹣5=0.20. 如图,已知一次函数y=kx+b(k≠0)与反比例函数y= (m≠0)的图象相交于A、B两点,且点A的坐标是(1,2),点B的坐标是(﹣2,w).
19. 先化简,再求值:(1+ )÷ ,其中x满足x2﹣2x﹣5=0.20. 如图,已知一次函数y=kx+b(k≠0)与反比例函数y= (m≠0)的图象相交于A、B两点,且点A的坐标是(1,2),点B的坐标是(﹣2,w). (1)、求一次函数与反比例函数的解析式;(2)、在x轴的正半轴上找一点C , 使△AOC的面积等于△ABO的面积,并求出点C的坐标.21. 随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)、求一次函数与反比例函数的解析式;(2)、在x轴的正半轴上找一点C , 使△AOC的面积等于△ABO的面积,并求出点C的坐标.21. 随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: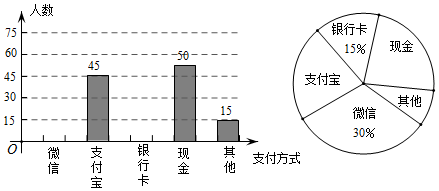 (1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;(2)、将条形统计图补充完整.观察此图,支付方式的“众数”是“”;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.22. 我市在创建全国文明城市的过程中,某社区在甲楼的A处与E处之间悬挂了一副宣传条幅,在乙楼顶部C点测得条幅顶端A点的仰角为45°,条幅底端E点的俯角为30°,若甲、乙两楼之间的水平距离BD为12米,求条幅AE的长度.(结果保留根号)
(1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;(2)、将条形统计图补充完整.观察此图,支付方式的“众数”是“”;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.22. 我市在创建全国文明城市的过程中,某社区在甲楼的A处与E处之间悬挂了一副宣传条幅,在乙楼顶部C点测得条幅顶端A点的仰角为45°,条幅底端E点的俯角为30°,若甲、乙两楼之间的水平距离BD为12米,求条幅AE的长度.(结果保留根号) 23. 第36届全国信息学冬令营在广州落下帷幕,长郡师生闪耀各大赛场,金牌数、奖牌数均稳居湖南省第一.学校拟预算7700元全部用于购买甲、乙、丙三种图书共20套奖励获奖师生,其中甲种图书每套500元,乙种图书每套400元,丙种图书每套250元,设购买甲种图书x套,乙种图书y套,请解答下列问题:(1)、请求出y与x的函数关系式(不需要写出自变量的取值范围);(2)、若学校购买的甲、乙两种图书共14套,求甲、乙图书各多少套?(3)、若学校购买的甲、乙两种图书均不少于1套,则有哪几种购买方案?24. 如图,在⊙O中,半径OC垂直于弦AB , 垂足为点D , 点E在OC的延长线上,∠EAC=∠BAC
23. 第36届全国信息学冬令营在广州落下帷幕,长郡师生闪耀各大赛场,金牌数、奖牌数均稳居湖南省第一.学校拟预算7700元全部用于购买甲、乙、丙三种图书共20套奖励获奖师生,其中甲种图书每套500元,乙种图书每套400元,丙种图书每套250元,设购买甲种图书x套,乙种图书y套,请解答下列问题:(1)、请求出y与x的函数关系式(不需要写出自变量的取值范围);(2)、若学校购买的甲、乙两种图书共14套,求甲、乙图书各多少套?(3)、若学校购买的甲、乙两种图书均不少于1套,则有哪几种购买方案?24. 如图,在⊙O中,半径OC垂直于弦AB , 垂足为点D , 点E在OC的延长线上,∠EAC=∠BAC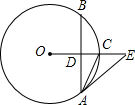 (1)、求证:AE是⊙O的切线;(2)、若AB=8,cosE= ,求CD的长.25. 已知:如图①,将 的菱形 沿对角线 剪开,将 沿射线 方向平移,得到 点 为边 上一点(点 不与点 、点 重合),将射线 绕点 逆时针旋转 ,与 的延长线交于点 ,连接 .
(1)、求证:AE是⊙O的切线;(2)、若AB=8,cosE= ,求CD的长.25. 已知:如图①,将 的菱形 沿对角线 剪开,将 沿射线 方向平移,得到 点 为边 上一点(点 不与点 、点 重合),将射线 绕点 逆时针旋转 ,与 的延长线交于点 ,连接 . (1)、①求证: ;
(1)、①求证: ;②探究 的形状;
(2)、如图②,若菱形 变为正方形 ,将射线 绕点 逆时针旋转 ,原题其他条件不变, 中的①和②两个结论是否仍然成立?若成立,请直接写出结论;若不成立,请写出变化后的结论并证明.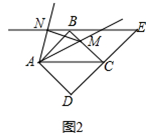 26. 已知抛物线 经过点 ,与 轴交于 两点
26. 已知抛物线 经过点 ,与 轴交于 两点
 (1)、求抛物线 的解析式;(2)、如图1,直线 交抛物线 于 两点, 为抛物线 上 之间的动点,过 点作 轴于点 于点 ,求 的最大值;(3)、如图2,平移抛物线 的顶点到原点得抛物线 ,直线 交抛物线 于 、 两点,在抛物线 上存在一个定点 ,使 ,求点 的坐标.
(1)、求抛物线 的解析式;(2)、如图1,直线 交抛物线 于 两点, 为抛物线 上 之间的动点,过 点作 轴于点 于点 ,求 的最大值;(3)、如图2,平移抛物线 的顶点到原点得抛物线 ,直线 交抛物线 于 、 两点,在抛物线 上存在一个定点 ,使 ,求点 的坐标.