湖南省怀化市洪江市2019年中考数学5月模拟考试试卷

试卷更新日期：2020-05-09 类型：中考模拟

进入出卷网下载

一、选择题

1. 我国南海海域面积为3 500 000 km² ，用科学记数法表示正确的是（）

A、 $3.5 \times 10^{5} k m^{2}$ B、 $3.5 \times 10^{6} k m^{2}$ C、 $3.5 \times 10^{7} k m^{2}$ D、 $3.5 \times 10^{8} k m^{2}$

查看试题解析
2. 将一直角三角板与两边平行的纸条如图放置．已知∠1=30°，则∠2的度数为（）

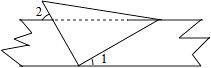A、30° B、45° C、50° D、60°

查看试题解析
3. 多项式ax²﹣4ax﹣12a因式分解正确的是（）

A、a（x﹣6）（x+2） B、a（x﹣3）（x+4） C、a（x²﹣4x﹣12） D、a（x+6）（x﹣2）

查看试题解析
4. 下列几何体中，主视图是圆的是（）

A、圆柱 B、圆锥 C、球 D、立方体

查看试题解析
5. 如图，已知等腰梯形ABCD中，AD∥BC ， AB＝DC ， AC与BD相交于点O ，则下列判断不正确的是（）

A、△ABC≌△DCB B、△AOD≌△COB C、△ABO≌△DCO D、△ADB≌△DAC

查看试题解析
6. 不等式组 ${\begin{array}{l} 4 x - 1 < 7 \\ 2 x + 3 \geq 1 \end{array}$ 的解集是（）

A、﹣1≤x＜2 B、x≥﹣1 C、x＜2 D、﹣1＜x≤2

查看试题解析
7. 如图，D ， E分别是△ABC边AB ， AC的中点，则△ADE与△ABC的面积比为（）

A、1：2 B、1：4 C、2：1 D、4：1

查看试题解析
8. 分式方程 $\frac{3}{x + 2} = \frac{- 1}{x - 2}$ 的解为（）

A、x＝0 B、x＝1 C、x＝﹣1 D、x＝2

查看试题解析
9. 某中学随机调查了15名学生，了解他们一周在校参加体育锻炼的时间，列表如下：

锻炼时间（小时）

5

6

7

8

人数

2

6

5

2

则这15名同学一周在校参加体育锻炼的时间的中位数和众数分别为（）

A、6，7 B、7，7 C、7，6 D、6，6

查看试题解析
10. 已知一次函数y=kx+b的图象如图，那么正比例函数y=kx和反比例函数y= $\frac{b}{x}$ 在同一坐标系中的图象的形状大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 如图，小明爬一土坡，他从A处爬到B处所走的直线距离AB=4米，此时，他离地面高度为h=2米，则这个土坡的坡角∠A=°.

查看试题解析
12. 若点A（﹣2，4）在反比例函数 $y = \frac{k}{x}$ 的图像上，则k的值是．

查看试题解析
13. 如图，在△ABC中，∠A＝30°，∠B＝50°，延长BC到点D，则∠ACD＝°.

查看试题解析
14.
某校九年级有560名学生参加了市教育局举行的读书活动，现随机调查了70名学生读书的数量，根据所得数据绘制了如图的条形统计图，请估计该校九年级学生在此次读书活动中共读书本．

查看试题解析
15. 如图，在正方形 $A B C D$ 的外侧，作等边 $△ D C E$ ，则 $∠ A E C$ 的度数是．

查看试题解析
16. 我们规定：当k，b为常数，k≠0，b≠0，k≠b时，一次函数y=kx+b与y=bx+k互为交换函数．例如：y=4x+3的交换函数为y=3x+4．一次函数y=kx+2与它的交换函数图象的交点横坐标为．

查看试题解析

三、综合题

17. 计算： $| - 3 | - \sqrt{8} - {(π - 2019)}^{0} + 4 s i n 45^{0}$ ．

查看试题解析
18. 设一次函数y=kx+b（k≠0）的图象经过A（1，3），B（0，－2）两点，试求k，b的值．

查看试题解析
19. 如图，在平行四边形ABCD中，∠B=∠AFE，EA是∠BEF的平分线，求证：

(1)、△ABE≌△AFE；

(2)、∠FAD=∠CDE.

查看试题解析
20. 甲乙两名同学做摸球游戏，他们把三个分别标有1，2，3的大小和形状完全相同的小球放在一个不透明的口袋中.

(1)、求从袋中随机摸出一球，标号是1的概率；

(2)、从袋中随机摸出一球后放回，摇匀后再随机摸出一球，若两次摸出的球的标号之和为偶数时，则甲胜；若两次摸出的球的标号之和为奇数时，则乙胜；试分析这个游戏是否公平？请说明理由.

查看试题解析
21. 两个城镇A、B与两条公路ME、MF位置如图所示，其中ME是东西方向的公路．现电信部门需在C处修建一座信号发射塔，要求发射塔到两个城镇A、B的距离相等，到两条公路ME、MF的距离也必须相等，且在∠FME的内部．

(1)、那么点C应选在何处？请在图中，用尺规作图找出符合条件的点C（不写已知、求作、作法，只保留作图痕迹）；

(2)、设AB的垂直平分线交ME于点N，且 $M N = 2 (\sqrt{3} + 1)$ km，在M处测得点C位于点M的北偏东60°方向，在N处测得点C位于点N的北偏西45°方向，求点C到公路ME的距离．

查看试题解析
22. 如图，E是长方形ABCD的边AB上的点，EF⊥DE交BC于点F

(1)、求证：△ADE∽△BEF；

(2)、设H是ED上一点，以EH为直径作⊙O ， DF与⊙O相切于点G ，若DH＝OH＝3，求图中阴影部分的面积（结果保留到小数点后面第一位， $\sqrt{3}$ ≈1.73，π≈3.14）．

查看试题解析
23. 设m是不小于﹣1的实数，使得关于x的方程x²+2（m﹣2）x+m²﹣3m+3=0有两个不相等的实数根x₁ ， x₂ ．

(1)、若 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = 1$ ，求 $\frac{1}{3 - 2 m}$ 的值；

(2)、求 $y = {\begin{cases} - x + 14 (2 \leq x \leq 8) \\ 6 (x > 8) \end{cases}$ 的最大值．

查看试题解析
24. 如图1，在平面直角坐标系中，AB＝OB＝8，∠ABO＝90°，∠yOC＝45°，射线OC以每秒2个单位长度的速度向右平行移动，当射线OC经过点B时停止运动，设平行移动x秒后，射线OC扫过Rt△ABO的面积为y ．

(1)、求y与x之间的函数关系式；

(2)、当x＝3秒时，射线OC平行移动到O′C′，与OA相交于G ，如图2，求经过G ， O ， B三点的抛物线的解析式；

(3)、现有一动点P在（2）中的抛物线上，试问点P在运动过程中，是否存在△POB的面积S＝8的情况？若存在，求出点P的坐标，若不存在，请说明理由．

查看试题解析

锻炼时间（小时）	5	6	7	8
人数	2	6	5	2