四川省绵阳市2020年中考数学一模考试试卷

试卷更新日期：2020-05-06 类型：中考模拟

进入出卷网下载

一、选择题

1. 已知a＜b，则化简二次根式 $\sqrt{- a^{3} b}$ 的正确结果是（）

A、 $- a \sqrt{- a b}$ B、 $- a \sqrt{a b}$ C、 $a \sqrt{a b}$ D、 $a \sqrt{- a b}$

查看试题解析
2. 如图所示，电路图上有A，B，C三个开关和一个小灯泡，闭合开关C或者同时闭合开关A、B，都可使小灯泡发光．现在任意闭合其中一个开关，则小灯泡发光的概率等于（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
3. 四个小朋友站成一排，老师按图中所示的规则数数，数到2019时对应的小朋友可得一朵红花．那么得红花的小朋友是（）

A、小沈 B、小叶 C、小李 D、小王

查看试题解析
4. 如图⊙O的直径 $A B$ 垂直于弦 $C D$ ，垂足是 $E$ ， $∠ A = 22.5 °$ ， $O C = 4$ ， $C D$ 的长为（）

A、 B、4 C、 D、8

查看试题解析
5. 如图，要测量B点到河岸AD的距离，在A点测得∠BAD＝30°，在C点测得∠BCD＝60°，又测得AC＝100米，则B点到河岸AD的距离为（）

A、100米 B、50 $\sqrt{3}$ 米 C、 $\frac{200 \sqrt{3}}{3}$ 米 D、50米

查看试题解析
6. 某店在开学初用880元购进若干个学生专用科学计算器，按每个50元出售，很快就销售一空，据了解学生还急需3倍这种计算器，于是又用2580元购进所需计算器，由于量大每个进价比上次优惠1元，该店仍按每个50元销售，最后剩下4个按九折卖出．这笔生意该店共盈利（）元．

A、508 B、520 C、528 D、560

查看试题解析
7. 在一个不透明的口袋中，装有若干个红球和6个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球试验发现，摸到黄球的频率是0.3，则估计盒子中大约有红球（）

A、16个 B、14个 C、20个 D、30个

查看试题解析
8. 若x>1，y>0，且满足xy=x^y ， $\frac{x}{y}$ =x³y，则x+y的值为（）

A、1 B、2 C、 $\frac{9}{2}$ D、 $\frac{11}{2}$

查看试题解析
9. 有两个一元二次方程M：ax²+bx+c=0；N：cx²+bx+a=0，其中ac≠0，a≠c.下列四个结论中：正确的个数有（）
①如果方程M有两个相等的实数根，那么方程N也有两个相等的实数根；②如果ac＜0，方程M、N都有两个不相等的实数根；③如果2是方程M的一个根，那么 $\frac{1}{2}$ 是方程N的一个根；④如果方程M和方程N有一个相同的根，那么这个根必是x=1.

A、4个 B、1个 C、2个 D、3个

查看试题解析
10. 如图所示的数码叫“莱布尼茨调和三角形”，它们是由整数的倒数组成的，第n行有n个数，且两端的数均为 $\frac{1}{n}$ ，每个数是它下一行左右相邻两数的和，则第8行第3个数（从左往右数）为（）

A、 $\frac{1}{60}$ B、 $\frac{1}{168}$ C、 $\frac{1}{280}$ D、 $\frac{1}{252}$

查看试题解析
11. 对于实数x，我们规定 $[x]$ 表示不大于x的最大整数，例如[1.2]=1，[3]=3，[-2.5]=-3，若 $[\frac{x + 4}{10}] = 5$ ，则x的取值可以是（）

A、40 B、45 C、51 D、56

查看试题解析
12. 如图，一个半径为r的圆形纸片在边长为a（ $a \geq 2 \sqrt{3} r$ ）的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“不能接触到的部分”的面积是（）

A、 $\sqrt{2}$ B、 $\frac{(3 \sqrt{3} - π)}{3} r^{2}$ C、 $(3 \sqrt{3} - π) r^{2}$ D、πr²

查看试题解析
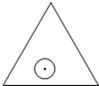13.
利用两块长方体测量一张桌子的高度，首先按图①方式放置，再交换木块的位置，按图②方式放置，测量的数据如图，则桌子的高度是（）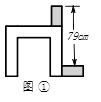

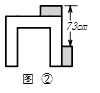A、 $73 c m$ B、 $74 c m$ C、 $75 c m$ D、 $76 c m$

查看试题解析
14. 如图，线段EF的长为4，O是EF的中点，以OF为边长做正方形OABC，连接AE、CF交于点P，将正方形OABC从OA与OF重合的位置开始，绕着点O逆时针旋转90°止，则点P运动的路径长为（）

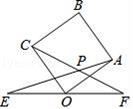A、 $\frac{\sqrt{2}}{2} π$ B、 $\sqrt{2} π$ C、2π D、 $2 \sqrt{2} π$

查看试题解析
15. 已知：二次函数y=ax²+bx+c（a≠0）的图象如图所示，下列结论中：①abc＞0；②2a+b＜0；③a+b＜m（am+b）（m≠1的实数）；④（a+c）²＜b²；⑤a＞1．其中正确的项是（）

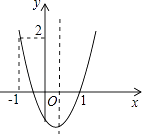A、①⑤ B、①②⑤ C、②⑤ D、①③④

查看试题解析

二、填空题

16. 如果单项式 $3 a^{4 x + 1} b^{2}$ 与 $- \frac{1}{2} a^{5} b^{3 y - 4}$ 可以合并为一.那么x与y的值应分别为.

查看试题解析
17. 夏洛特去山里寻宝，来到藏有宝藏的地方，发现这里有编号分为一，二，三，四，五的五扇大门，每扇门上都写有一句话：一，宝藏在五号大门的后面；二，宝藏或者在三号大门的后面，或者在五号的后面；三，宝藏不在五号大门的后面；四，宝藏不在此门后面；五，宝藏在二号大门的后面，夏洛特从当地人得到，五句话中只有一句是真的，那么夏洛特应该去号大门后面寻找宝藏．

查看试题解析
18. 已知a₁ ， a₂ ， a₃ ， …，a₂₀₁₉是彼此互不相等的负数，且M＝（a₁+a₂+a₃+…+a₂₀₁₈）（a₂+a₃+…+a₂₀₁₉），N＝（a₁+a₂+a₃+…+a₂₀₁₉）（a₂+a₃+…+a₂₀₁₈），那么M与N的大小关系是MN（填“＞”“＜”或“＝”）

查看试题解析
19. 为解决停车难得问题，在如图一段长56米的路段开辟停车位，每个车位是长5米、宽2.2米的矩形，矩形的边与路的边缘成45°角，那么这个路段最多可以划出个这样的停车位（ $\sqrt{2} \approx 1.4$ ）

查看试题解析
20. 电脑系统中有个“扫雷”游戏，要求游戏者标出所有的雷，游戏规则：一个方块下面最多埋一个雷，如果无雷，掀开方块下面就标有数字，提醒游戏者此数字周围的方块（最多八个）中雷的个数（实际游戏中，0通常省略不标，为方便大家识别与印刷，我把图乙中的0都标出来了，以示与未掀开者的区别），如图甲中的“3”表示它的周围八个方块中仅有3个埋有雷．图乙是张三玩游戏中的局部，图中有4个方块己确定是雷（方块上标有旗子），则图乙第一行从左数起的七个方块中（方块上标有字母），能够确定一定是雷的有．（请填入方块上的字母）

查看试题解析

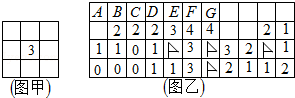
三、综合题

21. 阅读下面的材料，并解答下列问题：
已知： $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ，…

(1)、根据你发现的规律写出第n（n为正整数）个式子是；

(2)、计算： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{99 \times 100}$

(3)、用规律解方程： $\frac{1}{a (a + 1)} + \frac{1}{(a + 1) (a + 2)} + \dots + \frac{1}{(a + 2018) (a + 2019)} = \frac{1}{a + 2019}$ ．

查看试题解析
22. 计算：

(1)、 $\frac{a^{2} - 4}{a^{2} + 2 a + 1} \div \frac{a^{2} - 4 a + 4}{{(a + 1)}^{2}} - \frac{2}{a - 2}$ ；

(2)、先化简再求值：已知x= $\frac{1}{5} y$ ，求 $\frac{2 y}{x + 2 y} + \frac{x}{2 y - x} + \frac{4 x y}{4 y^{2} - x^{2}}$ ．

查看试题解析
23. 某校开展了“互助、平等、感恩、和谐、进取”主题班会活动，活动后，就活动的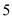个主题进行了抽样调查（每位同学只选最关注的一个），根据调查结果绘制了两幅不完整的统计图．根据图中提供的信息，解答下列问题：

(1)、这次调查的学生共有多少名；

(2)、请将条形统计图补充完整，并在扇形统计图中计算出“进取”所对应的圆心角的度数；

(3)、如果要在这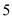个主题中任选两个进行调查，根据（2）中调查结果，用树状图或列表法，求恰好选到学生关注最多的两个主题的概率（将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E）．

查看试题解析
24. 如图，直径为10的⊙O经过原点O，并且与x轴、y轴分别交于A、B两点，线段OA、OB（OA＞OB）的长分别是方程x²+kx+48=0的两根．

(1)、求线段OA、OB的长；

(2)、已知点C在劣弧OA上，连结BC交OA于D，当OC²=CD·CB时，求C点的坐标；

(3)、在⊙O上是否存在点P，使S_△POD=S_△ABD ．若存在，求出点P的坐标；若不存在，请说明理由．

查看试题解析
25. 某工艺品厂生产一种汽车装饰品，每件生产成本为20元，销售价格在30元至80元之间（含30元和80元），销售过程中的管理、仓储、运输等各种费用（不含生产成本）总计50万元，其销售量y（万个）与销售价格（元/个）的函数关系如图所示.

(1)、当30≤x≤60时，求y与x的函数关系式；

(2)、求出该厂生产销售这种产品的纯利润w（万元）与销售价格x（元/个）的函数关系式；

(3)、销售价格应定为多少元时，获得利润最大，最大利润是多少？

查看试题解析
26. 如图，在平面直角坐标系中，抛物线y＝ax²+bx+4经过A（﹣3，0）、B（4，0）两点，且与y轴交于点C，D（4﹣4 $\sqrt{2}$ ，0）．动点P从点A出发，沿线段AB以每秒1个单位长度的速度向点B移动，同时动点Q从点C出发，沿线段CA以某一速度向点A移动．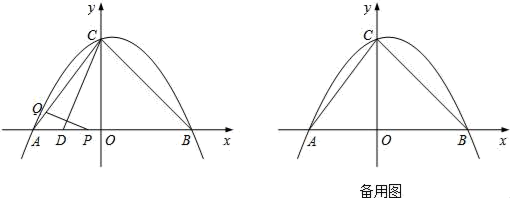

(1)、求该抛物线的解析式；

(2)、若经过t秒的移动，线段PQ被CD垂直平分，求此时t的值；

(3)、在第一象限的抛物线上取一点G，使得S_△GCB＝S_△GCA ，再在抛物线上找点E（不与点A、B、C重合），使得∠GBE＝45°，求E点的坐标．

查看试题解析
27. 已知：在矩形ABCD中，E为边BC上的一点，AE⊥DE，AB=12，BE=16，F为线段BE上一点，EF=7，连接AF．如图1，现有一张硬纸片△GMN，∠NGM=90⁰ ， NG=6，MG=8，斜边MN与边BC在同一直线上，点N与点E重合，点G在线段DE上．如图2，△GMN从图1的位置出发，以每秒1个单位的速度沿EB向点B匀速移动，同时，点P从A点出发，以每秒1个单位的速度沿AD向点D匀速移动，点Q为直线GN与线段AE的交点，连接PQ．当点N到达终点B时，△GMNP和点同时停止运动．设运动时间为t秒，解答问题：

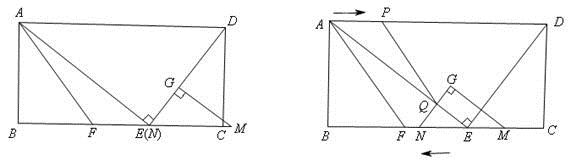(1)、在整个运动过程中，当点G在线段AE上时，求t的值；

(2)、在整个运动过程中，是否存在点P，使△APQ是等腰三角形，若存在，求出t的值；若不存在，说明理由；

(3)、在整个运动过程中，设△GMN与△AEF重叠部分的面积为S，请直接写出S与t的函数关系式以及自变量t的取值范围．

查看试题解析