四川省凉山州2020年中考数学模拟考试试卷

试卷更新日期：2020-05-06 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列方程是关于 $x$ 的一元二次方程的是（）

A、 $a x^{2} + b x + c = 0$ B、 $\frac{1}{x^{2}} + \frac{1}{x} = 2$ C、 $x^{2} + 2 x = x^{2} - 1$ D、 $3 {(x + 1)}^{2} = 2 (x + 1)$

查看试题解析
2.
如图，该图形围绕点O按下列角度旋转后，不能与其自身重合的是（）

A、72°　　 B、108° C、144°　　 D、216°

查看试题解析
3. 对于二次函数y＝2(x﹣3)²+2的图象，下列叙述正确的是（）

A、顶点坐标：(﹣3，2) B、对称轴是直线y＝3 C、当x＞3时，y随x增大而增大 D、当x＝0时，y＝2

查看试题解析
4. 如图，在半径为5cm的⊙O中，直线l交⊙O于A、B两点，且弦AB＝8cm ，要使直线l与⊙O相切，则需要将直线l向下平移（）

A、1cm B、2cm C、3cm D、4cm

查看试题解析
5. 直线y₁=x+1与抛物线y₂=﹣x²+3的图象如图，当y₁＞y₂时，x的取值范围为（）

A、x＜﹣2 B、x＞1 C、﹣2＜x＜1 D、x＜﹣2或x＞1

查看试题解析
6. 关于x的一元二次方程(a﹣1)x²+x+a²﹣1＝0的一个根为0，则a值为（）

A、1 B、﹣1 C、±1 D、0

查看试题解析
7. 如图，AB垂直于BC且AB＝BC＝3cm ， $\overset{⌢}{O A}$ 与 $\overset{⌢}{O C}$ 关于点O中心对称，AB、BC、 $\overset{⌢}{O A}$ 、 $\overset{⌢}{O C}$ 所围成的图形的面积是（）cm² ．

A、 $\frac{9}{2}$ B、 $\frac{9}{2}$ π C、 $\frac{3}{4}$ D、 $\frac{3}{4}$ π

查看试题解析
8. 下列说法中，正确的是（　　）

A、同一条弦所对的两条弧一定是等弧 B、长度相等的两条弧是等弧 C、正多边形一定是轴对称图形 D、三角形的外心到三角形各边的距离相等

查看试题解析
9. （m²-n²）（m²-n²-2）-8=0，则m²-n²的值是（）

A、4 B、-2 C、4或-2 D、-4或2

查看试题解析
10. 一个不透明口袋中装有3个红球2个白球，除颜色外都相同，从中任意摸出一个球，下列叙述正确的是（　　）

A、摸到红球是必然事件 B、摸到白球是不可能事件 C、摸到红球的可能性比白球大 D、摸到白球的可能性比红球大

查看试题解析
11. 如图，点A，B，C，D，E，F等分⊙O，分别以点B、D、F为圆心，AF的长为半径画弧，形成美丽的“三叶轮”图案．已知⊙O的半径为1，那么“三叶轮”图案的面积为（）

A、 $π$ + $\frac{3 \sqrt{3}}{2}$ B、 $π$ - $\frac{3 \sqrt{3}}{2}$ C、 $\frac{π + 3 \sqrt{3}}{2}$ D、 $\frac{π - 3 \sqrt{3}}{2}$

查看试题解析
12. 二次函数y＝ax²+bx+c的图象如图所示、则下列结论：①abc＞0；②a﹣5b+9c＞0；③3a+c＜0，正确的是（）

A、①③ B、①② C、①②③ D、②③

查看试题解析

二、填空题

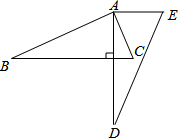
13. 若y＝(m²＋m)x^m2^－2m－1－x＋3是关于x的二次函数，则m＝．

查看试题解析
14. 如图，将△ABC绕点A逆时针旋转65°得△ADE ，若∠E＝70°，AD⊥BC ，则∠BAC＝．

查看试题解析
15. 若二次函数y＝ax²+bx+a²﹣2(a ， b为常数)的图象如图，则a＝．

查看试题解析
16. 一个均匀的立方体6个面上分别标有数1、2、3、4、5、6，下图是这个立方体表面展开图，抛掷这个立方体，则朝上一面上的数恰好等于下一面上的数的的概率是.

查看试题解析
17. 若二次函数 $y = a x^{2} + b x + c (a < 0)$ 的图像经过（2，0），且其对称轴为直线x=-1，则当函数值y>0成立时，x的取值范围是.

查看试题解析
18. 已知m、n是关于x的一元二次方程x²+px+q＝0的两个不相等的实数根，且m²+mn+n²＝3，则q的取值范围是．

查看试题解析
19. 如图．在Rt△ABC中，∠ACB＝90°，AC＝BC ，以A为圆心，AD长为半径的弧DF交AC的延长线于F ，若图中两个阴影部分的面积相等，则 $\frac{AD}{DB}$ ＝．

查看试题解析

三、计算题

20. 解方程

(1)、 $x^{2} - \sqrt{2} x - \frac{1}{4} = 0$

(2)、 $3 x (x - 1) = 2 (x - 1)$

查看试题解析
21. 已知关于x的一元二次方程x²-2kx+ $\frac{1}{2}$ k²-2=0.

(1)、求证:不论k为何值,方程总有两不相等实数根.

(2)、设x₁,x₂是方程的根,且 x₁²-2kx₁+2x₁x₂=5,求k的值.

查看试题解析

四、综合题

22. 小明对自己所在班级的50名学生平均每周参加课外活动的时间进行了调查，由调查结果绘制了频数分布直方图，
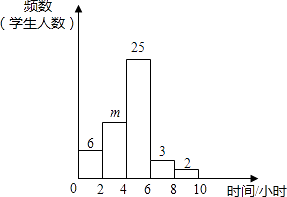
根据图中信息回答下列问题：

(1)、求m的值；

(2)、从参加课外活动时间在6～10小时的5名学生中随机选取2人，请你用列表或画树状图的方法，求其中至少有1人课外活动时间在8～10小时的概率．

查看试题解析
23. 如图，在平面直角坐标系中，点P(3，4)，连接OP ，将线段OP绕点O逆时针旋转90°得线段OP₁ ．

(1)、在图中作出线段OP₁ ，并写出P₁点的坐标；

(2)、求点P在旋转过程中所绕过的路径长；

(3)、求线段OP在旋转过程中所扫过的图形的面积．

查看试题解析
24. 如图，已知在⊙O中，直径MN＝10，正方形ABCD的四个顶点分别在⊙O及半径OM、OP上，并且∠POM＝45°，求正方形的边长．

查看试题解析
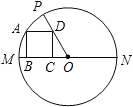25. 一个容器盛满纯酒20升，第一次倒出纯酒精若干升后，加水注满，第二次倒出相同数量的酒精，这时容器内的纯酒精只是原来的 $\frac{1}{4}$ ，问第一次倒出纯酒精多少升？

查看试题解析
26. 某校九年级决定购买学习用具对在本次适应性考以中成绩突出的同学进行奖励，其中计划购买，A、B两种型号的钢笔共45支，已知A种钢笔的单价为7元/支，购买B种钢笔所需费用y(元)与购买数量x(支)之间存在如图所示的函数关系式．

(1)、求y与x的函数关系式；

(2)、若购买计划中，B种钢笔的数最不超过35支，但不少于A种钢笔的数量，请设计购买方案，使总费用最低，并求出最低费用．

查看试题解析
27. 如图⊙O的直径AB＝10cm ，弦BC＝6cm ， ∠ACB的平分线交⊙O于D ，交AB于E ， P是AB延长线上一点，且PC＝PE ．

(1)、求证：PC是⊙O的切线；

(2)、求AC、AD的长．

查看试题解析
28. 如图，抛物线y＝﹣x²+bx+c经过A(﹣1，0)，C(0，3)两点，点B是抛物线与x轴的另一个交点，点D与点C关于抛物线对称轴对称，作直线AD ．点P在抛物线上，过点P作PE⊥x轴，垂足为点E ，交直线AD于点Q ，过点P作PG⊥AD ，垂足为点G ，连接AP ．设点P的横坐标为m ， PQ的长度为d ．

(1)、求抛物线的解析式；

(2)、求点D的坐标及直线AD的解析式；

(3)、当点P在直线AD上方时，求d关于m的函数关系式，并求出d的最大值；

(4)、当点P在直线AD上方时，若PQ将△APG分成面积相等的两部分，直接写出m的值．

查看试题解析