四川省成都市成华区2020年中考数学一模考试试卷

试卷更新日期：2020-05-06 类型：中考模拟

进入出卷网下载

一、选择题

1. 2cos60°=（）

A、1 B、 $\sqrt{3}$ C、 $\sqrt{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 下面四个英文字母图案，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图所示物体的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 矩形具有而平行四边形不一定具有的性质是（）

A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分

查看试题解析
5. 反比例函数 $y = - \frac{3}{x}$ ，下列说法不正确的是（）

A、图象经过点(1，－3) B、图象位于第二、四象限 C、图象关于直线y=x对称 D、y随x的增大而增大

查看试题解析
6. 若一元二次方程x²﹣2x+m=0有两个不相同的实数根，则实数m的取值范围是（）

A、m≥1 B、m≤1 C、m＞1 D、m＜1

查看试题解析
7. 一个等腰三角形的两条边长分别是方程 $x^{2} - 7 x + 10 = 0$ 的两根，则该等腰三角形的周长是（）

A、12 B、9 C、13 D、12或9

查看试题解析
8. 如图，△ABC中，AB＝AC，BC＝10，∠B＝36°，D为BC的中点，则AD的长是（）

A、5sin36° B、5cos36° C、5tan36° D、10tan36°

查看试题解析
9. 在如图所示的象棋盘（各个小正方形的边长均相等）中，根据“马走日”的规则，“马”应落在下列哪个位置处，能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”，“兵”所在位置的格点构成的三角形相似（）

A、①处 B、②处 C、③处 D、④处

查看试题解析
10. 已知抛物线y=ax²+bx+c（a≠0）的对称轴为直线x=2，与x轴的一个交点坐标为（4，0），其部分图象如图所示，下列结论：
①抛物线过原点；
②4a+b+c=0；
③a﹣b+c＜0；
④抛物线的顶点坐标为（2，b）；
⑤当x＜2时，y随x增大而增大．
其中结论正确的是（）

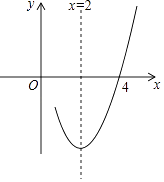A、①②③ B、③④⑤ C、①②④ D、①④⑤

查看试题解析

二、填空题

11. 一元二次方程 $x (x - 2) = x - 2$ 的根是.

查看试题解析
12. 如果反比例函数 $y = \frac{a - 2}{x}$ （ $a$ 是常数）的图象在第一、三象限，那么 $a$ 的取值范围是.

查看试题解析
13. 受非洲猪瘟及供求关系影响，去年猪肉价格经过连续两轮涨价，价格从40元/千克涨到90元/千克，若两轮涨价的百分率相同，则这个百分率是．

查看试题解析
14. 如图，周长为16的菱形ABCD的对角线AC，BD相交于点O，∠BAD＝60°，分别以点C，D为圆心，大于 $\frac{1}{2}$ CD为半径画弧，两弧交于点M、N，直线MN交CD于点E，则△OCE的面积．

查看试题解析

三、计算题

15.

(1)、计算； ${(- 1)}^{2020} + {(π - 3.14)}^{0} + 2 \sin 45^{°} - \sqrt{16}$

(2)、解方程：（x+8）（x+1）＝﹣12．

查看试题解析
16. 先化简，再求代数式（1﹣ $\frac{1}{a - 2}$ ）÷ $\frac{a^{2} - 6 a + 9}{2 a - 4}$ 的值，其中a=4cos30°+3tan45°.

查看试题解析

四、综合题

17. 某校调查了若干名家长对“初中生带手机上学”现象的看法，统计整理并制作了如下的条形与扇形统计图，根据图中提供的信息，完成以下问题：

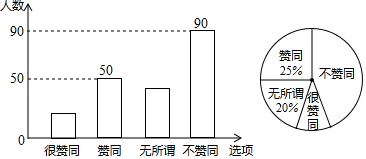(1)、本次共调查了名家长；扇形统计图中“很赞同”所对应的圆心角是度．已知该校共有1600名家长，则“不赞同”的家长约有名；请补全条形统计图；

(2)、从“不赞同”的五位家长中（两女三男），随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座，请用树状图或列表法求出选中“1男1女”的概率．

查看试题解析
18. 小明想测量湿地公园内某池塘两端A，B两点间的距离．他沿着与直线AB平行的道路EF行走，当行走到点C处，测得∠ACF＝40°，再向前行走100米到点D处，测得∠BDF＝52.44°，若直线AB与EF之间的距离为60米，求A，B两点的距离（结果精确到0.1）（参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，sin52.44°≈0.79，cos52.44°≈0.61，tan52.44°≈1.30）

查看试题解析
19. 如图，一次函数y＝﹣x+3的图象与反比例函数y＝ $\frac{k}{x}$ （k≠0）在第一象限的图象交于A(1，a)和B两点，与x轴交于点C．

(1)、求反比例函数的解析式及点A的坐标；

(2)、若点P为x轴上一点，且满足△ACP是等腰三角形，请直接写出符合条件的所有点P的坐标．

查看试题解析
20. 在△ABC中，BC＝6，S_△ABC＝18，正方形DEFG的边FG在BC上，顶点D，E分别在AB，AC上．

(1)、如图1，过点A作AH⊥BC于点H，交DE于点K，求正方形DEFG的边长；

(2)、如图2，在BE上取点M，作MN⊥BC于点N，MQ∥DE交AB于点Q，QP⊥BC于点P，求证：四边形MNPQ是正方形；

(3)、如图3，在BE上取点R，使RE＝FE，连结RG，RF，若tan∠EBF＝ $\frac{3}{4}$ ．求证：∠GRF＝90°．

查看试题解析
21. 若方程x²﹣2x﹣4＝0的两个实数根为α，β，则α²+β²的值为．

查看试题解析
22. 第一象限的点A(a，b)和它关于x轴的对称点B分别在双曲线y＝ $\frac{k_{1}}{x}$ 和y＝ $\frac{k_{2}}{x}$ 上，则k₁+k₂的值为．

查看试题解析
23. 如图电路中，随机闭合开关S₁ ， S₂ ， S₃ ， S₄中的两个，能够点亮灯泡的概率为．

查看试题解析
24. 如图，把矩形ABCD沿EF，GH折叠，使点B，C落在AD上同一点P处，∠FPG＝90°，△A′EP的面积是8 $\sqrt{2}$ ，△D′PH的面积是4 $\sqrt{2}$ ，则矩形ABCD的面积等于．

查看试题解析
25. 规定：如果一个四边形有一组对边平行，一组邻边相等，那么称此四边形为广义菱形．根据规定判断下面四个结论：①正方形和菱形都是广义菱形；②平行四边形是广义菱形；③对角线互相垂直，且两组邻边分别相等的四边形是广义菱形；④若M、N的坐标分别为 $(0, 1), (0, - 1),$ P是二次函数 $y = \frac{1}{4} x^{2}$ 的图象上在第一象限内的任意一点，PQ垂直直线 $y = - 1$ 于点Q ，则四边形PMNQ是广义菱形．其中正确的是．（填序号）

查看试题解析
26. 某宾馆有若干间标准房，当标准房的价格为200元时，每天入住的房间数为60间，经市场调查表明，该宾馆每间标准房的价格在170~240元之间（含170元，240元）浮动时，每天入住的房间数y（间）与每间标准房的价格x（元）的数据如下表：

x（元）

…

190

200

210

220

…

y(间)

…

65

60

55

50

…

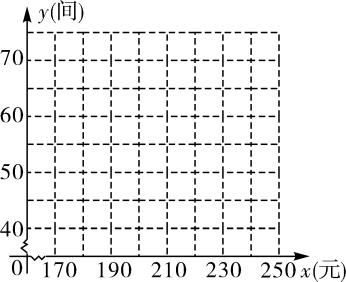(1)、根据所给数据在坐标系中描出相应的点，并画出图象。

(2)、求y关于x的函数表达式、并写出自变量x的取值范围.

(3)、设客房的日营业额为w（元）。若不考虑其他因素，问宾馆标准房的价格定为多少元时。客房的日营业额最大?最大为多少元？

查看试题解析
27. 如图，在正方形ABCD中，AB＝6，点E在对角线BD上，DE＝2 $\sqrt{2}$ ，连接CE，过点E作EF⊥CE，交线段AB于点F

(1)、求证：CE＝EF；

(2)、求FB的长；

(3)、连接FC交BD于点G．求BG的长．

查看试题解析
28. 已知抛物线y＝ax²+bx+3与x轴分别交于点A(﹣3，0)，B(1，0)交于点C，抛物线的顶点为点D．

(1)、抛物线的表达式及顶点D的坐标．

(2)、若点F是线段AD上一个动点，
①如图1，当FC+FO的值最小时，求点F的坐标；

②如图2，以点A，F，O为顶点的三角形能否与△ABC相似？若能，求出点F的坐标；若不能，请说明理由．

查看试题解析

x（元）	…	190	200	210	220	…
y(间)	…	65	60	55	50	…