四川省巴中市平昌县2020年中考数学网络模拟考试试卷
试卷更新日期:2020-05-06 类型:中考模拟
一、选择题
-
1. 3倒数等于( )A、3 B、 C、﹣3 D、﹣2. 下列运算:①a2•a3=a6 , ②(a3)2=a6 , ③a5÷a5=a,④(ab)3=a3b3 , 其中结果正确的个数为( )A、1 B、2 C、3 D、43. 如图,该几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 不透明的袋子中装有红球1个、绿球1个、白球2个,除颜色外无其他差别.随机摸出一个小球后不放回,再摸出一个球,则两次都摸到白球的概率是( )A、 B、 C、 D、5. 不等式组 的解在数轴上表示为( )A、
4. 不透明的袋子中装有红球1个、绿球1个、白球2个,除颜色外无其他差别.随机摸出一个小球后不放回,再摸出一个球,则两次都摸到白球的概率是( )A、 B、 C、 D、5. 不等式组 的解在数轴上表示为( )A、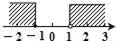 B、
B、 C、
C、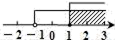 D、
D、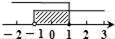 6. 如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( )
6. 如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( ) A、∠AIB=∠AOB B、∠AIB≠∠AOB C、4∠AIB﹣∠AOB=360° D、2∠AOB﹣∠AIB=180°7. 如图,正方形ABCD内接于⊙O,AB=2 ,则 的长是( )
A、∠AIB=∠AOB B、∠AIB≠∠AOB C、4∠AIB﹣∠AOB=360° D、2∠AOB﹣∠AIB=180°7. 如图,正方形ABCD内接于⊙O,AB=2 ,则 的长是( )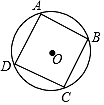 A、π B、 π C、2π D、 π8. 如图,在6×4的正方形网格中,△ABC的顶点均为格点,则sin∠ACB=( )
A、π B、 π C、2π D、 π8. 如图,在6×4的正方形网格中,△ABC的顶点均为格点,则sin∠ACB=( )
A、 B、2 C、 D、9. 如图,点A为反比例函数y=﹣ 图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为( ) A、4 B、﹣2 C、2 D、无法确定10. 如图,是二次函数 图象的一部分,其对称轴是 ,且过点 ,下列说法: ; ; ; 若 , 是抛物线上两点,则 ,其中正确的有
A、4 B、﹣2 C、2 D、无法确定10. 如图,是二次函数 图象的一部分,其对称轴是 ,且过点 ,下列说法: ; ; ; 若 , 是抛物线上两点,则 ,其中正确的有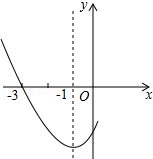 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如果 是完全平方式,则 .12. 一个角的补角为130°,那么这个角的余角度数是。13. 如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形B、C、D的面积依次为4、3、9,则正方形A的面积为 .
 14. 若 ,则(b﹣a)2015= .15. 如图,△ABC中,∠BAC=90°,AB=AC,顶点A在x轴负半轴上,B在y轴正半轴上,且C(4,﹣4),则点B的坐标为 .
14. 若 ,则(b﹣a)2015= .15. 如图,△ABC中,∠BAC=90°,AB=AC,顶点A在x轴负半轴上,B在y轴正半轴上,且C(4,﹣4),则点B的坐标为 . 16. 如图,AB是⊙O的直径,CD是⊙O的弦,∠DCB=32°.则∠ABD=
16. 如图,AB是⊙O的直径,CD是⊙O的弦,∠DCB=32°.则∠ABD= 17. 如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,则△ODE与△AOB的面积比为 .
17. 如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,则△ODE与△AOB的面积比为 . 18. 半径为2的圆被四等分切割成四条相等的弧,将四个弧首尾顺次相连拼成如图所示的恒星图型,那么这个恒星的面积等于.
18. 半径为2的圆被四等分切割成四条相等的弧,将四个弧首尾顺次相连拼成如图所示的恒星图型,那么这个恒星的面积等于. 19. 在实数范围内分解因式:x2y﹣3y= .20. 如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE , 连接CE、BD交于点G , 连接AG , 那么∠AGD的底数是度.
19. 在实数范围内分解因式:x2y﹣3y= .20. 如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE , 连接CE、BD交于点G , 连接AG , 那么∠AGD的底数是度.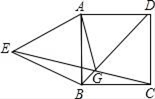
三、综合题
-
21. 计算:( )﹣2+(π﹣3)0﹣ +tan45°.22. 已知关于x的一元二次方程x2﹣mx﹣3=0…①.(1)、对于任意的实数m , 判断方程①的根的情况,并说明理由.(2)、若x=﹣1是这个方程的一个根,求m的值和方程①的另一根.23. 先化简,再求值:(1﹣ )÷ ,其中x= +2.24. 在▱ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H,求证:CH=EH.
 25. 某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
25. 某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图. (1)、这次被调查的同学共有人;(2)、补全条形统计图,并在图上标明相应的数据;(3)、校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐.26. 如图,在平面直角坐标系中,△AOB的三个顶点坐标分别为A(1,0),O(0,0),B(2,2).以点O为旋转中心,将△AOB逆时针旋转90°,得到△A1OB1 .
(1)、这次被调查的同学共有人;(2)、补全条形统计图,并在图上标明相应的数据;(3)、校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐.26. 如图,在平面直角坐标系中,△AOB的三个顶点坐标分别为A(1,0),O(0,0),B(2,2).以点O为旋转中心,将△AOB逆时针旋转90°,得到△A1OB1 . (1)、画出△A1OB1;(2)、直接写出点A1和点B1的坐标;(3)、求线段OB1的长度.27. 甲商品的进价为每件20元,商场将其售价从原来的每件40元进行两次调价,已知该商品现价为每件32.4元.(1)、若该商品两次调价的降价率相同,求这个降价率;(2)、经调查,该商品每降价0.2元,即可多销售10件. 已知甲商品售价40元时每月可销售500件,若该商场希望该商品每月能盈利10000元,且尽可能扩大销售量,则该商品在现价的基础上还应如何调整?28. 如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
(1)、画出△A1OB1;(2)、直接写出点A1和点B1的坐标;(3)、求线段OB1的长度.27. 甲商品的进价为每件20元,商场将其售价从原来的每件40元进行两次调价,已知该商品现价为每件32.4元.(1)、若该商品两次调价的降价率相同,求这个降价率;(2)、经调查,该商品每降价0.2元,即可多销售10件. 已知甲商品售价40元时每月可销售500件,若该商场希望该商品每月能盈利10000元,且尽可能扩大销售量,则该商品在现价的基础上还应如何调整?28. 如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D. (1)、求证:AC平分∠DAB;(2)、若CD=4,AD=8,试求⊙O的半径.29. 如图,点A(m,m+1),B(m+3,m﹣1)是反比例函数 (x>0)与一次函数y=ax+b的交点.
(1)、求证:AC平分∠DAB;(2)、若CD=4,AD=8,试求⊙O的半径.29. 如图,点A(m,m+1),B(m+3,m﹣1)是反比例函数 (x>0)与一次函数y=ax+b的交点.
求:
(1)、反比例函数与一次函数的解析式;(2)、根据图象直接写出当反比例函数的函数值大于一次函数的函数值时x的取值范围.30. 在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m , 拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2). (1)、如图1,若BC=4m , 则S=m2 .(2)、如图2,现考虑在(1)中矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其他条件不变,则在BC的变化过程中,当S取得最小值时,边BC的长为m .31. 如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y= x2﹣x交于A、B两点.
(1)、如图1,若BC=4m , 则S=m2 .(2)、如图2,现考虑在(1)中矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其他条件不变,则在BC的变化过程中,当S取得最小值时,边BC的长为m .31. 如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y= x2﹣x交于A、B两点.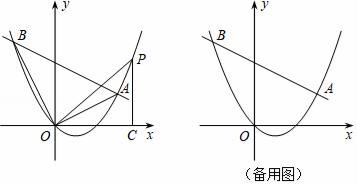 (1)、直线总经过定点,请直接写出该定点的坐标;(2)、点P在抛物线上,当k=﹣ 时,解决下列问题:
(1)、直线总经过定点,请直接写出该定点的坐标;(2)、点P在抛物线上,当k=﹣ 时,解决下列问题:①在直线AB下方的抛物线上求点P,使得△PAB的面积等于20;
②连接OA,OB,OP,作PC⊥x轴于点C,若△POC和△ABO相似,请直接写出点P的坐标.