四川省绵阳市安县2019年中考数学二模考试试卷
试卷更新日期:2020-05-06 类型:中考模拟
一、选择题
-
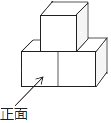
1. 的倒数是( )A、 B、 C、 D、2. 如图是由三个相同的小正方体组成的几何体,则该几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 我国倡导的“一带一路”将促进中国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总人口为 人,这个数用科学记数法表示为( )A、 B、 C、 D、4. 已知已知 、 是一元二次方程 的两根,则 的值是( )A、 B、 C、 D、5. 在平面直角坐标系中,以原点为中心,把点 逆时针旋转 ,得到点 ,则点 的坐标为( )A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 在一次数学答题比赛中,五位同学答对题目的个数分别为7,5,3,5,10,则关于这组数据的说法不正确的是( )
3. 我国倡导的“一带一路”将促进中国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总人口为 人,这个数用科学记数法表示为( )A、 B、 C、 D、4. 已知已知 、 是一元二次方程 的两根,则 的值是( )A、 B、 C、 D、5. 在平面直角坐标系中,以原点为中心,把点 逆时针旋转 ,得到点 ,则点 的坐标为( )A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 在一次数学答题比赛中,五位同学答对题目的个数分别为7,5,3,5,10,则关于这组数据的说法不正确的是( )
A、众数是5 B、中位数是5 C、平均数是6 D、方差是3.68. 如图,已知AB是⊙O的直径,BC是弦,∠ABC=30°,过圆心O作OD⊥BC,垂足为E,交弧BC于点D,连接DC,则∠DCB的度数为( ) A、30° B、45° C、50° D、60°9. 将抛物线y=﹣5x2+1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( )A、y=﹣5(x+1)2﹣1 B、y=﹣5(x﹣1)2﹣1 C、y=﹣5(x+1)2+3 D、y=﹣5(x﹣1)2+310. 如图,在平行四边形 中, 平分 ,交 于点 , 平分 ,交 于点 , , ,则 长为( )
A、30° B、45° C、50° D、60°9. 将抛物线y=﹣5x2+1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( )A、y=﹣5(x+1)2﹣1 B、y=﹣5(x﹣1)2﹣1 C、y=﹣5(x+1)2+3 D、y=﹣5(x﹣1)2+310. 如图,在平行四边形 中, 平分 ,交 于点 , 平分 ,交 于点 , , ,则 长为( ) A、8 B、9 C、10 D、1211. 如图,二次函数 的图象过点 ,对称轴为直线 ,给出以下结论:① ;② ;③ :④若 为函数图象上的两点,则 .其中正确的是( )
A、8 B、9 C、10 D、1211. 如图,二次函数 的图象过点 ,对称轴为直线 ,给出以下结论:① ;② ;③ :④若 为函数图象上的两点,则 .其中正确的是( ) A、①②④ B、①②③ C、①③④ D、①②③④12. 如图,AB为半圆O的直径,C是半圆上一点,且∠COA=60°,设扇形AOC,△COB,弓形BmC的面积为S1、S2、S3 , 则它们之间的关系是( )
A、①②④ B、①②③ C、①③④ D、①②③④12. 如图,AB为半圆O的直径,C是半圆上一点,且∠COA=60°,设扇形AOC,△COB,弓形BmC的面积为S1、S2、S3 , 则它们之间的关系是( )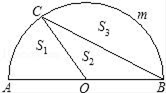 A、S1<S2<S3 B、S2<S1<S3 C、S1<S3<S2 D、S3<S2<S1
A、S1<S2<S3 B、S2<S1<S3 C、S1<S3<S2 D、S3<S2<S1二、填空题
-
13. 分解因式: .14. 已知袋中有若干个小球,它们除颜色外其它都相同,其中只有2个红球,若随机从中摸出一个,摸到红球的概率是 ,则袋中小球的总个数是15. 已知a、b满足(a﹣1)2+ =0,则a+b= .16. 用一段长为30m的篱笆围成一个一边靠墙的矩形菜园,墙长20m,当矩形的长、宽各取某个特定的值时,菜园的面积最大,这个最大面积是m2.
 17. 如图,小玲家在某24层楼的顶楼,对面新建了一幢28米高的图书馆,小玲在楼顶 处看图书馆楼顶 处和楼底 处的俯角分别是 ∘,则两楼之间的距离是米.
17. 如图,小玲家在某24层楼的顶楼,对面新建了一幢28米高的图书馆,小玲在楼顶 处看图书馆楼顶 处和楼底 处的俯角分别是 ∘,则两楼之间的距离是米. 18. 如图,把 绕点 逆时针旋转 ,得到 点 恰好落在边 上,连接 ,则 .
18. 如图,把 绕点 逆时针旋转 ,得到 点 恰好落在边 上,连接 ,则 .
三、综合题
-
19.(1)、计算(2)、先化简,再求值: ,其中 满足20. 据新浪网调查,在第十二届全国人大二中全会后,全国网民对政府工作报告关注度非常高,大家关注的网民们关注的热点话题分别有:消费、教育、环保、反腐、及其它共五类,且关注五类热点问题的网民的人数所占百分比如图l所示,关注该五类热点问题网民的人数的不完整条形统计如图2所示,请根据图中信息解答下列问题.
 (1)、求出图l中关注“反腐”类问题的网民所占百分比x的值,并将图2中的不完整的条形统计图补充完整;(2)、为了深入探讨政府工作报告,新浪网邀请成都市5名网民代表甲、乙、丙、丁、戊做客新浪访谈,且一次访谈只选2名代表,请你用列表法或画树状图的方法,求出一次所选代表恰好是甲和乙的概率.21. 某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.(1)、求每件甲种、乙种玩具的进价分别是多少元?(2)、商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?22. 如图,在平面直角坐标系 中,一次函数 的图象经过点 ,与反比例函数 的图象交于 .
(1)、求出图l中关注“反腐”类问题的网民所占百分比x的值,并将图2中的不完整的条形统计图补充完整;(2)、为了深入探讨政府工作报告,新浪网邀请成都市5名网民代表甲、乙、丙、丁、戊做客新浪访谈,且一次访谈只选2名代表,请你用列表法或画树状图的方法,求出一次所选代表恰好是甲和乙的概率.21. 某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.(1)、求每件甲种、乙种玩具的进价分别是多少元?(2)、商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?22. 如图,在平面直角坐标系 中,一次函数 的图象经过点 ,与反比例函数 的图象交于 .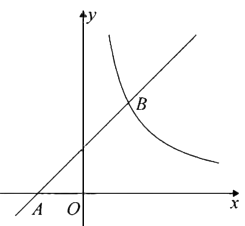 (1)、求一次函数和反比例函数的表达式;(2)、设 是直线 上一点,过 作 轴,交反比例函数 的图象于点 ,若 为顶点的四边形为平行四边形,求点 的坐标.
(1)、求一次函数和反比例函数的表达式;(2)、设 是直线 上一点,过 作 轴,交反比例函数 的图象于点 ,若 为顶点的四边形为平行四边形,求点 的坐标.
23. 如图, 中, ,以 为直径的 交 边于点 ,连接 ,过 作 的垂线,交 边于点 ,交 边的延长线于点 . (1)、求证: 是 的切线;(2)、若 , ,求劣弧 的长.24. 如图,已知一个三角形纸片 ,其中 , 分别是 边上的点,连接 .
(1)、求证: 是 的切线;(2)、若 , ,求劣弧 的长.24. 如图,已知一个三角形纸片 ,其中 , 分别是 边上的点,连接 .
 (1)、如图,若将纸片 的一角沿 折叠,折叠后点 落在 边上的点 处,且使S四边形ECBF ,求 的长;(2)、如图,若将纸片 的一角沿 折叠,折叠后点 落在 边上的点 处,且使 .试判断四边形 的形状,并证明你的结论.25. 如图1,抛物线的顶点A的坐标为(1,4),抛物线与x轴相交于B、C两点,与y轴交于点E(0,3).
(1)、如图,若将纸片 的一角沿 折叠,折叠后点 落在 边上的点 处,且使S四边形ECBF ,求 的长;(2)、如图,若将纸片 的一角沿 折叠,折叠后点 落在 边上的点 处,且使 .试判断四边形 的形状,并证明你的结论.25. 如图1,抛物线的顶点A的坐标为(1,4),抛物线与x轴相交于B、C两点,与y轴交于点E(0,3).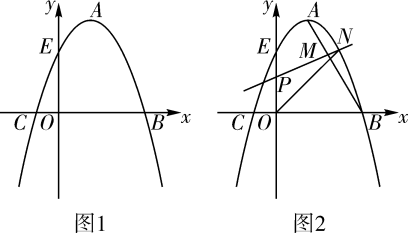 (1)、求抛物线的表达式;(2)、已知点F(0,﹣3),在抛物线的对称轴上是否存在一点G,使得EG+FG最小,如果存在,求出点G的坐标;如果不存在,请说明理由.(3)、如图2,连接AB,若点P是线段OE上的一动点,过点P作线段AB的垂线,分别与线段AB、抛物线相交于点M、N(点M、N都在抛物线对称轴的右侧),当MN最大时,求△PON的面积.
(1)、求抛物线的表达式;(2)、已知点F(0,﹣3),在抛物线的对称轴上是否存在一点G,使得EG+FG最小,如果存在,求出点G的坐标;如果不存在,请说明理由.(3)、如图2,连接AB,若点P是线段OE上的一动点,过点P作线段AB的垂线,分别与线段AB、抛物线相交于点M、N(点M、N都在抛物线对称轴的右侧),当MN最大时,求△PON的面积.