四川省达州市开江县2019年中考数学二模考试试卷
试卷更新日期:2020-05-06 类型:中考模拟
一、选择题
-
1. 的倒数是( )A、 B、2019 C、 D、2. 如图所示的几何体是由6个大小相同的小立方块搭成,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 根据财政部近期披露的2019年中央财政预算报告相关数据知:今年全国预计减税降费近2万亿元,进一步实现所有行业税负只减不增的目标.数据2万亿用科学记数法表示应为( )A、 B、 C、 D、4. 不等式组 的解集在数轴上表示正确的是( )A、
3. 根据财政部近期披露的2019年中央财政预算报告相关数据知:今年全国预计减税降费近2万亿元,进一步实现所有行业税负只减不增的目标.数据2万亿用科学记数法表示应为( )A、 B、 C、 D、4. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图是成都市某周内日最高气温的折线统计图,关于这7天的日最高气温的说法正确的是( )
5. 如图是成都市某周内日最高气温的折线统计图,关于这7天的日最高气温的说法正确的是( )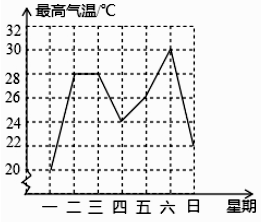 A、极差是8℃ B、众数是28℃ C、中位数是24℃ D、平均数是26℃6. 下列说法中正确的是( )A、同一平面内,过一点有且只有一条直线与已知直线平行 B、三张分别画有菱形、等边三角形、圆的卡片,从中随机抽取一张,恰好抽到中心对称图形卡片的概率是 C、一组对边平行,一组对边相等的四边形是平行四边形 D、当 时,关于 的方程 有实数根7. 如图,将含30°角的直角三角板ABC的直角顶点C放在直尺的一边上,已知∠A=30°,∠1=40°,则∠2的度数为( )
A、极差是8℃ B、众数是28℃ C、中位数是24℃ D、平均数是26℃6. 下列说法中正确的是( )A、同一平面内,过一点有且只有一条直线与已知直线平行 B、三张分别画有菱形、等边三角形、圆的卡片,从中随机抽取一张,恰好抽到中心对称图形卡片的概率是 C、一组对边平行,一组对边相等的四边形是平行四边形 D、当 时,关于 的方程 有实数根7. 如图,将含30°角的直角三角板ABC的直角顶点C放在直尺的一边上,已知∠A=30°,∠1=40°,则∠2的度数为( )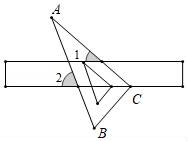 A、55° B、60° C、65° D、70°8. 如图,在边长为6的菱形 中, ,以点 为圆心,菱形的高 为半径画弧,交 于点 ,交 于点 ,则图中阴影部分的面积是( )
A、55° B、60° C、65° D、70°8. 如图,在边长为6的菱形 中, ,以点 为圆心,菱形的高 为半径画弧,交 于点 ,交 于点 ,则图中阴影部分的面积是( )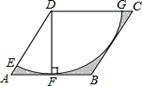 A、 B、 C、 D、9. 如图所示,矩形 中, 是 的中点,将 沿 翻折,点 落在点 处, ,设 , 的面积为 ,则 与 的函数图象大致为( )
A、 B、 C、 D、9. 如图所示,矩形 中, 是 的中点,将 沿 翻折,点 落在点 处, ,设 , 的面积为 ,则 与 的函数图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,在正方形 中, 是对角线 与 的交点, 是 边上的动点(点 不与 重合),过点 作 垂直 交 于点 ,连结 .下列四个结论:① ;② ;③ ;④若 ,则 的最小值是1.其中正确结论是( )
10. 如图,在正方形 中, 是对角线 与 的交点, 是 边上的动点(点 不与 重合),过点 作 垂直 交 于点 ,连结 .下列四个结论:① ;② ;③ ;④若 ,则 的最小值是1.其中正确结论是( ) A、①②③ B、①③④ C、①②④ D、②③④
A、①②③ B、①③④ C、①②④ D、②③④二、填空题
-
11. 分解因式:3a3﹣12a2+12a= .12. 两市相距150千米,甲车从 市到 市,乙车从 市到 市,两车同时出发,已知甲车速度比乙车快20千米/小时,甲车比乙车早半小时到达目的地.若设乙车的速度是 千米/小时,则根据题意,可列方程 .13. 有9张卡片,分别写有 这九个数字,将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,则关于x的不等式组 有解的概率为.14. 已知关于的 方程 有两个实数根,则 的取值范围是 .15. 如图,在 中, ,点 为 上任意一点,连接 ,以 为邻边作平行四边形 ,连接 ,则 的最小值为.
 16. 如图,在平面直角坐标系中,正方形 的顶点 的坐标为 ,点 在 轴正半轴上,点 在第三象限的双曲线 上,过点 作 轴交双曲线于点 ,连接 ,则 的面积为.
16. 如图,在平面直角坐标系中,正方形 的顶点 的坐标为 ,点 在 轴正半轴上,点 在第三象限的双曲线 上,过点 作 轴交双曲线于点 ,连接 ,则 的面积为.
三、计算题
-
17. 计算: ;18. 先化简,再求值: ,其中 的值满足方程: .
四、综合题
-
19. 在达州市关工委组织的“五好小公民”主题教育活动中,我市某中学组织全校学生参加了“红旗队飘,引我成长”知识竞赛,赛后机抽取了部分参赛学生的成绩,从高分到低分将成绩分成 五类,绘制成下面两个不完整的统计图:


根据上面提供的信息解答下列问题:
(1)、补全条形统计图;(2)、若该校共有学生4200人,求成绩为 类的学生人数和 类学生所对应的圆心角的度数;(3)、若 类恰好是2名男生和2名女生,随机选择2名学生担任校园广播“孝心伴我行”节目主持人,请用列表法或画树状图法求恰好抽到1名男生和1名女生的概率.20. 如图,男生楼在女生楼的左侧,两楼高度均为90m,楼间距为AB,冬至日正午,太阳光线与水平面所成的角为 ,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为 ,女生楼在男生楼墙面上的影高为DA,已知 .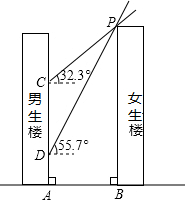 (1)、求楼间距AB;(2)、若男生楼共30层,层高均为3m,请通过计算说明多少层以下会受到挡光的影响? 参考数据: , , , , ,21. 如图,在平面直角坐标系 中,一次函数 的图象经过点 ,与反比例函数 的图象交于 .
(1)、求楼间距AB;(2)、若男生楼共30层,层高均为3m,请通过计算说明多少层以下会受到挡光的影响? 参考数据: , , , , ,21. 如图,在平面直角坐标系 中,一次函数 的图象经过点 ,与反比例函数 的图象交于 .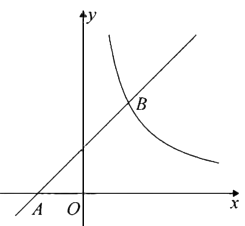 (1)、求一次函数和反比例函数的表达式;(2)、设 是直线 上一点,过 作 轴,交反比例函数 的图象于点 ,若 为顶点的四边形为平行四边形,求点 的坐标.
(1)、求一次函数和反比例函数的表达式;(2)、设 是直线 上一点,过 作 轴,交反比例函数 的图象于点 ,若 为顶点的四边形为平行四边形,求点 的坐标.
22. 如图,在 中, ,以 为直径作圆 ,分别交 于点 ,交 的延长线于点 ,过点 作 于点 ,连接 交线段 于点 . (1)、求证: 是圆 的切线;(2)、若 为 的中点,求 的值;(3)、若 ,求圆 的半径.23. 为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有A,B两种型号的健身器材可供选择.(1)、劲松公司2015年每套A型健身器材的售价为2.5万元,经过连续两年降价,2017年每套售价为1.6万元,求每套A型健身器材年平均下降率n;(2)、2017年市政府经过招标,决定年内采购并安装劲松公司A,B两种型号的健身器材共80套,采购专项经费总计不超过112万元,采购合同规定:每套A型健身器材售价为1.6万元,每套B型健身器材售价为1.5(1﹣n)万元.
(1)、求证: 是圆 的切线;(2)、若 为 的中点,求 的值;(3)、若 ,求圆 的半径.23. 为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有A,B两种型号的健身器材可供选择.(1)、劲松公司2015年每套A型健身器材的售价为2.5万元,经过连续两年降价,2017年每套售价为1.6万元,求每套A型健身器材年平均下降率n;(2)、2017年市政府经过招标,决定年内采购并安装劲松公司A,B两种型号的健身器材共80套,采购专项经费总计不超过112万元,采购合同规定:每套A型健身器材售价为1.6万元,每套B型健身器材售价为1.5(1﹣n)万元.①A型健身器材最多可购买多少套?
②安装完成后,若每套A型和B型健身器材一年的养护费分别是购买价的5%和15%,市政府计划支出10万元进行养护,问该计划支出能否满足一年的养护需要?
24. 在 中, , ,以 为边在 的另一侧作 ,点 为射线 上任意一点,在射线 上截取 ,连接 .
 (1)、如图1,当点 落在线段 的延长线上时,直接写出 的度数;(2)、如图2,当点 落在线段 (不含边界)上时, 与 于点 ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;(3)、在(2)的条件下,若 ,求 的最大值.25. 如图,在平面直角坐标系 中,以直线 为对称轴的抛物线 与直线 交于 , 两点,与 轴交于 ,直线 与 轴交于点 .
(1)、如图1,当点 落在线段 的延长线上时,直接写出 的度数;(2)、如图2,当点 落在线段 (不含边界)上时, 与 于点 ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;(3)、在(2)的条件下,若 ,求 的最大值.25. 如图,在平面直角坐标系 中,以直线 为对称轴的抛物线 与直线 交于 , 两点,与 轴交于 ,直线 与 轴交于点 . (1)、求抛物线的函数表达式;(2)、设直线 与抛物线的对称轴的交点为 , 是抛物线上位于对称轴右侧的一点,若 ,且 与 的面积相等,求点 的坐标;(3)、若在 轴上有且只有一点 ,使 ,求 的值.
(1)、求抛物线的函数表达式;(2)、设直线 与抛物线的对称轴的交点为 , 是抛物线上位于对称轴右侧的一点,若 ,且 与 的面积相等,求点 的坐标;(3)、若在 轴上有且只有一点 ,使 ,求 的值.