四川省成都市青羊区石室联中2019年中考数学一模考试试卷
试卷更新日期:2020-05-06 类型:中考模拟
一、选择题
-
1. 的相反数是( )A、-3 B、3 C、- D、2. 下列几何体的主视图是三角形的是( )A、
 B、
B、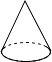 C、
C、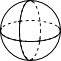 D、
D、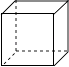 3. 习近平主席在2018年新年贺词中指出,2017年,基本医疗保险已经覆盖1350000000人.将1350000000用科学记数法表示为( )A、135×107 B、1.35×109 C、13.5×108 D、1.35×10144. 如图,直线l1∥l2∥l3 , 点A、B、C分别在直线l1、l2、l3上.若∠1=70°,∠2=50°,则∠ABC等于( )
3. 习近平主席在2018年新年贺词中指出,2017年,基本医疗保险已经覆盖1350000000人.将1350000000用科学记数法表示为( )A、135×107 B、1.35×109 C、13.5×108 D、1.35×10144. 如图,直线l1∥l2∥l3 , 点A、B、C分别在直线l1、l2、l3上.若∠1=70°,∠2=50°,则∠ABC等于( ) A、95° B、100° C、110° D、120°5. 函数 中自变量 的取值范围是( )A、 B、 C、 D、6. 某中学篮球队12名队员的年龄情况如下表:
A、95° B、100° C、110° D、120°5. 函数 中自变量 的取值范围是( )A、 B、 C、 D、6. 某中学篮球队12名队员的年龄情况如下表:年龄/岁
12
13
14
15
16
人数
1
3
4
2
2
关于这12名队员的年龄,下列说法中正确的是( )
A、众数为14 B、极差为3 C、中位数为13 D、平均数为147. 如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是( )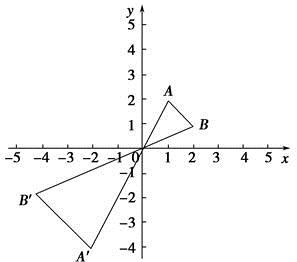 A、(2,4) B、(-1,-2) C、(-2,-4) D、(-2,-1)8. 若一元二次方程
A、(2,4) B、(-1,-2) C、(-2,-4) D、(-2,-1)8. 若一元二次方程 有实数解,则m的取值范围是( ) A、 B、 C、 D、9. 如图,PA、PB是⊙O的切线,切点分别为A、B , 若OA=2,∠P=60°,则 的长为( )
有实数解,则m的取值范围是( ) A、 B、 C、 D、9. 如图,PA、PB是⊙O的切线,切点分别为A、B , 若OA=2,∠P=60°,则 的长为( ) A、 π B、π C、 D、10. 抛物线 (对称轴为 )的图象如图所示,下列四个判断中正确的是( )
A、 π B、π C、 D、10. 抛物线 (对称轴为 )的图象如图所示,下列四个判断中正确的是( ) A、 , , B、 C、 D、
A、 , , B、 C、 D、二、填空题
-
11. 分解因式:m2n - n3=.12. 如图,四边形 与四边形 位似,其位似中心为点 ,且 ,则 .
 13. 方程 的解为.14. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=5,分别以点A、B为圆心,大于 AB的长为半径画弧,两弧交点分别为点P、Q,过P、Q两点作直线交BC于点D,则CD的长是.
13. 方程 的解为.14. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=5,分别以点A、B为圆心,大于 AB的长为半径画弧,两弧交点分别为点P、Q,过P、Q两点作直线交BC于点D,则CD的长是.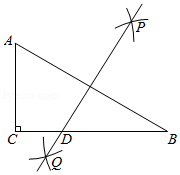 15. 已知x,y满足方程组 ,则 的值为.16. 如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=3,BE=2,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为 .
15. 已知x,y满足方程组 ,则 的值为.16. 如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=3,BE=2,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为 . 17. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1…按这样的规律进行下去,第1个正方形的面积为;第4个正方形的面积为 .
17. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1…按这样的规律进行下去,第1个正方形的面积为;第4个正方形的面积为 . 18. 如图,△ABC内接于⊙O.AB为⊙O的直径,BC=3,AB=5,D、E分别是边AB、BC上的两个动点(不与端点A、B、C重合),将△BDE沿DE折叠,点B的对应点B′恰好落在线段AC上(包含端点A、C),若△ADB′为等腰三角形,则AD的长为 .
18. 如图,△ABC内接于⊙O.AB为⊙O的直径,BC=3,AB=5,D、E分别是边AB、BC上的两个动点(不与端点A、B、C重合),将△BDE沿DE折叠,点B的对应点B′恰好落在线段AC上(包含端点A、C),若△ADB′为等腰三角形,则AD的长为 .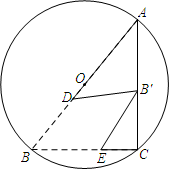 19. 如图,直线y=2x+b与双曲线y= (k>0)交于点A、D,直线AD交y轴、x轴于点B、C,直线y=- +n过点A,与双曲线y= (k>0)的另一个交点为点E,连接BE、DE,若S△ABE=4,且S△ABE:S△DBE=3:4,则k的值为 .
19. 如图,直线y=2x+b与双曲线y= (k>0)交于点A、D,直线AD交y轴、x轴于点B、C,直线y=- +n过点A,与双曲线y= (k>0)的另一个交点为点E,连接BE、DE,若S△ABE=4,且S△ABE:S△DBE=3:4,则k的值为 .
三、计算题
-
20.(1)、计算:(2)、化简:21. 已知关于 的一元二次方程 ,若方程的一个根为2,求 的值和方程的另一个根.
四、综合题
-
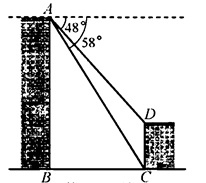
22. 如图,甲、乙两座建筑物的水平距离 为 ,从甲的顶部 处测得乙的顶部 处的俯角为 ,测得底部 处的俯角为 ,求甲、乙建筑物的高度 和 (结果取整数).参考数据: , .
 23. 我国中小学生迎来了新版“教育部统编义务教育语文教科书”,本次“统编本”教材最引人关注的变化之一是强调对传统文化经典著作的阅读.某校对 《三国演义》、 《红楼梦》、 《西游记》、 《水浒》四大名著开展“最受欢迎的传统文化经典著作”调查,随机调查了若干名学生(每名学生必选且只能选这四大名著中的一部)并将得到的信息绘制了下面两幅不完整的统计图:
23. 我国中小学生迎来了新版“教育部统编义务教育语文教科书”,本次“统编本”教材最引人关注的变化之一是强调对传统文化经典著作的阅读.某校对 《三国演义》、 《红楼梦》、 《西游记》、 《水浒》四大名著开展“最受欢迎的传统文化经典著作”调查,随机调查了若干名学生(每名学生必选且只能选这四大名著中的一部)并将得到的信息绘制了下面两幅不完整的统计图: (1)、本次一共调查了名学生;(2)、请将条形统计图补充完整;(3)、某班语文老师想从这四大名著中随机选取两部作为学生暑期必读书籍,请用树状图或列表的方法求恰好选中《三国演义》和《红楼梦》的概率.24. 如图,在平面直角坐标系中,直线 与反比例函数 在第一象限内的图象相交于点 .
(1)、本次一共调查了名学生;(2)、请将条形统计图补充完整;(3)、某班语文老师想从这四大名著中随机选取两部作为学生暑期必读书籍,请用树状图或列表的方法求恰好选中《三国演义》和《红楼梦》的概率.24. 如图,在平面直角坐标系中,直线 与反比例函数 在第一象限内的图象相交于点 . (1)、求反比例函数的解析式;(2)、将直线 向上平移后与反比例函数图象在第一象限内交于点 ,与 轴交于点 ,且 的面积为 ,求直线 的解析式.25. 如图,AB为⊙O的直径,AC,BC是⊙O的两条弦,过点C作∠BCD=∠A,CD交AB的延长线与点D.
(1)、求反比例函数的解析式;(2)、将直线 向上平移后与反比例函数图象在第一象限内交于点 ,与 轴交于点 ,且 的面积为 ,求直线 的解析式.25. 如图,AB为⊙O的直径,AC,BC是⊙O的两条弦,过点C作∠BCD=∠A,CD交AB的延长线与点D. (1)、求证:CD是⊙O的切线;(2)、若tanA= ,求 的值;(3)、在(2)的条件下,若AB=7,∠CED=∠A+∠EDC,求EC与ED的长.26. 某商店购进一批单价为8元的商品,如果按每件10元出售,那么每天可销售100件,经调查发现,这种商品的销售单价每提高1元,其销售量相应减少10件.(1)、求销售量 件与销售单价 元之间的关系式;(2)、当销售单价 定为多少,才能使每天所获销售利润最大?最大利润是多少?27. 如图,在菱形ABCD中,对角线AC、BD交于点O,已知AC=2 ,AB=5.
(1)、求证:CD是⊙O的切线;(2)、若tanA= ,求 的值;(3)、在(2)的条件下,若AB=7,∠CED=∠A+∠EDC,求EC与ED的长.26. 某商店购进一批单价为8元的商品,如果按每件10元出售,那么每天可销售100件,经调查发现,这种商品的销售单价每提高1元,其销售量相应减少10件.(1)、求销售量 件与销售单价 元之间的关系式;(2)、当销售单价 定为多少,才能使每天所获销售利润最大?最大利润是多少?27. 如图,在菱形ABCD中,对角线AC、BD交于点O,已知AC=2 ,AB=5. (1)、求BD的长;(2)、点E为直线AD上的一个动点,连接CE,将线段EC绕点C顺时针旋转∠BCD的角度后得到对应的线段CF(即∠ECF=∠BCD),EF交CD于点P.
(1)、求BD的长;(2)、点E为直线AD上的一个动点,连接CE,将线段EC绕点C顺时针旋转∠BCD的角度后得到对应的线段CF(即∠ECF=∠BCD),EF交CD于点P.①当E为AD的中点时,求EF的长;
②连接AF、DF,当DF的长度最小时,求△ACF的面积.
28. 如图1,在平面直角坐标系xOy中,抛物线y=-(x-a)(x-4)(a<0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点. (1)、若D点坐标为( ),求抛物线的解析式和点C的坐标;(2)、若点M为抛物线对称轴上一点,且点M的纵坐标为a,点N为抛物线在x轴上方一点,若以C、B、M、N为顶点的四边形为平行四边形时,求a的值;(3)、直线y=2x+b与(1)中的抛物线交于点D、E(如图2),将(1)中的抛物线沿着该直线方向进行平移,平移后抛物线的顶点为D′,与直线的另一个交点为E′,与x轴的交点为B′,在平移的过程中,求D′E′的长度;当∠E′D′B′=90°时,求点B′的坐标.
(1)、若D点坐标为( ),求抛物线的解析式和点C的坐标;(2)、若点M为抛物线对称轴上一点,且点M的纵坐标为a,点N为抛物线在x轴上方一点,若以C、B、M、N为顶点的四边形为平行四边形时,求a的值;(3)、直线y=2x+b与(1)中的抛物线交于点D、E(如图2),将(1)中的抛物线沿着该直线方向进行平移,平移后抛物线的顶点为D′,与直线的另一个交点为E′,与x轴的交点为B′,在平移的过程中,求D′E′的长度;当∠E′D′B′=90°时,求点B′的坐标.