四川省成都市郫都区2019年中考数学一模考试试卷

试卷更新日期：2020-05-06 类型：中考模拟

进入出卷网下载

一、选择题

1. 《习近平总书记系列重要讲话读本》中讲到“绿水青山就是金山银山”，我们要尊重自然、顺应自然、保护自然的理念，贯彻节约资源和保护环境的基本国策．在下列环保标志中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（）

A、a⁴+a⁴=a⁸ B、a⁵•a⁴=a²⁰ C、a⁴÷a=a³ D、（-a³）²=a⁵

查看试题解析
3. 中国高速路里程已突破13万公里，居世界第一位，将13万用科学记数法表示为（）

A、 $0.13 \times 10^{5}$ B、 $1.3 \times 10^{4}$ C、 $1.3 \times 10^{5}$ D、 $13 \times 10^{4}$

查看试题解析
4. 把方程x﹣4x＝4的解用数轴上的点表示出来，那么该点在图中的（）

A、点M ，点N之间 B、点N ，点O之间 C、点O ，点P之间 D、点P ，点Q之间

查看试题解析
5. 如图，是一个几何体的三视图，则这个几何体是（）

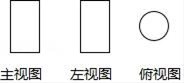A、长方体 B、圆柱体 C、球体 D、圆锥体

查看试题解析
6. 某校组织“国学经典”诵读比赛，参赛10名选手的得分情况如表所示：

分数/分

80

85

90

95

人数/人

3

4

2

1

那么，这10名选手得分的中位数和众数分别是（）

A、85.5和80 B、85.5和85 C、85和82.5 D、85和85

查看试题解析
7. 已知点（﹣2，y₁），（﹣1，y₂），（1，y₃）都在直线y＝﹣x+b上，则y₁ ， y₂ ， y₃的值的大小关系是（）

A、y₁＞y₂＞y₃ B、y₁＜y₂＜y₃ C、y₃＞y₁＞y₂ D、y₂＞y₁＞y₃

查看试题解析
8. 如图，在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=6，AB=5，则AE的长为（）

A、4 B、8 C、6 D、10

查看试题解析
9. 三角形的外心是指什么线的交点？（）

A、三边中线 B、三内角的平分线 C、三边高线 D、三边垂直平分线

查看试题解析
10. 如图，池中心竖直水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，水管的长为（）

A、2.1m B、2.2m C、2.3m D、2.25m

查看试题解析

二、填空题

11. 计算： ${(\frac{1}{2})}^{- 3}$ ＝.

查看试题解析
12. 如图，将香港特别行政区标志紫荆花图案绕中心旋转，当此图案第一次与自身重合时，其旋转角的大小为．

查看试题解析
13. 如图，将△ABC沿BC边上的中线AD平移到△A′B′C′的位置，已知△ABC的面积为18，阴影部分三角形的面积为8，若AA′=1，则A′D的值为．

查看试题解析
14. 如果关于 $x$ 的一元二次方程 $(m - 2) x^{2} + 2 x + 1 = 0$ 有两个不相等的实数根，那么 $m$ 的取值范围为.

查看试题解析
15. 如图，已知矩形OABC与矩形ODEF是位似图形，P是位似中心，若点B的坐标为 $(2 ， 4)$ ，点E的坐标为 $(- 1 ， 2)$ ，则点P的坐标为．

查看试题解析
16. 设α、β是方程x²-x-2018=0的两根，则α³+2019β-2018的值为．

查看试题解析
17. 从-2，-1，0，1，2这5个数中随机抽取一个数记为a，则使直线 $y = \frac{1}{4} x - a$ 与双曲线 $y = \frac{3 a + 2}{x}$ 有1个交点的概率为．

查看试题解析
18. 在△ABC中，∠ACB＝90°，BC＝8，AC＝6，以点C为圆心，4为半径的圆上有一动点D，连接AD，BD，CD，则 $\frac{1}{2}$ BD+AD的最小值是．

查看试题解析
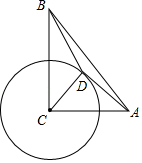19. 对于一个函数，如果它的自变量 x 与函数值 y 满足：当−1≤x≤1 时，−1≤y≤1，则称这个函数为“闭函数”.例如：y=x，y=−x 均是“闭函数”. 已知 y = ax²+ bx + c(a≠0) 是“闭函数”，且抛物线经过点 A(1，−1)和点 B(−1，1)，则 a 的取值范围是.

查看试题解析

三、计算题

20.

(1)、计算：3tan30°- $\sqrt{12} - \sqrt{2} cos 45 ^{\circ} + {(π - 2019)}^{0}$

(2)、化简： $\frac{m^{2} + 2 m + 1}{m^{2} + 2 m} \div (1 - \frac{1}{m + 2})$

查看试题解析
21. 解不等式组： ${\begin{matrix} 3 x + 4 \geq 2 x \\ \frac{x + 2}{5} - \frac{x - 3}{4} \geq 1 \end{matrix}$

查看试题解析

四、综合题

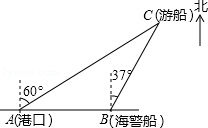
22. 一艘观光游船从港口A以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里每小时的速度前往救援，求海警船到大事故船C处所需的大约时间．（温馨提示：sin53°≈0.8，cos53°≈0.6）

查看试题解析
23. 一个不透明的口袋里装有分别标有汉字“美”、“丽”、“光”、“明”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球.

(1)、若从中任取一个球，求摸出球上的汉字刚好是“美”的概率；

(2)、甲从中任取一球，不放回，再从中任取一球，请用树状图或列表法，求甲取出的两个球上的汉字恰能组成“美丽”或“光明”的概率.

查看试题解析
24. 如图，直线y₁=k₁x+b与双曲线 $y_{2} = \frac{k_{2}}{x}$ 在第一象限内交于A、B两点，已知A(1，m)，B(2，1)．

(1)、直接写出不等式y₂＞y₁的解集；

(2)、求直线AB的解析式；

(3)、设点P是线段AB上的一个动点，过点P作PD⊥x轴于点D，E是y轴上一点，求△PED的面积S的最大值．

查看试题解析
25. 某商店准备购进一批电冰箱和空调，每台电冰箱的进价比每台空调的进价多400元，商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等．

(1)、求每台电冰箱与空调的进价分别是多少？

(2)、已知电冰箱的销售价为每台2100元，空调的销售价为每台1750元．若商店准备购进这两种家电共100台，其中购进电冰箱x台（33≤x≤40），那么该商店要获得最大利润应如何进货？

查看试题解析
26. 如图，点E是正方形ABCD的边BC延长线上一点，连接DE ，过顶点B作BF⊥DE ，垂足为F ， BF交边DC于点G ．

(1)、求证：DG•BC＝DF•BG；

(2)、连接CF ，求∠CFB的大小；

(3)、作点C关于直线DE的对称点H ，连接CH ， FH ．猜想线段DF ， BF ， CH之间的数量关系并加以证明．

查看试题解析
27. 如图，抛物线y=-x²+mx+2m²（m＞0）与x轴交于A、B两点，点A在点B的左边，C是抛物线上一个动点（点C与点A、B不重合），D是OC的中点，连接BD并延长，交AC于点E．

(1)、用含m的代数式表示点A、B的坐标；

(2)、求证： $\frac{CE}{AE} = \frac{2}{3}$ ；

(3)、若点C、点A到y轴的距离相等，且s_△CDE=1.6时，求抛物线和直线BE的解析式．

查看试题解析
28. 如图，在△ABC中，∠C=90°，∠ABC的平分线交AC于点E，过点E作BE的垂线交AB于点F，⊙O是△BEF的外接圆．

(1)、求证：AC是⊙O的切线；

(2)、过点E作EH⊥AB，垂足为H，求证：CD=HF；

(3)、若CD=1，EF= $\sqrt{10}$ ，求AF长．

查看试题解析

分数/分	80	85	90	95
人数/人	3	4	2	1