四川省成都市2019年中考数学二模考试试卷
试卷更新日期:2020-05-06 类型:中考模拟
一、选择题
-
1. 下列各组数中,互为倒数的是( )A、 与 B、 与 C、 与 D、 与2. 如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. “神舟七号”舱门除了有气压外,还有光压,开门最省力也需要用大约568000斤的臂力.用科学记数法表示568000是( )A、568×103 B、56.8×104 C、5.68×105 D、0.568×1064. 下列说法中,正确的是( )A、不可能事件发生的概率为0 B、随机事件发生的概率为 C、概率很小的事件不可能发生 D、投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次5. 如图, 中,对角线 , 相交于点 ,添加下列条件不能判定 是菱形的是( )
3. “神舟七号”舱门除了有气压外,还有光压,开门最省力也需要用大约568000斤的臂力.用科学记数法表示568000是( )A、568×103 B、56.8×104 C、5.68×105 D、0.568×1064. 下列说法中,正确的是( )A、不可能事件发生的概率为0 B、随机事件发生的概率为 C、概率很小的事件不可能发生 D、投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次5. 如图, 中,对角线 , 相交于点 ,添加下列条件不能判定 是菱形的是( ) A、 B、 C、 D、6. 下列选项中,能使关于x的一元二次方程ax2﹣4x+c=0一定有实数根的是( )A、a>0 B、a=0 C、c>0 D、c=07. 如图,将长方形纸片ABCD沿BD折叠,得到△ , 与AB交于点E,若∠1=35°,则∠2的度数为( )
A、 B、 C、 D、6. 下列选项中,能使关于x的一元二次方程ax2﹣4x+c=0一定有实数根的是( )A、a>0 B、a=0 C、c>0 D、c=07. 如图,将长方形纸片ABCD沿BD折叠,得到△ , 与AB交于点E,若∠1=35°,则∠2的度数为( )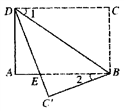 A、30° B、20° C、35° D、55°8. 如图,已知直线 则 ( )
A、30° B、20° C、35° D、55°8. 如图,已知直线 则 ( ) A、 B、 C、 D、9. 如图,在 中,已知 ,则 的度数为( )
A、 B、 C、 D、9. 如图,在 中,已知 ,则 的度数为( )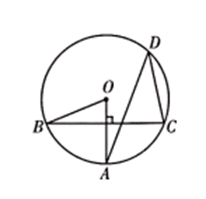 A、 B、 C、 D、10. 如图,矩形AOBC的面积为4,反比例函数 的图象的一支经过矩形对角线的交点P,则该反比例函数的解析式是( )
A、 B、 C、 D、10. 如图,矩形AOBC的面积为4,反比例函数 的图象的一支经过矩形对角线的交点P,则该反比例函数的解析式是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式:xy2﹣2xy+x= .12. 如图,在△ABC中,AB=AC,BD平分∠ABC,交AC于点D.若BD=BC,则∠A=度.
 13. 如图,在菱形 中,已知 则菱形 的面积为 .
13. 如图,在菱形 中,已知 则菱形 的面积为 . 14. 如图,已知 为原点,点 的坐标为 ,点 的坐标为 过 三点,点 为优弧 上一点(不与点 重合),则 的值为 .
14. 如图,已知 为原点,点 的坐标为 ,点 的坐标为 过 三点,点 为优弧 上一点(不与点 重合),则 的值为 . 15. 计算:16. 解方程式: - 3 =17. 我市某校开展了以“梦想中国”为主题的摄影大赛,要求参赛学生每人交一件作品.现将从中挑选的50件参赛作品的成绩(单位:分)统计如下:
15. 计算:16. 解方程式: - 3 =17. 我市某校开展了以“梦想中国”为主题的摄影大赛,要求参赛学生每人交一件作品.现将从中挑选的50件参赛作品的成绩(单位:分)统计如下:等级
成绩(用m表示)
频数
频率
A
90≤ m ≤100
x
0.08
B
80≤ m <90
34
y
C
m <80
12
0.24
合计

50
1
请根据上表提供的信息,解答下列问题:
(1)、表中 的值为 , 的值为;(直接填写结果)(2)、将本次参赛作品获得A等级的学生依次用A1、A2、A3……表示.现该校决定从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,则恰好抽到学生A1和A2的概率为 . (直接填写结果)18. 如图,在教学楼距地面 米高的窗口中 处,测得正前方旗杆顶部 点的仰角为 旗杆底部 点的俯角为 .升旗时,国旗上端悬挂在距地面 米处.若国旗随国歌声冉冉升起,并在国歌播放 秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升? (参考数据: ) 19. 如图,一次函数y=kx+b的图象分别与反比例函数 的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.
19. 如图,一次函数y=kx+b的图象分别与反比例函数 的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB. (1)、求函数y=kx+b和 的表达式;(2)、已知点C(0,10),试在该一次函数图象上确定一点M,使得MB=MC。求此时点M的坐标.20. 如图,点A、B、C、D是直径为AB的⊙O上的四个点,CD=BC,AC与BD交于点E。
(1)、求函数y=kx+b和 的表达式;(2)、已知点C(0,10),试在该一次函数图象上确定一点M,使得MB=MC。求此时点M的坐标.20. 如图,点A、B、C、D是直径为AB的⊙O上的四个点,CD=BC,AC与BD交于点E。 (1)、求证:DC2=CE·AC;
(1)、求证:DC2=CE·AC;
(2)、若AE=2EC,求 之值;
(3)、在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,若S△ACH= ,求EC之长.21. 若mn=m+3,则2mn+3m-5nm+10=.22. 如图,已知 是 的直径, 是 的弦,过点 作 的切线,与 的延长线交于点 作 交直线 于点 .若 则 . 23. 如图,在矩形 中,已知 将矩形 折叠,使点 与点 重合,折痕为 连接 的面积与 的面积比为 ,则 的值为 .
23. 如图,在矩形 中,已知 将矩形 折叠,使点 与点 重合,折痕为 连接 的面积与 的面积比为 ,则 的值为 . 24. 如图,△ABC中,AB=AC,D是AB上的一点,且AD= AB,DF∥BC,E为BD的中点.若EF⊥AC,BC=6,则四边形DBCF的面积为 .
24. 如图,△ABC中,AB=AC,D是AB上的一点,且AD= AB,DF∥BC,E为BD的中点.若EF⊥AC,BC=6,则四边形DBCF的面积为 . 25. 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB= ,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为 .
25. 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB= ,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为 . 26. 鄂州某个体商户购进某种电子产品的进价是50元/个,根据市场调研发现售价是80元/个时,每周可卖出160个,若销售单价每个降低2元,则每周可多卖出20个.设销售价格每个降低x元(x为偶数),每周销售为y个.(1)、直接写出销售量y个与降价x元之间的函数关系式;(2)、设商户每周获得的利润为W元,当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?(3)、若商户计划下周利润不低于5200元的情况下,他至少要准备多少元进货成本?27. 在矩形ABCD中,AB=8,AD=12,M是AD边的中点,P是AB边上的一个动点(不与A、B重合),PM的延长线交射线CD于Q点,MN⊥PQ交射线BC于N点。
26. 鄂州某个体商户购进某种电子产品的进价是50元/个,根据市场调研发现售价是80元/个时,每周可卖出160个,若销售单价每个降低2元,则每周可多卖出20个.设销售价格每个降低x元(x为偶数),每周销售为y个.(1)、直接写出销售量y个与降价x元之间的函数关系式;(2)、设商户每周获得的利润为W元,当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?(3)、若商户计划下周利润不低于5200元的情况下,他至少要准备多少元进货成本?27. 在矩形ABCD中,AB=8,AD=12,M是AD边的中点,P是AB边上的一个动点(不与A、B重合),PM的延长线交射线CD于Q点,MN⊥PQ交射线BC于N点。
(1)、若点N在BC之间时,如图:
①求证:∠NPQ=∠PQN;②请问 是否为定值?若是定值,求出该定值;若不是,请举反例说明;
(2)、当△PBN与△NCQ的面积相等时,求AP的值.28. 如图,已知直线 与 轴和 轴分别交于点 和点 抛物线 经过点 与直线 的另一个交点为 .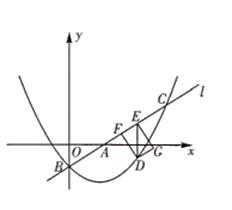 (1)、求 的值和抛物线的解析式(2)、点 在抛物线上, 轴交直线 于点 点 在直线 上,且四边形 为矩形.设点 的横坐标为 矩形 的周长为 求 与 的函数关系式以及 的最大值(3)、将 绕平面内某点 逆时针旋转 得到 (点 分别与 点对应),若 的两个顶点恰好落在抛物线上,请直接写出点 的坐标.
(1)、求 的值和抛物线的解析式(2)、点 在抛物线上, 轴交直线 于点 点 在直线 上,且四边形 为矩形.设点 的横坐标为 矩形 的周长为 求 与 的函数关系式以及 的最大值(3)、将 绕平面内某点 逆时针旋转 得到 (点 分别与 点对应),若 的两个顶点恰好落在抛物线上,请直接写出点 的坐标.