四川省成都市大邑县2019年中考数学一模考试试卷
试卷更新日期:2020-05-06 类型:中考模拟
一、选择题
-
1. 给出四个实数 ,2, ,﹣2,其中最小的数是( )A、 B、2 C、 D、﹣22. 四川省公布了2018年经济数据GDP排行榜,成都市排名全省第一,GDP总量为15342亿元,数据“15342亿元”用科学记数法表示为( )A、1.5342×104亿元 B、15.342×103亿元 C、153.42×102亿元 D、0.15342×105亿元3. 如图所示的正六棱柱的左视图是( )
 A、
A、 B、
B、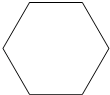 C、
C、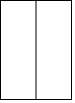 D、
D、 4. 在平面直角坐标系中,点P(2,﹣5)关于坐标原点对称的点的坐标是( )A、(2,﹣5) B、(﹣2,5) C、(2,5) D、(﹣2,﹣5)5. 下列计算正确的是( )A、2x2•3x3=6x6 B、(﹣y2)3=﹣y6 C、2y3﹣6y2=﹣4y D、(y﹣2)2=y2﹣46. 如图,已知AB=DC,需添加下列( )条件后,就一定能判定△ABC≌△DCB.
4. 在平面直角坐标系中,点P(2,﹣5)关于坐标原点对称的点的坐标是( )A、(2,﹣5) B、(﹣2,5) C、(2,5) D、(﹣2,﹣5)5. 下列计算正确的是( )A、2x2•3x3=6x6 B、(﹣y2)3=﹣y6 C、2y3﹣6y2=﹣4y D、(y﹣2)2=y2﹣46. 如图,已知AB=DC,需添加下列( )条件后,就一定能判定△ABC≌△DCB. A、AO=BO B、∠ACB=∠DBC C、AC=DB D、BO=CO7. 某同学参加了学校举行的“五好小公民•红旗飘飘”演讲比赛,七名评委给该同学的打分(单位:分)情况如表:
A、AO=BO B、∠ACB=∠DBC C、AC=DB D、BO=CO7. 某同学参加了学校举行的“五好小公民•红旗飘飘”演讲比赛,七名评委给该同学的打分(单位:分)情况如表:评委
评委1
评委2
评委3
评委4
评委5
评委6
评委7
打分
6
8
7
8
5
7
8
关于七名评委给该同学的打分下列说法不正确的是( )
A、中位数是8分 B、众数是8分 C、极差是3分 D、平均数是7分8. 关于分式方程 的解,下列说法正确的是( )A、解是x=2 B、解是x=4 C、解是x=﹣4 D、无解9. 如图,AB是⊙O的弦,OC⊥AB,交⊙O于点C,连接OA,OB,BC,若∠ABC=20°,则∠BAO的度数是( )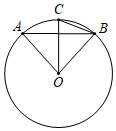 A、40° B、45° C、50° D、55°10. 关于二次函数y=﹣3x2+6x+1,以下说法不正确的是( )A、图象与y轴的交点坐标为(0,1) B、图象的对称轴在y轴的右侧 C、当x>0时,y的值随x值的增大而减小 D、y的最大值为4
A、40° B、45° C、50° D、55°10. 关于二次函数y=﹣3x2+6x+1,以下说法不正确的是( )A、图象与y轴的交点坐标为(0,1) B、图象的对称轴在y轴的右侧 C、当x>0时,y的值随x值的增大而减小 D、y的最大值为4二、填空题
-
11. 分解因式: = .12. 如图,在△ABC 中,AB=AC,点 D 是△ABC 的边 AC 延长线于一点, 且 CB=CD,连结 BD,若∠A=28°,则∠CBD 的度数为 .
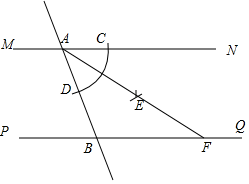
 13. 已知点A(x1 , y1),B(x2 , y2)在直线y=kx+b上,且直线经过第一,二,三象限,当x1>x2时,y1与y2的大小关系是 .14. 如图,直线MN∥PQ , 直线AB分别与MN , PQ相交于点A , B . 小宇同学利用以下步骤作图:
13. 已知点A(x1 , y1),B(x2 , y2)在直线y=kx+b上,且直线经过第一,二,三象限,当x1>x2时,y1与y2的大小关系是 .14. 如图,直线MN∥PQ , 直线AB分别与MN , PQ相交于点A , B . 小宇同学利用以下步骤作图:①以点A为圆心,适当长为半径作弧交射线AN于点C , 交线段AB于点D;
②以点C为圆心,适当长为半径画弧;然后再以点D为圆心,同样长为半径画弧.前后两弧在∠NAB内交于点E;
③作射线AE , 交PQ于点F;
若AF=2 ,∠FAN=30°,则线段BF的长为 .
三、计算题
-
15. 计算(1)、计算: .(2)、化简: .16. 若关于y的一元二次方程by2﹣(2b﹣1)y+b=0有两个实数根,求满足条件的最大整数b .
四、综合题
-
17. 某校九年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,数据整理过程如下,请完成下面数据整理中的问题:
①收集数据
从甲、乙两个班中各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班:65,75,75,80,60,50,75,90,85,65;
乙班:90,55,80,70,55,70,95,80,65,70;
②整理描述数据
按如下分数段整理、描述这两组样本数据:
成绩x
人数
班级
50≤x<60
60≤x<70
70≤x<80
80≤x<90
90≤x<100
甲班
1
3
3
2
1
乙班
2
1
m
2
n
(1)、在表中:m= , n=;(2)、分析数据若规定测试成绩在80分(含80分)以上的学生身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有人;
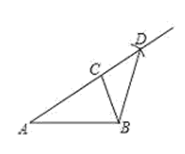
(3)、现从甲班指定的3名学生(1男2女),乙班指定的2名学生(1男1女)中分别抽取1名学生去参加身体素质拓展训练,用树状图或列表法求出抽到的2名同学中恰好是1男1女的概率.18. 一艘货轮以34海里/时的速度在海面上向正南方向航行,当它行驶至B处时,某观察者发现在货轮的北偏东75°方向有一灯塔C;货轮继续向南航行1.5小时后到达A处,某观察者再次发现灯塔C在货轮的东北方向.求此时货轮与灯塔C的距离.(结果保留到个位)(参考数据:sin75°≈0.97,cos75°≈0.29,tan75°≈3.73,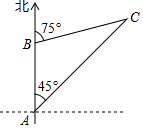 19. 如图,在平面直角坐标系xOy中,一次函数y=﹣x+2的图象与x轴交于点A与反比例函数 (x<0)的图象交于点B , 过点B作BC⊥x轴于点C , 且OA=OC .
19. 如图,在平面直角坐标系xOy中,一次函数y=﹣x+2的图象与x轴交于点A与反比例函数 (x<0)的图象交于点B , 过点B作BC⊥x轴于点C , 且OA=OC .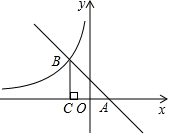 (1)、求点A的坐标和反比例函数的表达式;(2)、若点P是反比例函数 (x<0)的图象上的点,过P作PQ∥y轴,交直线AB于点Q , 当PQ=BC时,求点P的坐标.20. 如图所示,AB是⊙O的直径,点C是弧AB的中点,点D是弧BC的中点,连接AC , BC , AD , BD , 且AD与BC相交于点F , 延长AC至E , 使AC=EC , 连接EB交AD的延长线于点G .
(1)、求点A的坐标和反比例函数的表达式;(2)、若点P是反比例函数 (x<0)的图象上的点,过P作PQ∥y轴,交直线AB于点Q , 当PQ=BC时,求点P的坐标.20. 如图所示,AB是⊙O的直径,点C是弧AB的中点,点D是弧BC的中点,连接AC , BC , AD , BD , 且AD与BC相交于点F , 延长AC至E , 使AC=EC , 连接EB交AD的延长线于点G .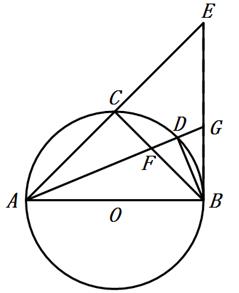 (1)、求证:EB是⊙O的切线;(2)、求证;AF=2BD;(3)、求证:线段BG是线段CF和线段EG的比例中项.21. 已知点A(a , b)既在一次函数y=﹣x+3的图象上,又在反比例函数 的图象上,则代数式a2+b2的值为 .22. 刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用圆内接或外切正多边形逐步逼近圆来近似计算圆的面积.下图是其中的一个图形,六边形ABCDEF是⊙O的外切正六边形,现随机向该图形掷一枚小针,则针尖落在⊙O内的概率是 . (结果不取近似值).
(1)、求证:EB是⊙O的切线;(2)、求证;AF=2BD;(3)、求证:线段BG是线段CF和线段EG的比例中项.21. 已知点A(a , b)既在一次函数y=﹣x+3的图象上,又在反比例函数 的图象上,则代数式a2+b2的值为 .22. 刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用圆内接或外切正多边形逐步逼近圆来近似计算圆的面积.下图是其中的一个图形,六边形ABCDEF是⊙O的外切正六边形,现随机向该图形掷一枚小针,则针尖落在⊙O内的概率是 . (结果不取近似值).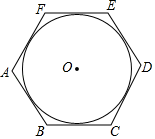 23. 若常数a能使关于x的不等式组 有解,且使关于y的方程 的解为非负数,则符合条件的所有整数a的和为 .24. 如图在菱形纸片ABCD中,AB=4,∠B=120°,将菱形纸片翻折,使点A落在边CD的中点G处,折痕为EF , 点E , F分别在边AD , AB上,则sin∠GEF的值为 .
23. 若常数a能使关于x的不等式组 有解,且使关于y的方程 的解为非负数,则符合条件的所有整数a的和为 .24. 如图在菱形纸片ABCD中,AB=4,∠B=120°,将菱形纸片翻折,使点A落在边CD的中点G处,折痕为EF , 点E , F分别在边AD , AB上,则sin∠GEF的值为 . 25. 如图,已知点B(0,2),A(﹣6,﹣1)在反比例函数 的图象上,作射线AB , 再将射线AB绕点A逆时针旋转45°后,交反比例函数 图象于点C , 则点C的坐标为 .
25. 如图,已知点B(0,2),A(﹣6,﹣1)在反比例函数 的图象上,作射线AB , 再将射线AB绕点A逆时针旋转45°后,交反比例函数 图象于点C , 则点C的坐标为 . 26. 成都市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种新产品的成本为30元/件,经市场调查发现,该产品的年销售量y(万件)与销售单价x(元)之间的函数关系如下图:
26. 成都市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种新产品的成本为30元/件,经市场调查发现,该产品的年销售量y(万件)与销售单价x(元)之间的函数关系如下图: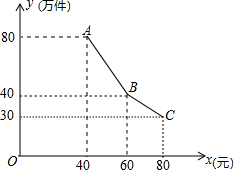 (1)、求出y与x之间的函数关系式;(2)、当该产品的售价为多少时,该企业销售该产品获得的年利润最大?最大年利润是多少?(注:年利润=年销售量×(销售单价﹣成本单价))27. 已知:点E是正方形ABCD中边AB的中点.
(1)、求出y与x之间的函数关系式;(2)、当该产品的售价为多少时,该企业销售该产品获得的年利润最大?最大年利润是多少?(注:年利润=年销售量×(销售单价﹣成本单价))27. 已知:点E是正方形ABCD中边AB的中点.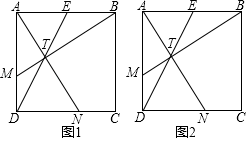 (1)、如图1,点T为线段DE上一点,连接BT并延长交AD于点M , 连接AT并延长交CD于点N , 且AM=DN . 试判断线段AN与线段BM的关系,并证明;求证:点M是线段AD的黄金分割点.(2)、如图2,在AD边上取一点M , 满足AM2=DM•DA时,连接BM交DE于点T , 连接AT并延长交DC于点N , 求tan∠MTD的值.28. 抛物线l1:y=x2+bx+c与它的对称轴x=﹣2交于点A , 且经过点B(0,﹣2).
(1)、如图1,点T为线段DE上一点,连接BT并延长交AD于点M , 连接AT并延长交CD于点N , 且AM=DN . 试判断线段AN与线段BM的关系,并证明;求证:点M是线段AD的黄金分割点.(2)、如图2,在AD边上取一点M , 满足AM2=DM•DA时,连接BM交DE于点T , 连接AT并延长交DC于点N , 求tan∠MTD的值.28. 抛物线l1:y=x2+bx+c与它的对称轴x=﹣2交于点A , 且经过点B(0,﹣2).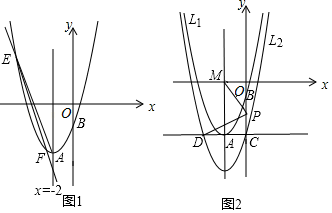 (1)、求抛物线l1的解析式;(2)、如图1,直线y=kx+2k﹣8(k<0)与抛物线l1交于点E , F , 若△AEF的面积为 ,求k的值;(3)、如图2,将抛物线l1向下平移n(n>0)个单位长度得到抛物线l2 , 抛物线l2与y轴交于点C , 过点C作x轴的平行线交抛物线l2于另一点D;抛物线l2的对称轴与x轴的交于点M , P为线段OC上一点,若△POM与△PCD相似,并且符合该条件的点P有且只有2个,求n的值及相应点P的坐标.
(1)、求抛物线l1的解析式;(2)、如图1,直线y=kx+2k﹣8(k<0)与抛物线l1交于点E , F , 若△AEF的面积为 ,求k的值;(3)、如图2,将抛物线l1向下平移n(n>0)个单位长度得到抛物线l2 , 抛物线l2与y轴交于点C , 过点C作x轴的平行线交抛物线l2于另一点D;抛物线l2的对称轴与x轴的交于点M , P为线段OC上一点,若△POM与△PCD相似,并且符合该条件的点P有且只有2个,求n的值及相应点P的坐标.