浙江省温州市2016-2017学年高一下学期期末数学考试试卷

试卷更新日期：2017-09-14 类型：期末考试

进入出卷网下载

一、选择题

1. sin480°=（）

A、 $- \frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 已知向量 $\vec{a}$ =（﹣1，2）， $\vec{b}$ =（2，m），若 $\vec{a}$ ∥ $\vec{b}$ ，则m=（）

A、﹣4 B、4 C、﹣1 D、1

查看试题解析
3. 已知sin（3π﹣α）= $\frac{2}{3}$ ，则sinα=（）

A、 $- \frac{2}{3}$ B、 $\frac{2}{3}$ C、﹣ $\frac{\sqrt{5}}{3}$ D、 $\frac{\sqrt{5}}{3}$

查看试题解析
4. 已知正方形ABCD的边长为1， $\vec{A B}$ =a， $\vec{B C}$ =b，则a+b的模等于（）

A、1 B、2 C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
5. 下列函数中，最小正周期为 $\frac{π}{2}$ 的是（）

A、y=|sinx| B、y=sinxcosx C、y=|tanx| D、y=cos4x

查看试题解析
6. 数列{a_n}满足a_n₊₁= $\frac{1}{a_{n} + 1}$ ，a₁=1，则 $\frac{a_{4}}{a_{5}}$ =（）

A、 $\frac{9}{10}$ B、 $\frac{3}{8}$ C、 $\frac{25}{24}$ D、 $\frac{24}{25}$

查看试题解析
7. 不等式 $\frac{1}{x}$ ＜﹣1的解集为（）

A、{x|﹣1＜x＜0} B、{x|x＜﹣1} C、{x|x＞﹣1} D、{x|x＜0}

查看试题解析
8. 已知cosθ=﹣ $\frac{3}{5}$ （ $\frac{π}{2}$ ＜θ＜π），则cos（ $θ - \frac{π}{3}$ ）=（）

A、 $\frac{4 \sqrt{3} + 3}{10}$ B、 $\frac{4 \sqrt{3} - 3}{10}$ C、﹣ $\frac{4 \sqrt{3} + 3}{10}$ D、 $\frac{4 - 3 \sqrt{3}}{10}$

查看试题解析
9. 已知x＞y＞z，且x+y+z=0，下列不等式中成立的是（）

A、y＞0 B、xz＞yz C、xy＞yz D、xy＞xz

查看试题解析
10. 设△ABC的内角A，B，C所对的边分别是a，b，c，且（2b﹣ $\sqrt{3}$ c）cosA= $\sqrt{3}$ acosC，则角A的大小为（）

A、 $\frac{π}{3}$ B、 $\frac{π}{6}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看试题解析
11. 函数y=cos2x的图象向右平移φ（0＜φ＜ $\frac{π}{2}$ ）个单位后，与函数y=sin（2x﹣ $\frac{π}{6}$ ）的图象重合，则φ=（）

A、 $\frac{π}{12}$ B、 $\frac{π}{6}$ C、 $\frac{π}{3}$ D、 $\frac{5 π}{12}$

查看试题解析
12. 已知tanα=2，tan（α﹣β）=﹣3，则tanβ=（）

A、﹣1 B、1 C、 $\frac{1}{7}$ D、5

查看试题解析
13. 将函数y=2cos（x﹣ $\frac{π}{3}$ ）的图象上所有的点的横坐标缩短到原来的 $\frac{1}{2}$ 倍（纵坐标不变），得到函数y=g（x）的图象，则函数y=g（x）的图象（）

A、关于点（﹣ $\frac{π}{6}$ ，0）对称 B、关于点（ $\frac{5 π}{12}$ ，0）对称 C、关于直线x=﹣ $\frac{π}{6}$ 对称 D、关于直线x= $\frac{5 π}{12}$ 对称

查看试题解析
14. 等差数列{a_n}的前n项和为S_n ，若S₉=45，则3a₄+a₈=（）

A、10 B、20 C、35 D、45

查看试题解析
15. 设变量x，y满足约束条件 ${\begin{matrix} x - y + 2 \geq 0 \\ 2 x + 3 y - 6 \geq 0 \\ 3 x + 2 y - 9 \leq 0 \end{matrix}$ ，则目标函数z=4x+5y的最小值为（）

A、6 B、8 C、10 D、12

查看试题解析
16. 已知x＞0，y＞0，x+2y=1，若不等式 $\frac{2}{x} + \frac{1}{y}$ ＞m²+2m成立，则实数m的取值范围是（）

A、m≥4或m≤﹣2 B、m≥2或m≤﹣4 C、﹣2＜m＜4 D、﹣4＜m＜2

查看试题解析
17. 在△ABC中，已知AB=2，AC=3，∠BAC= $\frac{π}{3}$ ， $\vec{B M}$ = $\vec{M C}$ ， $\vec{A E}$ = $\vec{E M}$ ， $\vec{B E} \cdot \vec{C E}$ =（）

A、 $- \frac{9}{16}$ B、 $\frac{9}{16}$ C、 $- \frac{7}{16}$ D、 $\frac{7}{16}$

查看试题解析
18. 若存在x∈R，使不等式|x﹣1|+|x﹣a|≤a²﹣a成立，则实数a的取值范围（）

A、a≥1 B、a≤﹣1 C、a≤﹣1或a≥1 D、﹣1≤a≤1

查看试题解析

二、填空题

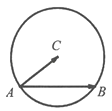
19. 设向量 $\vec{a}$ =（2，1）， $\vec{b}$ =（3，2），则| $\vec{a} + \vec{b}$ |= ．

查看试题解析
20. 角A为△ABC的一个内角，且sinA+cosA= $\frac{1}{3}$ ，则cos2A值为．

查看试题解析
21. 如图，定圆C半径为2，A为圆C上的一个定点，B为圆C上的动点，若点A，B，C不共线，且| $\vec{A B} - t \vec{A C}$ | $\geq | \vec{B C}$ |对任意t∈（0，+∞）恒成立，则 $\vec{A B} \cdot \vec{A C}$ = ．

查看试题解析
22. 已知a，b∈R，若a²+b²﹣ab=1，则ab的取值范围是．

查看试题解析

三、解答题

23. 设函数f（x）=﹣ $\frac{\sqrt{3}}{2}$ sinx $- \frac{1}{2}$ cosx+1

(1)、求函数f（x）的最小正周期和单调递增区间；
（Ⅱ）若x∈[0， $\frac{π}{2}$ ]，且f（x）= $\frac{1}{3}$ ，求cosx的值．

查看试题解析
24. 在△ABC中，已知AB=2，cosB= $\frac{1}{3}$
（Ⅰ）若AC=2 $\sqrt{2}$ ，求sinC的值；
（Ⅱ）若点D在边AC上，且AD=2DC，BD= $\frac{4}{3} \sqrt{3}$ ，求BC的长．

查看试题解析
25. 已知数列{a_n]的前n项和记为S_n ，且满足S_n=2a_n﹣n，n∈N*
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）证明： $\frac{n}{2} - \frac{1}{3} < \frac{a_{1}}{a_{2}} + \frac{a_{2}}{a_{3}}$ +… $+ \frac{a_{n}}{a_{n + 1}} < \frac{n}{2}$ （n∈N*）

查看试题解析