浙江省杭州市2016-2017学年高一下学期期末数学考试试卷

试卷更新日期：2017-09-14 类型：期末考试

进入出卷网下载

一、选择题

1. 设集合A={1，2，3}，B={2，4，6}，则A∩B=（）

A、2 B、{2} C、{2，3，4} D、{1，2，3，4，6}

查看试题解析
2. 设点A（0，1），B（3，2），则 $\vec{A B}$ =（）

A、（﹣1，4） B、（1，3） C、（3，1） D、（7，4）

查看试题解析
3. 函数f（x）=log₂（x+2）的定义域是（）

A、[2，+∞） B、[﹣2，+∞） C、（﹣2，+∞） D、（﹣∞，﹣2）

查看试题解析
4. 函数y=a^x^﹣1（a＞0，a≠1）的图象经过点（）

A、（ $\frac{1}{4}$ ，1） B、（0，1） C、（1，1） D、（ $\frac{1}{2}$ ，1）

查看试题解析
5. 设 $\vec{e_{1}}$ ， $\vec{e_{2}}$ 是平面 $\vec{α}$ 的一组基底，则能作为平面 $\vec{α}$ 的一组基底的是（）

A、 $\vec{e_{1}}$ ﹣ $\vec{e_{2}}$ ， $\vec{e_{2}}$ ﹣ $\vec{e_{1}}$ B、 $\vec{e_{2}}$ +2 $\vec{e_{1}}$ ， $\vec{e_{1}}$ + $\frac{1}{2} \vec{e_{2}}$ C、2 $\vec{e_{2}}$ ﹣3 $\vec{e_{1}}$ ，6 $\vec{e_{1}}$ ﹣4 $\vec{e_{2}}$ D、 $\vec{e_{1}}$ + $\vec{e_{2}}$ ， $\vec{e_{1}}$ ﹣ $\vec{e_{2}}$

查看试题解析
6. 若a²⁰¹⁷=b（a＞0，且a≠1），则（）

A、log_ab=2017 B、log_ba=2017 C、log₂₀₁₇a=b D、log₂₀₁₇b=a

查看试题解析
7. 在△ABC中，若a=2，b=2 $\sqrt{3}$ ，A=30°，则B等于（）

A、30° B、30°或150° C、60° D、60°或 120°

查看试题解析
8. 下列函数中，不满足f（3x）=3f（x）的是（）

A、f（x）=|x| B、f（x）=﹣x C、f（x）=x﹣|x| D、f（x）=x+3

查看试题解析
9. 在△ABC中，角A、B、C所对应的边分别为a，b，c，若 $\frac{c}{b}$ ＜cosA，则△ABC为（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、非钝角三角形

查看试题解析
10. 设函数f（x）=ax²+bx+c（a，b，c∈R）．若f（0）=f（3）＜f（1），则（）

A、a＞0，3a+b=0 B、a＜0，3a+b=0 C、a＞0，9a+b=0 D、a＜0，9a+b=0

查看试题解析
11. 若sin（ $\frac{π}{8}$ +α）= $\frac{3}{4}$ ，则cos（ $\frac{3 π}{8}$ ﹣α）=（）

A、﹣ $\frac{3}{4}$ B、 $\frac{3}{4}$ C、﹣ $\frac{\sqrt{7}}{4}$ D、 $\frac{\sqrt{7}}{4}$

查看试题解析
12. 如图，正方形ABP₇P₅的边长为2，P₁ ， P₄ ， P₆ ， P₂是四边的中点，AB是正方形的其中一条边，P₁P₆与P₂P₄相交于点P₃ ，则 $\vec{A B}$ • $\vec{A P_{i}}$ （i=1，2，…，7）的不同值的个数为（）

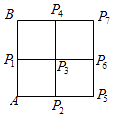A、7 B、5 C、3 D、1

查看试题解析
13. 函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的图象如图所示，为了得到g（x）=Acosωx的图象，可以将f（x）的图象（）

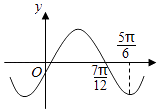A、向左平移 $\frac{π}{12}$ 个单位长度 B、向左平移 $\frac{π}{3}$ 个单位长度 C、向右平移 $\frac{π}{6}$ 个单位长度 D、向右平移 $\frac{5 π}{12}$ 个单位长度

查看试题解析
14. 设O为△ABC的外心，若 $\vec{O A}$ + $\vec{O B}$ + $\vec{O C}$ = $\vec{O M}$ ，则M是△ABC的（）

A、重心（三条中线交点） B、内心（三条角平分线交点） C、垂心（三条高线交点） D、外心（三边中垂线交点）

查看试题解析
15. 若x∈（0， $\frac{π}{2}$ ），则（）

A、x²cos²x＞1 B、 $\frac{x^{4}}{s i n^{2} x}$ ＞ $\frac{3}{4}$ C、x²+cos²x＞1 D、x⁴﹣sin²x＞ $\frac{3}{4}$

查看试题解析

二、填空题

16. 某简谐运动的函数表达式为y=3cos（ $\frac{1}{2}$ t+ $\frac{π}{5}$ ），则该运动的最小正周期为，振幅为，初相为．

查看试题解析
17. 2log₅10+log₅0.25= ．

查看试题解析
18. △ABC中，若 $\vec{A D}$ =2 $\vec{D B}$ ， $\vec{C D}$ = $\frac{1}{3} \vec{C A}$ +λ $\vec{C B}$ ，则λ= ．

查看试题解析
19. 设函数f（x）是奇函数，当x＜0时，f（x）=3^x+x，则当x＞0时，f（x）= ．

查看试题解析
20. 已知sin（α﹣ $\frac{π}{4}$ ）= $\frac{3}{5}$ ，则sin2α= ．

查看试题解析
21. 在△ABC中，内角A、B、C的对边分别为a，b，c，若b=2，cosB= $\frac{1}{4}$ ，sinC=2sinA，则α= ， △ABC的面积S= ．

查看试题解析
22. 已知定义域为正整数集的函数f（x）= ${\begin{matrix} \frac{1}{2} x ， x 为偶数 \\ x - 1 ， x 为奇数 \end{matrix}$ ，f₁（x）=f（x），f_n（x）=f[f_n_﹣1（x）]．若f_n（21）=1，则n=；若f₄（x）=1，则x所有的值构成的集合为．

查看试题解析
23. 在△ABC中，P在△ABC的三边上，MN是△ABC外接圆的直径，若AB=2，BC=3，AC=4，则 $\vec{P M}$ • $\vec{P N}$ 的取值范围是．

查看试题解析

三、解答题

24. 设向量 $\vec{m}$ =（sinx，﹣1）， $\vec{n}$ =（ $\sqrt{3}$ cosx，﹣ $\frac{1}{2}$ ），函数f（x）=（ $\vec{m}$ + $\vec{n}$ ）• $\vec{m}$ ．

(1)、求函数f（x）的单调递增区间；

(2)、当x∈（0， $\frac{π}{2}$ ）时，求函数f（x）的值域．

查看试题解析
25. 设a∈R，函数f（x）=|x²﹣2ax|，方程f（x）=ax+a的四个实数解满足x₁＜x₂＜x₃＜x₄ ．

(1)、求a的取值范围；

(2)、证明：f（x₄）＞ $\frac{76}{3}$ +8 $\sqrt{10}$ ．

查看试题解析