江苏省扬州市2016-2017学年高一下学期期末数学考试试卷

试卷更新日期：2017-09-14 类型：期末考试

进入出卷网下载

一、填空题

1. 计算：cos²15°﹣sin²15°= ．

查看试题解析
2. 不等式x²﹣2x﹣3＜0的解集是．

查看试题解析
3. △ABC中，AB=3，BC=4，B=60°，则AC= ．

查看试题解析
4. 已知圆锥的母线长为5，侧面积为20π，则此圆锥的体积为．

查看试题解析
5. 已知x∈（﹣ $\frac{π}{2}$ ，0），cosx= $\frac{3}{5}$ ，则tan2x= ．

查看试题解析
6. 设变量x，y满足约束条件 ${\begin{matrix} x + y \geq 2 \\ x - y \leq 1 \\ y \leq 2 \end{matrix}$ 则目标函数z=﹣2x+y的最小值为．

查看试题解析
7. 若等差数列{a_n}的前n项和为S_n ， a₂=3，a₃+a₅=﹣2，则使得S_n取最大值时的正整数n= ．

查看试题解析
8. 已知α，β，γ是三个平面，m，n是两条直线，有下列四个命题：
①如果m⊥α，m⊂β，那么α⊥β；
②如果m⊥n，m⊥α，那么n∥α；
③如果α⊥β，m∥α，那么m⊥β；
④如果α∥β，α∩γ=m，β∩γ=n，那么m∥n．
其中正确的命题有．（写出所有正确命题的序号）

查看试题解析
9. 已知0≤θ≤ $\frac{π}{2}$ 且sin（θ﹣ $\frac{π}{6}$ ）= $\frac{1}{3}$ ，则cosθ= ．

查看试题解析
10. 若数列{ $\frac{1}{n (n + 1)}$ }的前n项和为S_n ，若S_n•S_n+1= $\frac{3}{4}$ ，则正整数n的值为．

查看试题解析
11. 已知正数a，b满足 $\frac{1}{a}$ + $\frac{4}{b}$ = $\sqrt{a b}$ ，则ab的最小值为．

查看试题解析
12. 如图，为测量山高MN，选择A和另一座山的山顶C为测量观测点．从A点测得∠NAM=60°，∠CAB=45°以及∠MAC=75°；从C点测得∠MCA=60°；已知山高BC=300米，则山高MN=米．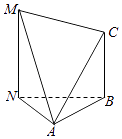

查看试题解析
13. 在数列{a_n}中，a₁+2a₂++2²a₃+…2ⁿ^﹣1a_n=（n•2ⁿ﹣2ⁿ+1）t对任意n∈N^*成立，其中常数t＞0．若关于n的不等式 $\frac{1}{a_{2}}$ + $\frac{1}{a_{4}}$ + $\frac{1}{a_{8}}$ +…+ $\frac{1}{a_{2^{n}}}$ ＞ $\frac{m}{a_{1}}$ 的解集为{n|n≥4，n∈N^*}，则实数m的取值范围是．

查看试题解析
14. 在△ABC中，角A，B，C的对边分别为a，b，c，若a²+b²+4 $\sqrt{2}$ =c² ， ab=4，则 $\frac{s i n C}{t a n^{2} A \cdot s i n 2 B}$ 的最小值是．

查看试题解析

二、解答题：

15. 已知：sin（α+ $\frac{π}{4}$ ）+2sin（α﹣ $\frac{π}{4}$ ）=0．

(1)、求tanα的值；

(2)、若tan（ $\frac{π}{4}$ ﹣β）= $\frac{1}{3}$ ，求tan（α+β）的值．

查看试题解析
16. 已知：三棱锥A﹣BCD中，平面ABD⊥平面BCD，AB⊥AD，E，F分别为BD，AD的中点．

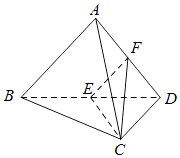(1)、求证：EF∥平面ABC；

(2)、若CB=CD，求证：AD⊥平面CEF．

查看试题解析
17. 已知正项等比数列{a_n}的前n项和为S_n ，且a₂a₃=a₅ ， S₄=10S₂ ．

(1)、求数列{a_n}的通项公式；

(2)、设b_n=（2n﹣1）a_n ，求数列{b_n}的前n项和T_n ．

查看试题解析
18. 在锐角△ABC中，角A，B，C的对边分别为a，b，c，满足 $\frac{2 b - c}{a}$ = $\frac{c o s C}{c o s A}$ ．

(1)、求角A的大小；

(2)、若a= $\sqrt{13}$ ，△ABC的面积S_△ABC=3 $\sqrt{3}$ ，求b+c的值，；

(3)、若函数f（x）=2sinxcos（x+ $\frac{π}{6}$ ），求f（B）的取值范围．

查看试题解析
19. 水培植物需要一种植物专用营养液．已知每投放a（1≤a≤4且a∈R）个单位的营养液，它在水中释放的浓度y（克/升）随着时间x（天）变化的函数关系式近似为y=af（x），其中f（x）= ${\begin{matrix} \frac{4 + x}{4 - x} (0 \leq x \leq 2) \\ 5 - x (2 < x \leq 5) \end{matrix}$ ，若多次投放，则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和，根据经验，当水中营养液的浓度不低于4（克/升）时，它才能有效．

(1)、若只投放一次4个单位的营养液，则有效时间可能达几天？

(2)、若先投放2个单位的营养液，3天后投放b个单位的营养液．要使接下来的2天中，营养液能够持续有效，试求b的最小值．

查看试题解析
20. 已知数列{a_n}满足：对于任意n∈N*且n≥2时，a_n+λa_n_﹣1=2n+1，a₁=4．

(1)、若 $λ = - \frac{1}{3}$ ，求证：{a_n﹣3n}为等比数列；

(2)、若λ=﹣1．①求数列{a_n}的通项公式；
②是否存在k∈N*，使得 $\sqrt{a_{2 k} a_{2 k + 1}}$ +25为数列{a_n}中的项？若存在，求出所有满足条件的k的值；若不存在，请说明理由．

查看试题解析