江苏省淮安市2016-2017学年高一下学期期末数学考试试卷
试卷更新日期：2017-09-14 类型：期末考试
一、填空题
-
1. 2sin15°cos15°= ．2. 一组数据1，3，2，5，4的方差是 ．3. 若x∈（0，1）则x（1﹣x）的最大值为 ．4. 如图是一个算法的流程图，则输出的a的值是 ．
5. 两根相距6m的木杆上系一根绳子，并在绳子上挂一盏灯，则灯与两端距离都大于2m的概率是 ．6. 已知实数x，y满足 ，则目标函数z=x﹣y的最小值为 ．7. 在△ABC中，∠A，∠B，∠C所对的边分别是a，b，c，如果a：b：c=2：3：4，那么cosC= ．8. 若tanα=﹣2，tan（α+β）= ，则tanβ的值是 ．9. 已知{an}是等差数列，Sn是其前n项和，若2a7﹣a5﹣3=0，则S17的值是 ．10. 已知△ABC中，AB= ，BC=1，A=30°，则AC= ．11. 在数列{an}中，a1=2，an+1=2an ， Sn为{an}的前n项和．若sn=254，则n= ．12. 已知{an}是等差数列，a1=1公差d≠0，Sn为其前n项的和，若a1 ， a2 ， a5成等比数列，S10= ．13. 在锐角△ABC中，sinA=sinBsinC，则tanB+2tanC的最小值是 ．14. 已知△ABC中，内角A，B，C的对边分别为a，b，c，若a，b，c成等比数列，则 的取值范围为 ．二、解答题
-
15. 已知sinα= ．(1)、求 的值；(2)、求 的值．16. 已知等差数列{an}中，其前n项和为Sn ， a2=4，S5=30．(1)、求{an}的首项a1和公差d的值；(2)、设数列{bn}满足bn= ，求数列{bn}的前项和Tn ．17. 某学校为了解学校食堂的服务情况，随机调查了50名就餐的教师和学生．根据这50名师生对餐厅服务质量进行评分，绘制出了频率分布直方图（如图所示），其中样本数据分组为[40，50），[50，60），…，[90，100]．
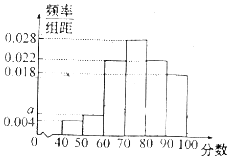(1)、求频率分布直方图中a的值；(2)、从评分在[40，60）的师生中，随机抽取2人，求此人中恰好有1人评分在[40，50）上的概率；(3)、学校规定：师生对食堂服务质量的评分不得低于75分，否则将进行内部整顿，试用组中数据估计该校师生对食堂服务质量评分的平均分，并据此回答食堂是否需要进行内部整顿．18. 已知函数f（x）=ax2+（a﹣2）x﹣2，a∈R．(1)、若关于x的不等式f（x）≤0的解集为[﹣1，2]，求实数a的值；(2)、当a＜0时，解关于x的不等式f（x）≤0．19. 如图，GH是东西方向的公路北侧的边缘线，某公司准备在GH上的一点B的正北方向的A处建设一仓库，设AB=ykm，并在公路北侧建造边长为xkm的正方形无顶中转站CDEF（其中EF在GH上），现从仓库A向GH和中转站分别修两条道路AB，AC，已知AB=AC+1，且∠ABC=60°。
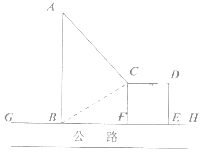(1)、求y关于x的函数解析式，并求出定义域；(2)、如果中转站四堵围墙造价为10万元/km，两条道路造价为30万元/km，问：x取何值时，该公司建设中转站围墙和两条道路总造价M最低．20. 已知数列{an}的前n项和为Sn ， 且满足Sn=n2﹣4n，数列{bn}中，b1= 对任意正整数 ．(1)、求数列{an}的通项公式；(2)、是否存在实数μ，使得数列{3n•bn+μ}是等比数列？若存在，请求出实数μ及公比q的值，若不存在，请说明理由；(3)、求证： ．