2015年湖北省随州市数学中考真题试卷

试卷更新日期：2016-04-22 类型：中考真卷

进入出卷网下载

一、单选题：本大题共10小题，每小题3分，共30分随州市2015年初中毕业升学考试数学试题

1. 在﹣1，﹣2，0，1四个数中最小的数是（　　）

A、﹣1 B、-2 C、0 D、-1

查看试题解析
2.
如图，AB∥CD，∠A=50°，则∠1的大小是（　　）

A、50° B、120° C、130° D、150°

查看试题解析
3. 用配方法解一元二次方程 $x^{2} - 6 x - 4 = 0$ ，下列变形正确的是（　　）

A、 $(x - 6)^{2} = - 4 + 36$ B、 $(x - 6)^{2} = 4 + 36$ C、 $(x - 3)^{2} = - 4 + 9$ D、 $(x - 3)^{2} = 4 + 9$

查看试题解析
4. 下列说法正确的是（　　）

A、“购买1张彩票就中奖”是不可能事件 B、“掷一次骰子，向上一面的点数是6”是随机事件 C、了解我国青年人喜欢的电视节目应作全面调查 D、甲、乙两组数据，若S_甲²＞S_乙² ，则乙组数据波动大

查看试题解析
5.
如图，△ABC中，AB=5，AC=6，BC=4，边AB的垂直平分线交AC于点D，则△BDC的周长是（　　）

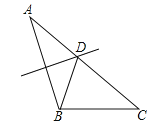A、8 B、9 C、10 D、11

查看试题解析
6. 若代数式 $\frac{1}{1 - x}$ + $\sqrt{x}$ 有意义，则实数x的取值范围是（　　）

A、x≠1 B、x≥0 C、x≠0 D、x≥0且x≠1

查看试题解析
7.
如图，在△ABC中，点D、E分别在边AB、AC上，下列条件中不能判断△ABC∽△AED的是（　　）

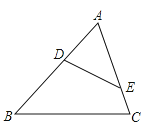A、∠AED=∠B B、∠ADE=∠C C、 $\frac{A D}{A E}$ = $\frac{A C}{A B}$ D、 $\frac{A D}{A B}$ = $\frac{A E}{A C}$

查看试题解析
8.
如图，⊙O是正五边形ABCDE的外接圆，这个正五边形的边长为a，半径为R，边心距为r，则下列关系式错误的是（　　）

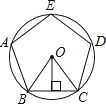A、 $R^{2} - r^{2} = a^{2}$ B、 $a = 2 R \sin 36 °$ C、 $a = 2 r \tan 36 °$ D、 $r = R \cos 36 °$

查看试题解析
9. 在直角坐标系中，将点（﹣2，3）关于原点的对称点向左平移2个单位长度得到的点的坐标是（　　）

A、（4，﹣3） B、（﹣4，3） C、（0，﹣3） D、（0，3）

查看试题解析
10.
甲骑摩托车从A地去B地，乙开汽车从B地去A地，同时出发，匀速行驶，各自到达终点后停止，设甲、乙两人间距离为s（单位：千米），甲行驶的时间为t（单位：小时），s与t之间的函数关系如图所示，有下列结论：
①出发1小时时，甲、乙在途中相遇；
②出发1.5小时时，乙比甲多行驶了60千米；
③出发3小时时，甲、乙同时到达终点；
④甲的速度是乙速度的一半．
其中，正确结论的个数是（　　）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题：本大题共6小题，每小题3分，共18分

11. 4的算术平方根是，9的平方根是，﹣27的立方根是．

查看试题解析
12. 为创建“全国环保模范城”，我市对白云湖73个排污口进行了封堵，每年可减少污水排放185000吨，将185000用科学记数法表示为．

查看试题解析
13.
如图是一个长方体的三视图（单位：cm），根据图中数据计算这个长方体的体积是 cm³ ．

查看试题解析
14. 某校抽样调查了七年级学生每天体育锻炼时间，整理数据后制成了如下所示的频数分布表，这个样本的中位数在第组．
组别
时间（小时）
频数（人）
第1组
0≤t＜0.5
12
第2组
0.5≤t＜1
24
第3组
1≤t＜1.5
18
第4组
1.5≤t＜2
10
第5组
2≤t＜2.5
6

查看试题解析
15.
观察下列图形规律：当n= 时，图形“●”的个数和“△”的个数相等．

查看试题解析
16. 在▱ABCD中，AB＜BC，已知∠B=30°，AB= $2 \sqrt{3}$ ，将△ABC沿AC翻折至△AB′C，使点B′落在▱ABCD所在的平面内，连接B′D．若△AB′D是直角三角形，则BC的长为．

查看试题解析

三、解答题：本大题共9小题，共72分

17.
解不等式组请结合题意，完成本题解答．

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、
把不等式①和②的解集在数轴上表示出来：
；

(4)、原不等式组的解集为．

查看试题解析
18. 先化简，再求值：（2+a）（2﹣a）+a（a﹣5b）+3a⁵b³÷（﹣a²b）² ，其中ab=﹣ $\frac{1}{2}$ ．

查看试题解析
19. 端午节前夕，小东的父母准备购买若干个粽子和咸鸭蛋（每个粽子的价格相同，每个咸鸭蛋的价格相同）．已知粽子的价格比咸鸭蛋的价格贵1.8元，花30元购买粽子的个数与花12元购买咸鸭蛋的个数相同，求粽子与咸鸭蛋的价格各多少？

查看试题解析
20.
如图，反比例函数y= $\frac{k}{x}$ （k＜0）的图象与矩形ABCD的边相交于E、F两点，且BE=2AE，E（﹣1，2）．

(1)、求反比例函数的解析式；

(2)、连接EF，求△BEF的面积．

查看试题解析
21.
为推进“传统文化进校园”活动，某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组．学生报名情况如图（每人只能选择一个小组）：

(1)、报名参加课外活动小组的学生共有人，将条形图补充完整；

(2)、扇形图中m= ，n= ；

(3)、根据报名情况，学校决定从报名“经典诵读”小组的甲、乙、丙、丁四人中随机安排两人到“地方戏曲”小组，甲、乙恰好都被安排到“地方戏曲”小组的概率是多少？请用列表或画树状图的方法说明．

查看试题解析
22.
如图，射线PA切⊙O于点A，连接PO．

(1)、在PO的上方作射线PC，使∠OPC=∠OPA（用尺规在原图中作，保留痕迹，不写作法），并证明：PC是⊙O的切线；

(2)、
在（1）的条件下，若PC切⊙O于点B，AB=AP=4，求的长．

查看试题解析
23.
如图，某足球运动员站在点O处练习射门，将足球从离地面0.5m的A处正对球门踢出（点A在y轴上），足球的飞行高度y（单位：m）与飞行时间t（单位：s）之间满足函数关系y=at²+5t+c，已知足球飞行0.8s时，离地面的高度为3.5m．

(1)、足球飞行的时间是多少时，足球离地面最高？最大高度是多少？

(2)、若足球飞行的水平距离x（单位：m）与飞行时间t（单位：s）之间具有函数关系x=10t，已知球门的高度为2.44m，如果该运动员正对球门射门时，离球门的水平距离为28m，他能否将球直接射入球门？

查看试题解析
24.
问题：如图（1），点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系．

(1)、【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG，从而发现EF=BE+FD，请你利用图（1）证明上述结论．

(2)、【类比引申】
如图（2），四边形ABCD中，∠BAD≠90°，AB=AD，∠B+∠D=180°，点E、F分别在边BC、CD上，则当∠EAF与∠BAD满足系时，仍有EF=BE+FD．

(3)、【探究应用】
如图（3），在某公园的同一水平面上，四条通道围成四边形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，且AE⊥AD，DF=40（ $\sqrt{3}$ ﹣1）米，现要在E、F之间修一条笔直道路，求这条道路EF的长（结果取整数，参考数据： $\sqrt{2}$ =1.41， $\sqrt{3}$ =1.73）

查看试题解析
25.
如图，已知抛物线y= $\frac{\sqrt{2}}{8}$ （x+2）（x﹣4）与x轴交于点A、B（点A位于点B的左侧），与y轴交于点C，CD∥x轴交抛物线于点D，M为抛物线的顶点．

(1)、求点A、B、C的坐标；

(2)、设动点N（﹣2，n），求使MN+BN的值最小时n的值；

(3)、P是抛物线上一点，请你探究：是否存在点P，使以P、A、B为顶点的三角形与△ABD相似（△PAB与△ABD不重合）？若存在，求出点P的坐标；若不存在，说明理由．

查看试题解析

组别	时间（小时）	频数（人）
第1组	0≤t＜0.5	12
第2组	0.5≤t＜1	24
第3组	1≤t＜1.5	18
第4组	1.5≤t＜2	10
第5组	2≤t＜2.5	6