2015年湖北省荆门市数学中考真题试卷
试卷更新日期:2016-04-22 类型:中考真卷
一、选择题(本题共12小题,每小题3分,共36分,每小题给出的四个选项,有且只有一个答案是正确的)
-
1. 64的立方根是( )A、4 B、 C、8 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下面四个几何体中,俯视图为四边形的是( )A、
 B、
B、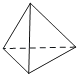 C、
C、 D、
D、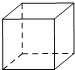 4. 某市2014年的国民生产总值为2073亿元,这个数用科学记数法表示为( )A、元 B、元 C、元 D、元5. 已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为( )A、8或10 B、8 C、10 D、6或126.
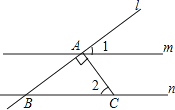
4. 某市2014年的国民生产总值为2073亿元,这个数用科学记数法表示为( )A、元 B、元 C、元 D、元5. 已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为( )A、8或10 B、8 C、10 D、6或126.如图,m∥n,直线l分别交m,n于点A,点B,AC⊥AB,AC交直线n于点C,若∠1=35°,则∠2等于( )
 A、35° B、45° C、55° D、65°7. 若关于x的一元二次方程x2﹣4x+5﹣a=0有实数根,则a的取值范围是( )A、a≥1 B、a>1 C、a≤1 D、a<18. 当1<a<2时,代数式的值是( )A、-1 B、1 C、2a-3 D、3-2a9.
A、35° B、45° C、55° D、65°7. 若关于x的一元二次方程x2﹣4x+5﹣a=0有实数根,则a的取值范围是( )A、a≥1 B、a>1 C、a≤1 D、a<18. 当1<a<2时,代数式的值是( )A、-1 B、1 C、2a-3 D、3-2a9.在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )
 A、甲的速度随时间的增加而增大 B、乙的平均速度比甲的平均速度大 C、在起跑后第180秒时,两人相遇 D、在起跑后第50秒时,乙在甲的前面10. 在排球训练中,甲、乙、丙三人相互传球,由甲开始发球(记作为第一次传球),则经过三次传球后,球仍回到甲手中的概率是( )A、 B、 C、 D、11.
A、甲的速度随时间的增加而增大 B、乙的平均速度比甲的平均速度大 C、在起跑后第180秒时,两人相遇 D、在起跑后第50秒时,乙在甲的前面10. 在排球训练中,甲、乙、丙三人相互传球,由甲开始发球(记作为第一次传球),则经过三次传球后,球仍回到甲手中的概率是( )A、 B、 C、 D、11.如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为( )
 A、 B、 C、 D、12.
A、 B、 C、 D、12.如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(本题共5小题,每小题3分,共15分)
-
13. 不等式组的解集是 .
14. 王大爷用280元买了甲、乙两种药材,甲种药材每千克20元,乙种药材每千克60元,且甲种药材比乙种药材多买了2千克,则甲种药材买了 千克.15. 已知关于x的一元二次方程x2+(m+3)x+m+1=0的两个实数根为x1 , x2 , 若x12+x22=4,则m的值为 .16.在矩形ABCD中,AB=5,AD=12,将矩形ABCD沿直线l向右翻滚两次至如图所示位置,则点B所经过的路线长是 (结果不取近似值).
 17.
17.如图,点A1 , A2依次在y=(x>0)的图象上,点B1 , B2依次在x轴的正半轴上.若△A1OB1 , △A2B1B2均为等边三角形,则点B2的坐标为 .

三、解答题(本题共7小题,共69分)
-
18. 先化简,再求值:•﹣ , 其中a=1+ , b=1﹣ .19.
已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.
求证:四边形ABCD为菱形.
 20.
20.为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如图所示的统计图表.
组别
身高(cm)
A
x<150
B
150≤x<155
C
155≤x<160
D
160≤x<165
E
x≥165

根据图表中信息,回答下列问题:
(1)、在样本中,男生身高的中位数落在 (填组别序号),女生身高在B组的人数有 ;(2)、在样本中,身高在150≤x<155之间的人数共有 ,身高人数最多的在 (填组别序号);(3)、已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生约有多少人?21.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
 22.
22.已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
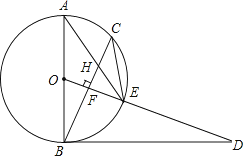 (1)、求证:BD是⊙O的切线;(2)、求证:CE2=EH•EA;(3)、若⊙O的半径为5,sinA= , 求BH的长。
(1)、求证:BD是⊙O的切线;(2)、求证:CE2=EH•EA;(3)、若⊙O的半径为5,sinA= , 求BH的长。
23. 甲经销商库存有1200套A品牌服装,每套进价400元,每套售价500元,一年内可卖完,现市场流行B品牌服装,每套进价300元,每套售价600元,但一年内只允许经销商一次性订购B品牌服装,一年内B品牌服装销售无积压,因甲经销商无流动资金可用,只有低价转让A品牌服装,用转让来的资金购进B品牌服装,并销售,经与乙经销商协商,甲、乙双方达成转让协议,转让价格y(元/套)与转让数量x(套)之间的函数关系式为y=﹣x+360(100≤x≤1200),若甲经销商转让x套A品牌服装,一年内所获总利润为W(元).(1)、求转让后剩余的A品牌服装的销售款Q1(元)与x(套)之间的函数关系式;(2)、求B品牌服装的销售款Q2(元)与x(套)之间的函数关系式;(3)、求W(元)与x(套)之间的函数关系式,并求W的最大值.24.如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
 (1)、求OE的长及经过O,D,C三点抛物线的解析式;(2)、一动点P从点C出发,沿CB以每秒2个单位长度的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长度的速度向点C运动,当点P到达点B时,两点同时停止运动,设运动时间为t秒,当t为何值时,DP=DQ;(3)、若点N在(1)中抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点坐标;若不存在,请说明理由.
(1)、求OE的长及经过O,D,C三点抛物线的解析式;(2)、一动点P从点C出发,沿CB以每秒2个单位长度的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长度的速度向点C运动,当点P到达点B时,两点同时停止运动,设运动时间为t秒,当t为何值时,DP=DQ;(3)、若点N在(1)中抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点坐标;若不存在,请说明理由.