2015年湖北省黄石市数学中考真题试卷

试卷更新日期：2016-04-22 类型：中考真卷

进入出卷网下载

一、单选题（每小题3分，共30分每小题的四个选项中只有一个是正确的）

1. ﹣5的倒数是（　　）

A、5 B、 $\frac{1}{5}$ C、-5 D、 $- \frac{1}{5}$

查看试题解析
2. 国家统计局数据显示，截至2014年末全国商品房待售面积约为62200万平方米，62200万用科学记数法可表示为（　　）

A、 $6.22 \times 10^{4}$ B、 $6.22 \times 10^{7}$ C、 $6.22 \times 10^{8}$ D、 $6.22 \times 10^{9}$

查看试题解析
3. 下列运算正确的是（　　）

A、4m﹣m=3 B、 $2 m^{2} \cdot m^{3} = 2 m^{5}$ C、 $(- m^{3})^{2} = m^{9}$ D、﹣（m+2n）=﹣m+2n

查看试题解析
4.
下列四个立体图形中，左视图为矩形的是（　　）

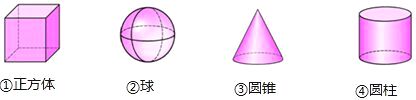A、①③ B、①④ C、②③ D、③④

查看试题解析
5. 某班组织了一次读书活动，统计了10名同学在一周内的读书时间，他们一周内的读书时间累计如表，则这10名同学一周内累计读书时间的中位数是（　　）
一周内累计的读书时间（小时）
5
8
10
14
人数（个）
1
4
3
2

A、8 B、7 C、9 D、10

查看试题解析
6. 在下列艺术字中既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
7.
在长方形ABCD中AB=16，如图所示裁出一扇形ABE，将扇形围成一个圆锥（AB和AE重合），则此圆锥的底面半径为（　　）

A、4 B、16 C、 $4 \sqrt{2}$ D、8

查看试题解析
8.
如图，在等腰△ABC中，AB=AC，BD⊥AC，∠ABC=72°，则∠ABD=（　　）

A、36° B、54° C、18° D、64°

查看试题解析
9. 当1≤x≤2时，ax+2＞0，则a的取值范围是（　　）

A、a＞﹣1 B、a＞﹣2 C、a＞0 D、a＞﹣1且a≠0

查看试题解析
10.
如图是自行车骑行训练场地的一部分，半圆O的直径AB=100，在半圆弧上有一运动员C从B点沿半圆周匀速运动到M（最高点），此时由于自行车故障原地停留了一段时间，修理好继续以相同的速度运动到A点停止．设运动时间为t，点B到直线OC的距离为d，则下列图象能大致刻画d与t之间的关系是（　　）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 分解因式：3x²﹣27= ．

查看试题解析
12. 反比例函数y= $\frac{2 a - 1}{x}$ 的图象有一支位于第一象限，则常数a的取值范围是．

查看试题解析
13.
九年级（3）班共有50名同学，如图是该班一次体育模拟测试成绩的频数分布直方图（满分为30分，成绩均为整数）．若将不低于23分的成绩评为合格，则该班此次成绩达到合格的同学占全班人数的百分比是．

查看试题解析
14.
如图，圆O的直径AB=8，AC=3CB，过C作AB的垂线交圆O于M，N两点，连结MB，则∠MBA的余弦值为．

查看试题解析
15. 一食堂需要购买盒子存放食物，盒子有A，B两种型号，单个盒子的容量和价格如表．现有15升食物需要存放且要求每个盒子要装满，由于A型号盒子正做促销活动：购买三个及三个以上可一次性返还现金4元，则购买盒子所需要最少费用为元．
型号
A
B
单个盒子容量（升）
2
3
单价（元）
5
6

查看试题解析
16.
现有多个全等直角三角形，先取三个拼成如图1所示的形状，R为DE的中点，BR分别交AC，CD于P，Q，易得BP：QR：QR=3：1：2．
（1）若取四个直角三角形拼成如图2所示的形状，S为EF的中点，BS分别交AC，CD，DE于P，Q，R，则BP：PQ：QR：RS= ；
（2）若取五个直角三角形拼成如图3所示的形状，T为FG的中点，BT分别交AC，CD，DE，EF于P，Q，R，S，则BP：PQ：QR：RS：ST= ．

查看试题解析

三、解答题

17. 计算：﹣ $\sqrt{8}$ +|﹣ $\sqrt{2}$ |+2sin45°+π⁰+（ $\frac{1}{2}$ ）^﹣¹ ．

查看试题解析
18. 先化简，再求值： $\frac{x^{2} - 4 x + 4}{x} \div (\frac{2}{x} - 1)$ ，其中x=2﹣ $\sqrt{2}$ ．

查看试题解析
19.
如图，⊙O的直径AB=4，∠ABC=30°，BC交⊙O于D，D是BC的中点．

(1)、求BC的长；

(2)、过点D作DE⊥AC，垂足为E，求证：直线DE是⊙O的切线．

查看试题解析
20. 解方程组 $\{\begin{matrix} x^{2} + 4 y^{2} = 4 \\ \sqrt{3} x + 2 y = 2 \end{matrix}$ ．

查看试题解析

四、综合题

21. 父亲节快到了，明明准备为爸爸煮四个大汤圆作早点：一个芝麻馅，一个水果馅，两个花生馅，四个汤圆除内部馅料不同外，其它一切均相同．

(1)、求爸爸吃前两个汤圆刚好都是花生馅的概率；

(2)、若给爸爸再增加一个花生馅的汤圆，则爸爸吃前两个汤圆都是花生馅的可能性是否会增大？请说明理由．

查看试题解析
22.
如图所示，体育场内一看台与地面所成夹角为30°，看台最低点A到最高点B的距离为10 $\sqrt{3}$ ， A，B两点正前方有垂直于地面的旗杆DE．在A，B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°（仰角即视线与水平线的夹角）

(1)、求AE的长；

(2)、已知旗杆上有一面旗在离地1米的F点处，这面旗以0.5米/秒的速度匀速上升，求这面旗到达旗杆顶端需要多少秒？

查看试题解析
23. 大学毕业生小王响应国家“自主创业”的号召，利用银行小额无息贷款开办了一家饰品店．该店购进一种今年新上市的饰品进行销售，饰品的进价为每件40元，售价为每件60元，每月可卖出300件．市场调查反映：调整价格时，售价每涨1元每月要少卖10件；售价每下降1元每月要多卖20件．为了获得更大的利润，现将饰品售价调整为60+x（元/件）（x＞0即售价上涨，x＜0即售价下降），每月饰品销量为y（件），月利润为w（元）．

(1)、直接写出y与x之间的函数关系式；

(2)、如何确定销售价格才能使月利润最大？求最大月利润；

(3)、为了使每月利润不少于6000元应如何控制销售价格？

查看试题解析
24.
在△AOB中，C，D分别是OA，OB边上的点，将△OCD绕点O顺时针旋转到△OC′D′．

(1)、如图1，若∠AOB=90°，OA=OB，C，D分别为OA，OB的中点，证明：①AC′=BD′；②AC′⊥BD′；

(2)、如图2，若△AOB为任意三角形且∠AOB=θ，CD∥AB，AC′与BD′交于点E，猜想∠AEB=θ是否成立？请说明理由．

查看试题解析
25. 已知双曲线y= $\frac{1}{x}$ （x＞0），直线l₁：y﹣ $\sqrt{2}$ =k（x﹣ $\sqrt{2}$ ）（k＜0）过定点F且与双曲线交于A，B两点，设A（x₁ ， y₁），B（x₂ ， y₂）（x₁＜x₂），直线l₂：y=﹣x+ $\sqrt{2}$ ．

(1)、若k=﹣1，求△OAB的面积S；

(2)、若AB= $\frac{5}{2} \sqrt{2}$ ，求k的值；

(3)、设N（0，2 $\sqrt{2}$ ），P在双曲线上，M在直线l₂上且PM∥x轴，求PM+PN最小值，并求PM+PN取得最小值时P的坐标．
（参考公式：在平面直角坐标系中，若A（x₁ ， y₁），B（x₂ ， y₂）则A，B两点间的距离为AB= $\sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}}$ ）

查看试题解析

一周内累计的读书时间（小时）	5	8	10	14
人数（个）	1	4	3	2

型号	A	B
单个盒子容量（升）	2	3
单价（元）	5	6