2015年黑龙江省绥化市中考数学真题试卷

试卷更新日期：2016-04-22 类型：中考真卷

进入出卷网下载

一、单选题

1.
下列图案中，既是中心对称又是轴对称图形的个数有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2.
如图是一些完全相同的小正方体搭成的几何体的三视图．这个几何体只能是（　　）

A、 B、 C、 D、

查看试题解析
3. 从长度分别为1、3、5、7的四条线段中任选三条作边，能构成三角形的概率为（　　）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
4. 石墨烯是现在世界上最薄的纳米材料，其理论厚度仅是0.00000000034m，这个数用科学记数法表示正确的是（　　）

A、 $3.4 \times 10^{- 9}$ B、 $0.34 \times 10^{- 9}$ C、 $3.4 \times 10^{- 10}$ D、^{$3.4 \times 10^{- 11}$}

查看试题解析
5. 将一副三角尺按如图方式进行摆放，∠1、∠2不一定互补的是（　　）

A、 B、 C、 D、

查看试题解析
6. 在实数0、π、 $\frac{22}{7}$ 、 $\sqrt{2}$ 、﹣ $\sqrt{9}$ 中，无理数的个数有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7.
如图，反比例函数y= $\frac{k}{x}$ （x＜0）的图象经过点P，则k的值为（　　）

A、﹣6 B、-5 C、6 D、5

查看试题解析
8. 关于x的不等式组 $\{\begin{matrix} x > a \\ x > 1 \end{matrix}$ 的解集为x＞1，则a的取值范围是（　　）

A、 $a > 1$ B、 $a < 1$ C、 $a \geq 1$ D、 $a \leq 1$

查看试题解析
9.
如图，在矩形ABCD中，AB=10，BC=5．若点M、N分别是线段AC，AB上的两个动点，则BM+MN的最小值为（　　）

A、10 B、8 C、 $5 \sqrt{3}$ D、6

查看试题解析
10.
如图，▱ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB= $\frac{1}{2}$ BC，连接OE．下列结论：①∠CAD=30°；②S_▱ABCD=AB•AC；③OB=AB；④OE= $\frac{1}{4}$ BC，成立的个数有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每题3分，满分33分）

11. 计算：| $\sqrt{3} - 4$ |﹣ ${(\frac{1}{2})}^{- 2}$ = .

查看试题解析
12. 在函数y= $\frac{1}{\sqrt{x + 2}}$ +（x﹣2）⁰中，自变量x的取值范围是 .

查看试题解析
13. 点A（﹣3，2）关于x轴的对称点A′的坐标为 .

查看试题解析
14. 若代数式 $\frac{x^{2} - 5 x + 6}{2 x - 6}$ 的值等于0，则x= .

查看试题解析
15. 若关于x的一元二次方程ax²+2x﹣1=0无解，则a的取值范围是 .

查看试题解析
16. 把二次函数y=2x²的图象向左平移1个单位长度，再向下平移2个单位长度，平移后抛物线的解析式为 .

查看试题解析
17.
在2015年的体育考试中某校6名学生的体育成绩统计如图所示，这组数据的中位数是 .

查看试题解析
18.
如图，正方形ABCD的对角线相交于点O，△OEF是正三角形，且AE=BF，则∠AOE= .

查看试题解析
19.
如图，将一块含30°角的直角三角板和半圆量角器按如图的方式摆放，使斜边与半圆相切．若半径OA=2，则图中阴影部分的面积为．（结果保留π）

查看试题解析
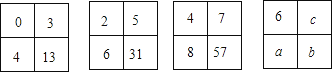
20.
填在下面各正方形中的四个数之间都有一定的规律，按此规律得出a+b+c= .

查看试题解析
21. 在矩形ABCD中，AB=4，BC=3，点P在AB上．若将△DAP沿DP折叠，使点A落在矩形对角线上的A′处，则AP的长为 .

查看试题解析

三、解答题（满分57分）

22. 先化简，再求值：（ $\frac{x + 2}{x^{2} - 2 x}$ ﹣ $\frac{x - 1}{x^{2} - 4 x + 4}$ ）÷ $\frac{x - 4}{x}$ ，其中x=tan60°+2．

查看试题解析
23. 在平面直角坐标系xOy中，直线y=﹣x+3与x轴、y轴分别交于A、B，在△AOB内部作正方形，使正方形的四个顶点都落在该三角形的边上，求正方形落在x轴正半轴的顶点坐标．

查看试题解析
24.
如图，以线段AB为直径作⊙O，CD与⊙O相切于点E，交AB的延长线于点D，连接BE，过点O作OC∥BE交切线DE于点C，连接AC．

(1)、求证：AC是⊙O的切线；

(2)、若BD=OB=4，求弦AE的长．

查看试题解析
25. 现有甲、乙两个容器，分别装有进水管和出水管，两容器的进出水速度不变，先打开乙容器的进水管，2分钟时再打开甲容器的进水管，又过2分钟关闭甲容器的进水管，再过4分钟同时打开甲容器的进、出水管．直到12分钟时，同时关闭两容器的进出水管．打开和关闭水管的时间忽略不计．容器中的水量y（升）与乙容器注水时间x（分）之间的关系如图所示．

(1)、求甲容器的进、出水速度．

(2)、甲容器进、出水管都关闭后，是否存在两容器的水量相等？若存在，求出此时的时间．

(3)、若使两容器第12分钟时水量相等，则乙容器6分钟后进水速度应变为多少？

查看试题解析
26. 自学下面材料后，解答问题．
分母中含有未知数的不等式叫分式不等式．如： $\frac{x - 2}{x + 1} > 0 ； \frac{2 x + 3}{x - 1} < 0$ 等．那么如何求出它们的解集呢？
根据我们学过的有理数除法法则可知：两数相除，同号得正，异号得负．其字母表达式为：
（1）若a＞0，b＞0，则 $\frac{a}{b}$ ＞0；若a＜0，b＜0，则 $\frac{a}{b}$ ＞0；
（2）若a＞0，b＜0，则 $\frac{a}{b}$ ＜0；若a＜0，b＞0，则 $\frac{a}{b}$ ＜0．
反之：（1）若 $\frac{a}{b}$ ＞0，则 $\{\begin{matrix} a > 0 \\ b > 0 \end{matrix}$ 或 $\{\begin{matrix} a < 0 \\ b < 0 \end{matrix}$
（2） $\frac{a}{b}$ ＜0，则____________　．
根据上述规律，求不等式 $\frac{x - 2}{x + 1}$ ＞0的解集．

查看试题解析
27. 某苹果生产基地，用30名工人进行采摘或加工苹果，每名工人只能做其中一项工作．苹果的销售方式有两种：一种是可以直接出售；另一种是可以将采摘的苹果加工成罐头出售．直接出售每吨获利4000元；加工成罐头出售每吨获利10000元．采摘的工人每人可以采摘苹果0.4吨；加工罐头的工人每人可加工0.3吨．设有x名工人进行苹果采摘，全部售出后，总利润为y元．

(1)、求y与x的函数关系式．

(2)、如何分配工人才能获利最大？

查看试题解析
28.
如图1，在正方形ABCD中，延长BC至M，使BM=DN，连接MN交BD延长线于点E．

(1)、求证：BD+2DE= $\sqrt{2}$ BM．

(2)、如图2，连接BN交AD于点F，连接MF交BD于点G．若AF：FD=1：2，且CM=2，则线段DG=_____；

查看试题解析
29.
如图，已知抛物线y=ax²+bx+c与x轴交于点A、B，与直线AC：y=﹣x﹣6交y轴于点C，点D是抛物线的顶点，且横坐标为﹣2．

(1)、求出抛物线的解析式．

(2)、判断△ACD的形状，并说明理由．

(3)、直线AD交y轴于点F，在线段AD上是否存在一点P，使∠ADC=∠PCF？若存在，直接写出点P的坐标；若不存在，说明理由．

查看试题解析