广东省深圳市龙岗区2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2020-04-30 类型:期末考试
一、选择题:
-
1. 五个新篮球的质量与标准质量相差(单位:克)分别是+5、﹣3.5、+0.7、﹣2.5、﹣0.6,正数表示超过标准质量的克数,负数表示不足标准质量的克数.最接近标准质量的是( )A、﹣2.5 B、﹣0.6 C、+0.7 D、+52. 如图所示为几何体的平面展开图,则从左到右,其对应的几何体名称分别为( )
 A、圆锥,正方体,三棱锥,圆柱 B、正方体,圆锥,四棱锥,圆柱 C、正方体,圆锥,四棱柱,圆柱 D、正方体,圆锥,圆柱,三棱柱3. 如图,是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该位置小正方体的个数,则这个几何体的主视图(从正面看)是( )
A、圆锥,正方体,三棱锥,圆柱 B、正方体,圆锥,四棱锥,圆柱 C、正方体,圆锥,四棱柱,圆柱 D、正方体,圆锥,圆柱,三棱柱3. 如图,是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该位置小正方体的个数,则这个几何体的主视图(从正面看)是( ) A、
A、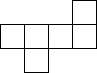 B、
B、 C、
C、 D、
D、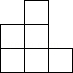 4. 深圳地铁14号线连接福田中心区、布吉、横岗、大运新城、坪山中心、坑梓,支撑整个东部发展轴,覆盖东部地区南北向交通需求走廊。该地铁线全长约50340米,共设站17座,采用自动化无人驾驶,预计2022年竣工,其中50340米用科学记数法表示为( )A、5.034×104 B、5.034×103 C、5.034×105 D、5×1055. 下列说法中不正确的是( )A、﹣ ab2的系数是﹣ B、﹣2ab2的次数是2 C、3a2b与ba2是同类项 D、多项式mn2+2mn﹣3n﹣1的次数是36. 点A、B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论,其中正确的是( )
4. 深圳地铁14号线连接福田中心区、布吉、横岗、大运新城、坪山中心、坑梓,支撑整个东部发展轴,覆盖东部地区南北向交通需求走廊。该地铁线全长约50340米,共设站17座,采用自动化无人驾驶,预计2022年竣工,其中50340米用科学记数法表示为( )A、5.034×104 B、5.034×103 C、5.034×105 D、5×1055. 下列说法中不正确的是( )A、﹣ ab2的系数是﹣ B、﹣2ab2的次数是2 C、3a2b与ba2是同类项 D、多项式mn2+2mn﹣3n﹣1的次数是36. 点A、B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论,其中正确的是( )①b﹣a<0; ②a+b>0; ③|a|<|b|; ④ab>0.
 A、①② B、③④ C、①③ D、②④7. 在下列调查方式中,较为合适的是( )A、为了解深圳市中小学生的视力情况,采用普查的方式 B、为了解龙岗区中小学生的课外阅读习惯情况,采用普查的方式 C、为了解某校七年级(2)班学生期末考试数学成绩情况,采用抽样调查方式 D、为了解我市市民对消防安全知识的了解情况,采用抽样调查的方式8. 钟面上12点30分,时针与分针的夹角是( )A、150o B、165o C、170o D、175o9. 如图,边长为a的正方形中阴影部分的面积为( )
A、①② B、③④ C、①③ D、②④7. 在下列调查方式中,较为合适的是( )A、为了解深圳市中小学生的视力情况,采用普查的方式 B、为了解龙岗区中小学生的课外阅读习惯情况,采用普查的方式 C、为了解某校七年级(2)班学生期末考试数学成绩情况,采用抽样调查方式 D、为了解我市市民对消防安全知识的了解情况,采用抽样调查的方式8. 钟面上12点30分,时针与分针的夹角是( )A、150o B、165o C、170o D、175o9. 如图,边长为a的正方形中阴影部分的面积为( ) A、a2﹣ πa2 B、 πa2 C、a2﹣πa2 D、πa210. 如图,点C在线段AB上,点D是AC的中点,如果CB=2CD,AB=20cm,那么BC的长为( )
A、a2﹣ πa2 B、 πa2 C、a2﹣πa2 D、πa210. 如图,点C在线段AB上,点D是AC的中点,如果CB=2CD,AB=20cm,那么BC的长为( ) A、5cm B、8cm C、10cm D、12cm11. 若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则 的值为( )A、 B、49! C、2450 D、5012. 观察图中正方形四个顶点所标的数字规律,可得出数2018应标在( )
A、5cm B、8cm C、10cm D、12cm11. 若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则 的值为( )A、 B、49! C、2450 D、5012. 观察图中正方形四个顶点所标的数字规律,可得出数2018应标在( ) A、第504个正方形的左下角 B、第504个正方形的右上角 C、第505个正方形的左下角 D、第505个正方形的右下角
A、第504个正方形的左下角 B、第504个正方形的右上角 C、第505个正方形的左下角 D、第505个正方形的右下角二、填空题:
-
13. 下列平面图形中,将编号为(只需填写编号)的平面图形绕轴旋转一周,可得到图中所示的立体图形.
 14. 21.54°用度、分、秒表示为 .15. 作图:已知线段a、b,请用尺规作线段EF使EF=a+b.请将下列作图步骤按正确的顺序排列出来(只填序号).
14. 21.54°用度、分、秒表示为 .15. 作图:已知线段a、b,请用尺规作线段EF使EF=a+b.请将下列作图步骤按正确的顺序排列出来(只填序号).作法:①以M为端点在射线MG上用圆规截取MF=b;②作射线EG;③以E为端点在射线EG上用圆规截取EM=a;④EF即为所求的线段。
16. 《九章算术》是中国古代的数学专著,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数、羊价各几何?”译文:“假设有若干人共同出钱买羊,如果每人出5钱,那么还差45钱;如果每人出7钱那么仍旧差3钱,求买羊的人数和羊的价钱.”设共有x个人买羊,可列方程为 .三、解答题
-
17. 计算:(1)、(2)、18. 先化简,再求值:
,其中a=-2.
19. 解方程(1)、4x-10=6(x-2)(2)、20. 《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从2018年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的统计图,已知“查资料”的人数是40人.
请你根据以上信息解答下列问题:
(1)、在扇形统计图中,“玩游戏”对应的百分比为 , 圆心角度数是度;(2)、补全条形统计图;(3)、该校共有学生2100人,估计每周使用手机时间在2小时以上(不含2小时)的人数.21. 如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°. (1)、若∠AOC=48°,求∠DOE的度数.(请写出求解过程)(2)、若∠AOC=α,则∠DOE=(用含α的代数式表示).22. 某蔬菜经营户,用1200元从菜农手里批发了长豆角和番茄共450千克,长豆角和番茄当天的批发价和零售价如表:
(1)、若∠AOC=48°,求∠DOE的度数.(请写出求解过程)(2)、若∠AOC=α,则∠DOE=(用含α的代数式表示).22. 某蔬菜经营户,用1200元从菜农手里批发了长豆角和番茄共450千克,长豆角和番茄当天的批发价和零售价如表:品名
长豆角
番茄
批发价(元/千克)
3.2
2.4
零售价(元/千克)
5.0
3.6
(1)、这天该经营户批发了长豆角和番茄各多少千克?(2)、当天卖完这些番茄和长豆角能盈利多少元?23. 如图

如图1,点C在线段AB上,图中共有3条线段:AB、AC和BC,若其中有一条线段的长度是另一条线段长度的两倍,则称点C是线段AB的一个“二倍点”.
(1)、一条线段的中点这条线段的“二倍点”;(填“是”或“不是”)(2)、如图2,若线段AB=20cm,点M从点B的位置开始,以每秒2cm的速度向点A运动,当点M到达点A时停止运动,运动的时间为t秒.问t为何值时,点M是线段AB的“二倍点”.
(3)、同时点N从点A的位置开始,以每秒1cm的速度向点B运动,并与点M同时停止.请直接写出点M是线段AN的“二倍点”时t的值.