吉林省2019届普通高中高三理数第三次联合模拟考试试卷
试卷更新日期:2020-04-30 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则集合 子集的个数为( )A、 B、 C、 D、2. 已知 ,复数 , ,且 为实数,则 ( )A、 B、 C、3 D、-33. 新闻出版业不断推进供给侧结构性改革,深入推动优化升级和融合发展,持续提高优质出口产品供给,实现了行业的良性发展.下面是2012年至2016年我国新闻出版业和数字出版业营收增长情况,则下列说法错误的是( )
 A、2012年至2016年我国新闻出版业和数字出版业营收均逐年增加 B、2016年我国数字出版业营收超过2012年我国数字出版业营收的2倍 C、2016年我国新闻出版业营收超过2012年我国新闻出版业营收的1.5倍 D、2016年我国数字出版营收占新闻出版营收的比例未超过三分之一4. 已知等差数列 的前13项和为52,则 ( )A、256 B、-256 C、32 D、-325. 已知双曲线 : 的左、右两个焦点分别为 , ,若存在点 满足 ,则该双曲线的离心率为( )A、2 B、 C、 D、56. 函数 的图象大致是( )A、
A、2012年至2016年我国新闻出版业和数字出版业营收均逐年增加 B、2016年我国数字出版业营收超过2012年我国数字出版业营收的2倍 C、2016年我国新闻出版业营收超过2012年我国新闻出版业营收的1.5倍 D、2016年我国数字出版营收占新闻出版营收的比例未超过三分之一4. 已知等差数列 的前13项和为52,则 ( )A、256 B、-256 C、32 D、-325. 已知双曲线 : 的左、右两个焦点分别为 , ,若存在点 满足 ,则该双曲线的离心率为( )A、2 B、 C、 D、56. 函数 的图象大致是( )A、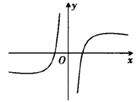 B、
B、 C、
C、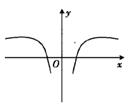 D、
D、 7. 在菱形 中, , , , 分别为 , 的中点,则 ( )A、 B、 C、5 D、8. 已知函数 的图像向右平移 个单位长度后,得到的图像关于 轴对称, ,当 取得最小值时,函数 的解析式为( )A、 B、 C、 D、9. 若某几何体的三视图如图所示,则该几何体的表面积为( )
7. 在菱形 中, , , , 分别为 , 的中点,则 ( )A、 B、 C、5 D、8. 已知函数 的图像向右平移 个单位长度后,得到的图像关于 轴对称, ,当 取得最小值时,函数 的解析式为( )A、 B、 C、 D、9. 若某几何体的三视图如图所示,则该几何体的表面积为( ) A、240 B、264 C、274 D、28210. 已知数列 是公比为 的等比数列,且 ,若数列 是递增数列,则 的取值范围为( )A、 B、 C、 D、11. 已知抛物线 : 的焦点为 ,过点 的直线 交抛物线 于 , 两点,其中点 在第一象限,若弦 的长为 ,则 ( )A、2或 B、3或 C、4或 D、5或12. 已知函数 , ,若对 , 且 ,使得 ,则实数 的取值范围是( )A、 B、 C、 D、
A、240 B、264 C、274 D、28210. 已知数列 是公比为 的等比数列,且 ,若数列 是递增数列,则 的取值范围为( )A、 B、 C、 D、11. 已知抛物线 : 的焦点为 ,过点 的直线 交抛物线 于 , 两点,其中点 在第一象限,若弦 的长为 ,则 ( )A、2或 B、3或 C、4或 D、5或12. 已知函数 , ,若对 , 且 ,使得 ,则实数 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 在区间 内任意取一个数 ,则 恰好为非负数的概率是.14. 已知实数 , 满足 ,则目标函数 的最小值为 .15. 某高校开展安全教育活动,安排6名老师到4个班进行讲解,要求1班和2班各安排一名老师,其余两个班各安排两名老师,其中刘老师和王老师不在一起,则不同的安排方案有种.16. 在四面体 中, 与 都是边长为2的等边三角形,且平面 平面 ,则该四面体外接球的体积为 .
三、解答题
-
17. 在 中,角 所对的边分别是 ,且 .(1)、求角 的大小;(2)、若 ,求边长 .18. 如图,在三棱柱 中, 是边长为2的等边三角形, , , .
 (1)、证明:平面 平面 ;(2)、 , 分别是 , 的中点, 是线段 上的动点,若二面角 的平面角的大小为 ,试确定点 的位置.19. 一年之计在于春,一日之计在于晨,春天是播种的季节,是希望的开端.某种植户对一块地的 个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为 ,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.(1)、当 取何值时,有3个坑要补播种的概率最大?最大概率为多少?(2)、当 时,用 表示要补播种的坑的个数,求 的分布列与数学期望.20. 已知△ABC的两个顶点A , B的坐标分别为( ,0),( ,0),圆E是△ABC的内切圆,在边AC , BC , AB上的切点分别为P , Q , R , |CP|=2 ,动点C的轨迹为曲线G.(1)、求曲线G的方程;(2)、设直线l与曲线G交于M , N两点,点D在曲线G上, 是坐标原点 ,判断四边形OMDN的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
(1)、证明:平面 平面 ;(2)、 , 分别是 , 的中点, 是线段 上的动点,若二面角 的平面角的大小为 ,试确定点 的位置.19. 一年之计在于春,一日之计在于晨,春天是播种的季节,是希望的开端.某种植户对一块地的 个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为 ,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.(1)、当 取何值时,有3个坑要补播种的概率最大?最大概率为多少?(2)、当 时,用 表示要补播种的坑的个数,求 的分布列与数学期望.20. 已知△ABC的两个顶点A , B的坐标分别为( ,0),( ,0),圆E是△ABC的内切圆,在边AC , BC , AB上的切点分别为P , Q , R , |CP|=2 ,动点C的轨迹为曲线G.(1)、求曲线G的方程;(2)、设直线l与曲线G交于M , N两点,点D在曲线G上, 是坐标原点 ,判断四边形OMDN的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.