江苏省镇江市句容市2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2020-04-30 类型:期中考试
一、单选题
-
1. 下列各组图形可以通过平移互相得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 下列图形中,由AB∥CD,能得到∠1=∠2的是A、
2. 下列计算正确的是( )A、 B、 C、 D、3. 下列图形中,由AB∥CD,能得到∠1=∠2的是A、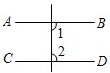 B、
B、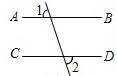 C、
C、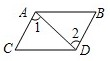 D、
D、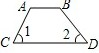 4. 若x2+kxy+16y2是一个完全平方式,那么k的值为( )A、4 B、8 C、±8 D、±165. 下列变形,属于因式分解的有( )
4. 若x2+kxy+16y2是一个完全平方式,那么k的值为( )A、4 B、8 C、±8 D、±165. 下列变形,属于因式分解的有( )①x2﹣16=(x+4)(x﹣4)②x2+3x﹣16=x(x+3)﹣16
③(x+4)(x﹣4)=x2﹣16 ④x2+x=x(x+1)
A、1个 B、2个 C、3个 D、4个6. 一个凸n边形,其每个内角都是140°,则n的值为( )A、6 B、7 C、8 D、97. 若a=﹣0.32 , b=﹣3﹣2 , c= ,d= ,则( )A、a<b<c<d B、b<a<d<c C、a<d<c<b D、c<a<d<b8. 已知a=2019x+2018,b=2019x+2019,c=2019x+2020.则多项式a2+b2+c2﹣ab﹣bc﹣ac的值为( )A、1 B、2 C、3 D、4二、填空题
-
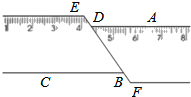
9. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,用科学记数法表示是克.10. 计算:m2•m3=11. 因式分解:x2﹣4= .12. 如图,一把直尺沿直线断开并错位,点E、D、B、F在同一直线上,若∠ADE=145°,则∠DBC的度数为 .
 13. 如图,将一副三角板的两个直角重合,使点B在EC上,点D在AC上,已知∠A=45°,∠E=30°,则∠BFD的度数是 .
13. 如图,将一副三角板的两个直角重合,使点B在EC上,点D在AC上,已知∠A=45°,∠E=30°,则∠BFD的度数是 . 14. 若关于x的多项式x2﹣mx+n能因式分解为:(x﹣2)(x+3),则m+n=15. 已知 ,则 .16. 若5m=3,5n=2,则5m﹣2n的值为 .17. × = .18. 若m2+n2﹣2m+4n+5=0.则m﹣n= .19. 四边形ABCD中,∠A=100°,∠C=70°.点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN.若MF∥AD,FN∥DC,则∠D=°.
14. 若关于x的多项式x2﹣mx+n能因式分解为:(x﹣2)(x+3),则m+n=15. 已知 ,则 .16. 若5m=3,5n=2,则5m﹣2n的值为 .17. × = .18. 若m2+n2﹣2m+4n+5=0.则m﹣n= .19. 四边形ABCD中,∠A=100°,∠C=70°.点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN.若MF∥AD,FN∥DC,则∠D=°. 20. 如图,△ABC中,点E是BC上的一点,BC=3BE,点D是AC的中点,若S△ADF﹣S△BEF=2.则S△ABC= .
20. 如图,△ABC中,点E是BC上的一点,BC=3BE,点D是AC的中点,若S△ADF﹣S△BEF=2.则S△ABC= .
三、解答题
-
21. 计算(1)、(2)、2a3(a2)3÷a(3)、(x﹣1)2﹣x(x+1)(4)、20002﹣1999×2001(用简便方法计算)22. 因式分解(1)、3x2﹣27(2)、3m2n﹣12mn+12n(3)、m2(m﹣n)+n2(n﹣m)(4)、x4﹣8x2y2+16y423. 先化简,再求值:4(x﹣1)2﹣(2x+3)(2x﹣3),其中x=﹣1.24. 如图,在每个小正方形边长为1的方格纸中,△ADC的顶点都在方格纸格点上,将△ABC向左平移1格.再向上平移1格,

①在图中画出平移后的△A′B′C′;
②画出AB边上的高CE;
③过点A画BC的平行线;
④在图中,若△BCQ的面积等于△BCA的面积.则图中满足条件且异于点A的个点Q共有_▲_个.(注:格点指网格线的交点)
25. 如图,已知四边形ABCD中,∠D=∠B=90°,AE平分∠DAB,CF平分∠DCB (1)、若∠DAB=72°,∠2=°,∠3=°;(2)、求证:AE∥CF.26. 一天,小明和小红玩纸片拼图游戏.发现利用图①中的三种材料各若干可以拼出一些图形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2 .
(1)、若∠DAB=72°,∠2=°,∠3=°;(2)、求证:AE∥CF.26. 一天,小明和小红玩纸片拼图游戏.发现利用图①中的三种材料各若干可以拼出一些图形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2 . (1)、图③可以解释为等式: .(2)、图④中阴影部分的面积为 . 观察图④请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .(3)、如图⑤,小明利用7个长为b,宽为a的长方形拼成如图所示的大长方形;
(1)、图③可以解释为等式: .(2)、图④中阴影部分的面积为 . 观察图④请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .(3)、如图⑤,小明利用7个长为b,宽为a的长方形拼成如图所示的大长方形;①若AB=4,若长方形AGMB的面积与长方形EDHN的面积的差为S,试计算S的值(用含a,b的代数式表示)
②若AB为任意值,且①中的S的值为定值,求a与b的关系.
27.
(1)、如图1所示,△ABC中,∠ACB的角平分线CF与∠EAC的角平分线AD的反向延长线交于点F;
①若∠B=90°则∠F=▲;
②若∠B=a,求∠F的度数(用a表示);
(2)、如图2所示,若点G是CB延长线上任意一动点,连接AG,∠AGB与∠GAB的角平分线交于点H,随着点G的运动,∠F+∠H的值是否变化?若变化,请说明理由;若不变,请求出其值.