江苏省无锡市江阴市澄东片2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2020-04-30 类型：期中考试

进入 出卷网 下载

一、单选题

  • 1. 如图所示的图案可以看作由“基本图案”经过平移得到的是（　　）
    A、 B、 C、 D、

    查看试题解析

  • 2. 下列计算正确的是（    ）
    A、a2•a3=a6 B、a6÷a3=a2 C、（a2）3=a6 D、（2a）3=6a3

    查看试题解析

  • 3. 如果a＝（－99）0 ，b＝（－0.1）-1 ， c＝（－ 53 ）-2 ， 那么a、b．c三数的大小关系为（   ）
    A、a>c>b B、c>a>b C、a>b>c D、c>b>a

    查看试题解析

  • 4. 下列式子不能因式分解的是（ ）
    A、x2-1    B、2x2+x    C、－x2－9    D、x2-4x+4

    查看试题解析

  • 5. 已知a∥b，一块含30°角的直角三角板如图所示放置，∠2=45°，则∠1等于（   ）

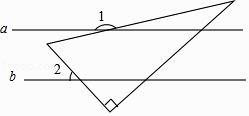    A、100° B、135° C、155° D、165°

    查看试题解析

  • 6. 如图，在△ACB中，∠ACB=90°，∠A=24°，D是AB上一点．将△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′的度数为（      ）

    A、42° B、40° C、30° D、24°

    查看试题解析

  • 7. 如图，要得到AB∥CD，只需要添加一个条件，这个条件不可以是（      ）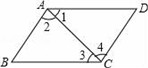

    A、∠1＝∠3 B、∠B＋∠BCD＝180° C、∠2＝∠4 D、∠D＋∠BAD＝180°

    查看试题解析

  • 8. 若（2x+3y）（mx-ny）=9y2-4x2 ， 则m、n的值为（     ）
    A、m=2，n=3 B、m=-2，n=-3 C、m=2，n=-3 D、m=-2，n=3

    查看试题解析

  • 9. 如图，把一个三角形纸片ABC的三个顶角向内折叠之后（3个顶点不重合），那么图中 ∠1+∠2+∠3+∠4+∠5+∠6 的度数和是（   ）

    A、180° B、270° C、360° D、540°

    查看试题解析

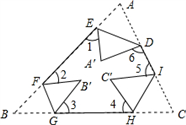  • 10. 3（22+1）（24+1）…（232+1）+1计算结果的个位数字是（　　）
    A、4 B、6 C、2 D、8

    查看试题解析

二、填空题

  • 11. 习总书记提出“生态兴则文明兴”、“守住绿水青山，就是守住金山银山”，人人都有爱护环境的义务．某时刻在无锡监测点监测到PM 2.5的含量为65微克/米3 ， 即0.000065克/米3 ， 将0.000065用科学记数法表示为 ．

    查看试题解析

  • 12. 已知一个多边形的每一个内角都是 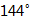，则这个多边形是边形.

    查看试题解析

  • 13. 如果三角形的两边长分别是3和5，那么它的第三边x的取值范围是.

    查看试题解析

  • 14. 代数式x2-（k-1）x+25是一个完全平方式，则k=.

    查看试题解析

  • 15. 计算（-8）2018×（-0.125）2019的结果是

    查看试题解析

  • 16. 已知a，b，c是三角形的三边长，化简：|a-b+c|-|a-b-c|=.

    查看试题解析

  • 17. 如图，已知∠1＝70°，∠C+∠D+∠E+∠F+∠A+∠B＝.

    查看试题解析

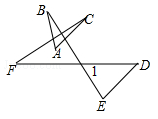  • 18. 如图，线段AB，AC是两条绕点A可以自由旋转的线段（但点A，B，C始终不在同一条直线上），已知AB=5，AC=7，点D，E分别是AB，BC的中点，则四边形BEFD面积的最大值是.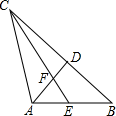

    查看试题解析

三、解答题

  • 19. 计算：
    (1)、(−13)−1−(−3)2+(π−2)0 ；
    (2)、（-2a3）2•3a3+6a12÷（-2a3）；
    (3)、（x+1）（x-2）-（x-2）2；
    (4)、（a+2b+3）（a+2b-3）

    查看试题解析

  • 20. 把下面各式分解因式：
    (1)、8a3b2-12ab3c
    (2)、4m2-16n2
    (3)、（x2+2x）2+2（x2+2x）+1

    查看试题解析

  • 21. 如图，∠1=80°，∠2=100°∠C=∠D.

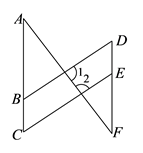    (1)、判断AC与DF的位置关系，并说明理由；
    (2)、若∠C比∠A大20°，求∠F的度数.

    查看试题解析

  • 22. 如图：在正方形网格中有一个△ABC，按要求进行下列作图（只能借助于网格）：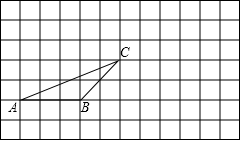

    ①画出△ABC中BC边上的高AD；

    ②画出先将△ABC向右平移6格，再向上平移3格后的△A1B1C1；

    ③若格点△PAB与格点△PBC的面积相等，则这样的点P共_▲_个.

    查看试题解析

  • 23.   
    (1)、已知m＋4n-3=0，求2m·16n的值．
    (2)、已知n为正整数，且x2n＝4，求（x3n）2－2（x2）2n的值．

    查看试题解析

  • 24. 甲同学在拼图探索活动中发现，用4个形状大小完全相同的直角三角形（直角边长分别为a，b，斜边长为c），可以拼成像如图1那样的正方形，并由此得出了关于a2 ， b2 ， c2的一个等式.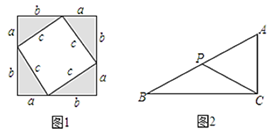

    (1)、请你写出这一结论：▲ ， 并给出验证过程.
    (2)、试用上述结论解决问题：如图2，P是Rt△ABC斜边AB上的一个动点，已知AC=5，AB=13，求PC的最小值.

    查看试题解析

  • 25. 如图，△ABC中，∠C=90°，AC=12，BC=9，AB=15，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒3个单位，设运动的时间为t秒.

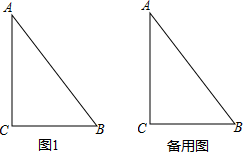    (1)、当t=时，CP把△ABC的面积分成相等的两部分；
    (2)、当t=5时，CP把△ABC分成的两部分面积之比是S△APC：S△BPC=
    (3)、当t=时，△BPC的面积为18.

    查看试题解析

  • 26. 初一（7）班数学学习小组“孙康映雪”在学习了第七章平面图形的认识（二）后对几何学习产生了浓厚的兴趣．请你认真研读下列三个片段，并完成相关问题．如图1，直线OM⊥ON，垂足为O，三角板的直角顶点C落在∠MON的内部，三角板的另两条直角边分别与ON、OM交于点D和点B．

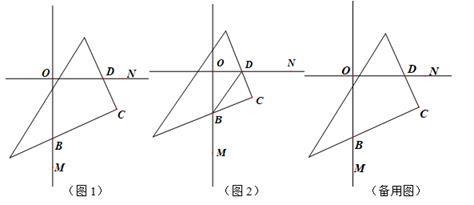    (1)、小孙说：由四边形内角和知识很容易得到∠OBC+∠ODC的值．如果你是小孙，得到的正确答案应是：∠OBC+∠ODC=°．
    (2)、小康说：连结BD（如图2），若BD平分∠OBC，那么BD也平分∠ODC．请你说明当BD平分∠OBC时，BD也平分∠ODC的理由．
    (3)、小雪说：若DE平分∠ODC、BF平分∠MBC，我发现DE与BF具有特殊的位置关系．请你先在备用图中补全图形，再判断DE与BF有怎样的位置关系并说明理由．

    查看试题解析