江苏省苏州市吴江区2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2020-04-30 类型：期中考试

进入出卷网下载

一、单选题

1. ${(- \frac{2}{3})}^{5} \times {(\frac{3}{2})}^{4}$ 等于（）

A、1 B、 $- \frac{2}{3}$ C、 $- 1$ D、 $\frac{2}{3}$

查看试题解析
2. 把多项式 $2 x^{2} - 8$ 分解因式，结果正确的是（）

A、 $2 (x^{2} - 8)$ B、 $2 {(x - 2)}^{2}$ C、 D、 $2 x (x - \frac{4}{x})$

查看试题解析
3. PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物。2.5微米等于0.0000025米，把0.0000025用科学记数法表示为（）

A、0.25×10^–5米 B、2.5×10^–7米 C、2.5×10^–6米 D、25×10^–7米

查看试题解析
4. 如图，已知直线a、b被直线c所截，则① $∠ 1 = ∠ 2$ ；② $∠ 1 = ∠ 3$ ；③ $∠ 2 = ∠ 3$ ；④ $∠ 3 + ∠ 4 = 180 °$ 中，正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 以下四种沿 $A B$ 折叠的方法中，由相应条件不一定能判定纸带两条边线a、b互相平行的是（）

A、展开后测得 $∠ 1 = ∠ 2$ B、展开后测得 $∠ 1 = ∠ 2$ 且 $∠ 3 = ∠ 4$ C、测得 $∠ 1 = ∠ 2$ D、测得 $∠ 1 = ∠ 2$

查看试题解析
6. 一个多边形的每个内角都相等，并且它的一个外角与一个内角的比为1:3，则这个多边形为（）

A、三角形 B、四边形 C、六边形 D、八边形

查看试题解析
7. 下列等式由左边到右边的变形中，属于因式分解的是（）

A、 $6 a b = 2 a \cdot 3 b$ B、 $x^{2} - 4 + 3 x = (x + 2) (x - 2) + 3 x$ C、 $x^{2} - 9 = (x + 3) (x - 3)$ D、 $(x + 2) (x - 2) = x^{2} - 4$

查看试题解析
8. 若 $a = {(- \frac{1}{3})}^{- 2}$ ， $b = - {0.3}^{2}$ ， $c = - 3^{- 2}$ ， $d = {(- \frac{1}{3})}^{0}$ ，则它们的大小关系是（）

A、a<b<c<d B、b<c<d<a C、a<d<c<b D、c<b<d<a

查看试题解析
9. 如图，直线 $A B / / C D$ ，点 $E$ 在 $C D$ 上，点 $O$ 、点 $F$ 在 $A B$ 上， $∠ E O F$ 的角平分线 $O G$ 交 $C D$ 于点 $G$ ，过点 $F$ 作 $F H ⊥ O E$ 于点 $H$ ，已知 $∠ O G D = 148 °$ ，则 $∠ O F H$ 的度数为（）

A、26º B、32º C、36º D、42º

查看试题解析
10. 下列结论中，错误结论有（）；①三角形三条高（或高的延长线）的交点不在三角形的内部，就在三角形的外部；②一个多边形的边数每增加一条，这个多边形的内角和就增加360º；③两条平行直线被第三条直线所截，同旁内角的角平分线互相平行；④三角形的一个外角等于任意两个内角的和；⑤在 $Δ A B C$ 中，若 $∠ A = \frac{1}{2} ∠ B = \frac{1}{3} ∠ C$ ，则 $Δ A B C$ 为直角三角形；⑥顺次延长三角形的三边，所得的三角形三个外角中锐角最多有一个

A、6个 B、5个 C、4个 D、3个

查看试题解析

二、填空题

11. 如图是婴儿车的平面示意图，其中 $A B / / C D$ ， $∠ 1 = 120 °$ ， $∠ 3 = 40 °$ ，那么 $∠ 2$ 的度数为.

查看试题解析
12. 若 $x^{2} + 2 a x + 36$ 是完全平方式，则 $a =$ .

查看试题解析
13. 计算：若 $a + b = 4$ ， $a - b = 1$ ，则 ${(a + 1)}^{2} - {(b - 1)}^{2}$ 的值为.

查看试题解析
14. $Δ A B C$ 中， $A B = 10$ ， $B C = 2 x$ ， $A C = 3 x$ ，则 $x$ 的取值范围是.

查看试题解析
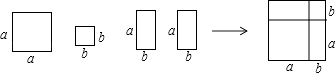
15.
利用1个a×a的正方形，1个b×b的正方形和2个a×b的矩形可拼成一个正方形（如图所示），从而可得到因式分解的公式．

查看试题解析
16. 4个数a、b、c、d排列成 $| \begin{matrix} a & b \\ c & d \end{matrix} |$ ，我们称之二阶行列式，规定它的运算法则为 $| \begin{matrix} a & b \\ c & d \end{matrix} | = a d - b c$ ，若 $| \begin{matrix} x - 2 & x + 3 \\ x + 1 & x - 2 \end{matrix} | = 7$ ，则 $x =$

查看试题解析
17. 已知 $a = \frac{1}{2019} + 2018$ ， $b = \frac{1}{2019} + 2019$ ， $c = \frac{1}{2019} + 2020$ ，则代数式 $2 (a^{2} + b^{2} + c^{2} - a b - b c - a c)$ 的值是.

查看试题解析

三、解答题

18. 计算：

(1)、 $- {(- 1)}^{- 3} + 2019^{2} - 2017 \times 2021$

(2)、 $- 2 x y \cdot 3 x^{2} y - x^{2} y (- 3 x y + x y^{2})$ ；

(3)、 $(2 a - b) (2 b + a) - {(a - 3 b)}^{2}$

查看试题解析
19.

(1)、解不等式，并将解集在数轴上表示出来： $4 - \frac{x - 2}{2} < \frac{x}{3}$ ；

(2)、若不等式组 ${\begin{array}{l} \frac{x}{2} + a \geq 2 \\ 2 x - b < 3 \end{array}$ 的解集是 $0 \leq x < 1$ ，求 $a + b$ 的值.

查看试题解析
20. 先化简，再求值： $(2 x + 3) (2 x - 3) - x (5 x + 4) - {(x - 1)}^{2}$ ，其中 $x^{2} + x - 2019 = 0$ .

查看试题解析
21. 分解因式：

(1)、 $a x^{2} - 6 a x + 9 a$ ；

(2)、 $(m + 1) (m - 9) + 8 m$ ；

(3)、 $a^{4} + 3 a^{2} - 4$

查看试题解析
22. 如图，直线 $A B$ 、 $C D$ 相交于点 $O$ . $∠ A O D = 2 ∠ B O D + 60 °$ .

(1)、求 $∠ B O D$ 的度数；

(2)、以 $O$ 为端点引射线 $O E$ 、 $O F$ ，射线 $O E$ 平分 $∠ B O D$ ，且 $∠ E O F = 90 °$ ，求 $∠ B O F$ 的度数.

查看试题解析
23. 已知 $3^{x} = 15$ ， $5^{y} = 15$ ，

(1)、求 $27^{x} \div 5^{y + 2}$ 的值；

(2)、求 $\frac{1}{x} + \frac{1}{y}$ 的值.

查看试题解析
24. 已知 $Δ A B C$ 中，三边长a、b、c，且满足 $a = b + 2$ ， $b = c + 1$ .

(1)、试说明b一定大于3；

(2)、若这个三角形周长为22，求a、b、c.

查看试题解析
25. 已知 $A B / / C D$ .

(1)、如图1， $B P$ 、 $D P$ 分别平分 $∠ A B E$ 、 $∠ E D C$ .试说明： $∠ B P D = \frac{1}{2} ∠ B E D$ ；

(2)、如图2，若 $∠ B M N = 133 °$ ， $∠ M N D = 145 °$ ， $B P$ 、 $D P$ 分别平分 $∠ A B M$ 、 $∠ C D N$ ，那么 $∠ B P D =$ º（只要直接填上正确结论即可）.

查看试题解析
26. 如图1，点 $O$ 为直线 $A B$ 上一点，过点 $O$ 作射线 $O C$ ，使 $∠ A O C = 120 °$ ，将一把直角三角尺的直角顶点放在点 $O$ 处，一边 $O M$ 在射线 $O A$ 上，另一边 $O N$ 在直线 $A B$ 的下方，其中 $∠ O M N = 30 °$ .

(1)、将图1中的三角尺绕点 $O$ 顺时针旋转至图2，使一边 $O M$ 在 $∠ A O C$ 的内部，且恰好平分 $∠ A O C$ ，求 $∠ C O N$ 的度数；

(2)、将图1中三角尺绕点 $O$ 按每秒10º的速度沿顺时针方向旋转一周，旋转过程中，在第秒时，边 $M N$ 恰好与射线 $O C$ 平行；在第秒时，直线 $O N$ 恰好平分锐角 $∠ B O C$ .

(3)、将图1中的三角尺绕点 $O$ 顺时针旋转至图3，使 $O N$ 在 $∠ B O C$ 的内部，请探究 $∠ B O M$ 与 $∠ N O C$ 之间的数量关系，并说明理由.

查看试题解析