江苏省南京市鼓楼区2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2020-04-30 类型：期中考试

进入出卷网下载

一、单选题

1. 计算（a²）³ ，结果正确的是（　　）

A、 $a^{6}$ B、 $a^{5}$ C、 $2 a^{3}$ D、 $a^{9}$

查看试题解析
2. 下列多项式中能用平方差公式分解因式的是（　　）

A、 $x^{2} + 4^{}$ B、 $x^{2} - x y^{}$ C、 $x^{2} - 9^{}$ D、 $- x^{2} - y^{2}$

查看试题解析
3. 如图，点E在BC的延长线上，下列条件中能判断AB∥CD的是（　　）

A、 $∠ 3 = ∠ 4$ B、 $∠ 1 = ∠ 2$ C、 $∠ B = ∠ 2$ D、 $∠ D = ∠ D C E$

查看试题解析
4. 下列命题是真命题的是（　　）

A、相等的角是对顶角 B、若 $x^{2} = y^{2}$ ，则 $x = y$ C、同角的余角相等 D、两直线平行，同旁内角相等

查看试题解析
5. 如图，一个人从A点出发沿北偏东30°方向走到B点，若这个人再从B点沿南偏东15°方向走到C点则∠ABC等于（　　）

A、 $15^{\circ}$ B、 $30^{\circ}$ C、 $45^{\circ}$ D、 $165^{\circ}$

查看试题解析
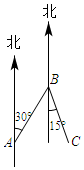6. 若x、y、a满足方程组 ${\begin{cases} x + 2 y = 1 - a \\ x - y = 2 a - 5 \end{cases}$ ，则2^2x•4^y的值为（　　）

A、1 B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析

二、填空题

7. 据报道，我国中芯国际公司突破欧美技术封锁，计划2019年年内量产世界领先水平的14nm芯片，14mm即0.000 000 014m，0.000 000 014用科学记数法表示为．

查看试题解析
8. 命题“同位角相等，两直线平行”的逆命题是：．

查看试题解析
9. （）+2a）²=4a²+4a+1．

查看试题解析
10. 已知a+b=2，a-b=-1，则a²-b²= ．

查看试题解析
11. 如图，将边长为6cm的正方形ABCD先向下平移2cm，再向左平移1cm，得到正方形A'B'C'D'，则这两个正方形重叠部分的面积为cm² ．

查看试题解析
12. 某农户饲养了白鸡、黑鸡共200只，白鸡的只数是黑鸡的三倍，设白鸡有x只，黑鸡有y只，根据题意可列二元一次方程组：．

查看试题解析
13. 计算： ${(\frac{2}{3})}^{2018} \times {(\frac{3}{2})}^{2019} \times {(- 1)}^{6}$ = ．

查看试题解析
14. 如图，直线EF分别交直线AB、CD于点G、H，AB∥CD，MG⊥EF，垂足为G，HN平分∠CHE，∠NHC=32°，则∠AGM= ．

查看试题解析
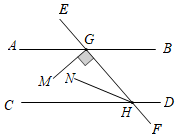15. 我们学过的“幂的运算”有：①同底数幂的乘法，②幂的乘方，③积的乘方，④同底数幂的除法．在“（a⁴•a⁵）²=（a⁴）²•（a⁵）²=a⁸•a¹⁰=a¹⁸”的运算过程中，运用了上述幂的运算中的（按运算顺序填序号）．

查看试题解析
16. 将长为2、宽为a（a大于1且小于2）的长方形纸片按如图①所示的方式折叠并压平，剪下一个边长等于长方形宽的正方形，称为第一次操作：再把剩下的长方形按如图②所示的方式折叠并压平，剪下个边长等于此时长方形宽的正方形，称为第二次操作：如此反复操作下去…，若在第n次操作后，剩下的长方形恰为正方形，则操作终止当n=3时，a的值为．

查看试题解析

三、解答题

17. 先化简，再求值：（x+3）（x-3）-2x（x+3）+（x-1）² ，其中x= $- \frac{1}{2}$

查看试题解析
18. 解二元一次方程组的关键是“消元”，即把“二元”转化为“一元”，同样，我们可以用“消元”的方法解三元一次方程组．下面，我们就来解一个三元一次方程组：
解方程组 ${\begin{array}{l} x + y + z = 2 ， ① \\ 2 x + 3 y - z = 8 ， ② \\ 3 x - 2 y + z = 3 ， ③ \end{array}$
小曹同学的部分解答过程如下：
解：______+______，得3x+4y=10，④
______+______，得5x+y=11，⑤
______与______联立，得方程组
${\begin{array}{l} 3 x + 4 y = 10 \\ 5 x + y = 11 \end{array}$

(1)、请你在方框中补全小曹同学的解答过程：

(2)、若m、n、p、q满足方程组 ${\begin{array}{l} m + n + p + q = 4 \\ 2 (m + n) + 3 p - q = 16 \\ 3 (m + n) - 2 p + q = 6 \end{array}$ ，则m+n-2p+q= ．

查看试题解析
19. 计算：

(1)、3a•（-a²）+a⁴÷a

(2)、（2x-y）（x+3y）

(3)、（a-b+1）（a-b-1）

查看试题解析
20. 把下列各式分解因式：

(1)、2a（m+n）-b（m+n）

(2)、2x²y-8xy+8y

查看试题解析
21. 解方程组：

(1)、 ${\begin{matrix} x + y = 3, ① \\ 3 x - y = 1, ② \end{matrix}$

(2)、若（1）中方程组的解也是关于x，y的方程ax+by=5的解，且a，b为正整数，则a^b=

查看试题解析
22. 如图，三角形ABC的顶点A，B，C都在格点（正方形网格线的交点）上，将三角形ABC向左平移2格，再向上平移3格，得到三角形A'BC“（设点A、B、C分别平移到A′、B′、C′）

(1)、请在图中画出平移后的三角形A'B′C′；

(2)、若连接BB′、CC′，则这两条线段的位置关系是．数量关系是

(3)、若BB'与AC相交于点P，则∠A'B'P，∠B'PA与∠PAB三个角之间的数量关系为
A．∠A'B'P+∠B'PA+∠PAB=180°

B．∠A'B'P+∠B'PA+∠PAB=360°

C．∠A'B'P+∠B'PA-∠PAB=180°

D．∠A'B'P+∠B'PA-∠PAB=360°

查看试题解析
23. 如图，CE⊥DG，垂足为G，∠BAF=50°，∠ACE=140°．CD与AB平行吗？为什么？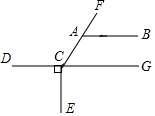

查看试题解析
24. 填写下列空格
已知：如图，点E在BC上，BD⊥AC，EF⊥AC，垂足分别为D、F，点M、G在AB上，

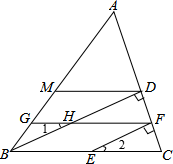
∠AMD=∠AGF，∠1=∠2．

求证：DM∥BC

证明：∵BD⊥AC，EF⊥AC，垂足分别为D、F（已知）

∴∠BDC=90°，∠EFC=90°（垂直的定义）

∴∠BDC=∠EFC（等量代换）

∴（同位角相等，两直线平行）

∠2=∠CBD（）

∠1=∠2（已知）

∠1=∠CBD（）

∴（）

∴∠AMD=∠AGF（已知）

∴DM∥GF（同位角相等，两直线平行）

∴DM∥BC（）

查看试题解析
25. 如图，点B在线段AC上，分别以线段AC、AB、BC为直径画圆，圆心分别是点O、O₁、O₂ ．已知半径O₁A=acm，半径O₂C比半径O₁A大bcm．

(1)、O₂C=cm（用含a、b的代数式表示）OA=cm（用含a、b的代数式表示）；

(2)、求图中阴影部分的面积（π取3）．

查看试题解析
26. 借助图形直观，感受数与形之间的关系，我们常常可以发现一些重要结论．
初步应用

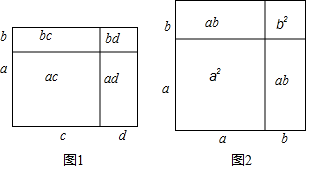(1)、①如图1，大长方形的面积可以看成4个小长方形的面积之和，由此得到多项式乘多项式的运算法，则（用图中字母表示）
②如图2，借助①，写出一个我们学过的公式：（用图中字母表示）

(2)、深入探究
仿照图2，构造图形并计算（a+b+c）²

(3)、拓展延伸
借助以上探究经验，解决下列问题：

①代数式（a₁+a₂+a₂+a₃+a₄+a₅）²展开、合并同类项后，得到的多项式的项数一共有项；

②若正数x、y、z和正数m、n、p，满足x+m=y+n=z+p=t，请通过构造图形比较px+my+nz与t²的大小（画出图形，并说明理由）；

③已知x、y、z满足x+y+z=2m，x²+y²+z²=2n，xyz=p，求x²y²+y²z²+x²z²的值（用含m、n、P的式子表示）

查看试题解析