江苏省常州市金坛区2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2020-04-30 类型:期中考试
一、单选题
-
1. 下列计算结果为x6的是( )A、x7﹣x B、x2+x4 C、(x4)2 D、x7÷x2. 下列计算正确的是( )A、 B、 C、 D、3. 计算 的结果是( )A、 B、 C、 D、4. 多项式 分解因式的结果是( )A、 B、 C、 D、5. 如图,AB∥CD,∠1=45°,∠3=80°,则∠2的度数为( )
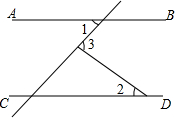 A、30° B、35° C、40° D、45°6. 如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是( )
A、30° B、35° C、40° D、45°6. 如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是( )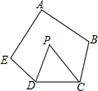 A、60° B、55° C、50° D、45°7. 已知x﹣y=3,y﹣z=2,x+z=4,则代数式x2﹣z2的值是( )A、9 B、18 C、20 D、248. 计算 ,结果是( )A、 B、 C、 D、
A、60° B、55° C、50° D、45°7. 已知x﹣y=3,y﹣z=2,x+z=4,则代数式x2﹣z2的值是( )A、9 B、18 C、20 D、248. 计算 ,结果是( )A、 B、 C、 D、二、填空题
-
9. 计算: .10. 计算: .11. 计算:(a+1)2﹣a2= .12. 若a+b=4,ab=1,则a2b+ab2= .13. 在人体血液中,红细胞直径约为 ,数据0.00077用科学记数法表示为 .14. 若3n=5,则32n=.15. 将两张三角形纸片如图摆放,量得∠1+∠2+∠3+∠4=220°,则∠5=.
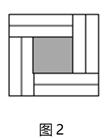
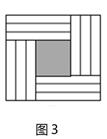
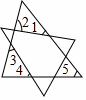 16. 用若干个形状、大小完全相同的长方形纸片围成正方形,4个长方形纸片围成如图1所示的正方形,其涂色部分的面积是25;8个长方形纸片围成如图2所示的正方形,其涂色部分的面积是16;12个长方形纸片围成如图3所示的正方形,其涂色部分的面积是.
16. 用若干个形状、大小完全相同的长方形纸片围成正方形,4个长方形纸片围成如图1所示的正方形,其涂色部分的面积是25;8个长方形纸片围成如图2所示的正方形,其涂色部分的面积是16;12个长方形纸片围成如图3所示的正方形,其涂色部分的面积是.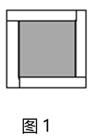
三、解答题
-
17. 计算:(1)、(2)、(3)、18. 求下列代数式的值:(1)、 ,其中 ;(2)、 ,其中 .19. 把下列各式分解因式:(1)、 ;(2)、 ;(3)、 .20. 如图, 是锐角三角形.
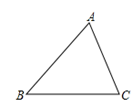 (1)、过点 画 的垂线,垂足为 ;过点 画 的垂线,交 的延长线于点 .(2)、在所画图中, 是哪些直角三角形的高?21. 如图,在 中,点 、 分别在 、 上, , , , 与 有怎样的位置关系?为什么?
(1)、过点 画 的垂线,垂足为 ;过点 画 的垂线,交 的延长线于点 .(2)、在所画图中, 是哪些直角三角形的高?21. 如图,在 中,点 、 分别在 、 上, , , , 与 有怎样的位置关系?为什么?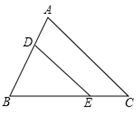 22. 如图, 是 的角平分线,点 、 分别在 、 上,且 , . 与 相等吗?为什么?
22. 如图, 是 的角平分线,点 、 分别在 、 上,且 , . 与 相等吗?为什么? 23. 有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案:
23. 有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案: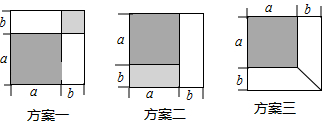
小明发现这三种方案都能验证公式:a2+2ab+b2=(a+b)2 , 对于方案一,小明是这样验证的:
a2+ab+ab+b2=a2+2ab+b2=(a+b)2
请你根据方案二、方案三,写出公式的验证过程.
方案二:
方案三:
24.(1)、填空:① .② .
③ .
(2)、猜想下列各题的结果并验证下列第②个等式:① .
② .
25. 阅读下列材料并解答问题:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“3倍角三角形”例如:一个三角形三个内角的度数分别是 ,这个三角形就是一个“3倍角三角形”.反之,若一个三角形是“3倍角三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.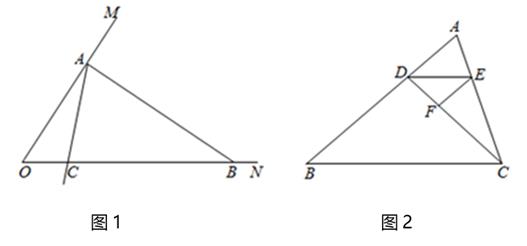 (1)、如图1,已知 ,在射线 上取一点 ,过点 作 交 于点 .判断 是否是“3倍角三角形”,为什么?(2)、在(1)的条件下,以 为端点画射线 ,交线段 于点 (点 不与点 、点 重合).若 是“3倍角三角形”,求 的度数.(3)、如图2,点 在 的边上,连接 ,作 的平分线交 于点 ,在 上取一点 ,使得 , .若 是“3倍角三角形”,求 的度数.
(1)、如图1,已知 ,在射线 上取一点 ,过点 作 交 于点 .判断 是否是“3倍角三角形”,为什么?(2)、在(1)的条件下,以 为端点画射线 ,交线段 于点 (点 不与点 、点 重合).若 是“3倍角三角形”,求 的度数.(3)、如图2,点 在 的边上,连接 ,作 的平分线交 于点 ,在 上取一点 ,使得 , .若 是“3倍角三角形”,求 的度数.