江苏省盐城市东台市第四教育联盟2019届九年级下学期数学期中考试试卷
试卷更新日期:2020-04-30 类型:期中考试
一、单选题
-
1. 绝对值为 4 的实数是( )A、±4 B、4 C、-4 D、22. 下列多边形中,既是轴对称图形又是中心对称图形的是( )A、平行四边形 B、正方形 C、直角三角形 D、等边三角形3. 下列立体图形中,主视图是三角形的是( )。A、
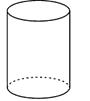 B、
B、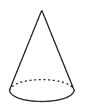 C、
C、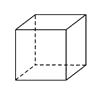 D、
D、 4. 太阳与地球的平均距离大约是150 000 000千米,数据150 000 000用科学记数法表示为( )A、1.5×108 B、1.5×109 C、0.15×109 D、15×1075. 下列计算正确的是( )A、2x-x=1 B、x2•x3=x6 C、(-xy3)2=x2y6 D、(m-n)2=m2-n26. 若一组数据3、4、5、x、6、7的平均数是5,则x的值是( )A、5 B、6 C、7 D、87. 如图,在 中, , ,则 的度数是( )
4. 太阳与地球的平均距离大约是150 000 000千米,数据150 000 000用科学记数法表示为( )A、1.5×108 B、1.5×109 C、0.15×109 D、15×1075. 下列计算正确的是( )A、2x-x=1 B、x2•x3=x6 C、(-xy3)2=x2y6 D、(m-n)2=m2-n26. 若一组数据3、4、5、x、6、7的平均数是5,则x的值是( )A、5 B、6 C、7 D、87. 如图,在 中, , ,则 的度数是( ) A、 B、 C、 D、8. 已知x1、x2是关于x的方程x2﹣ax﹣2=0的两根,下列结论一定正确的是( )A、x1≠x2 B、x1+x2>0 C、x1•x2>0 D、x1<0,x2<0
A、 B、 C、 D、8. 已知x1、x2是关于x的方程x2﹣ax﹣2=0的两根,下列结论一定正确的是( )A、x1≠x2 B、x1+x2>0 C、x1•x2>0 D、x1<0,x2<0二、填空题
-
9. 如果收入15元记作+15元,那么支出20元记作元.10. 在函数y= 中,自变量x的取值范围是 .11. 多项式 4a﹣a3 分解因式为.12. 如图,一只蚂蚁在半径为1的⊙O内随机爬行,若四边形ABCD是⊙O的内接正方形,则蚂蚁停在中间正方形内概率为.
 13. 如图,已知 , , ,则 .
13. 如图,已知 , , ,则 . 14. 如图,反比例函数y= (k≠0,x>0)的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为8,则k的值为.
14. 如图,反比例函数y= (k≠0,x>0)的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为8,则k的值为. 15. 半径为2的圆被四等分切割成四条相等的弧,将四个弧首尾顺次相连拼成如图所示的恒星图型,那么这个恒星的面积等于.
15. 半径为2的圆被四等分切割成四条相等的弧,将四个弧首尾顺次相连拼成如图所示的恒星图型,那么这个恒星的面积等于.
三、解答题
-
16. 计算:2sin30°﹣(π﹣ )0+| ﹣1|+( )﹣117. 解不等式组: .18. 先化简,再求值:(1﹣ )÷ ,其中a=﹣3.19. 甲、乙两人玩“石头、剪刀、布”的游戏.(1)、用树状图或列表法列出该游戏的所有可能结果;(2)、求在一次比赛时两人做同种手势的概率.20. 某校为了解学生对“第二十届中国哈尔滨冰雪大世界”主题景观的了解情况,在全体学生中随机抽取了部分学生进行调查,并把调查结果绘制成如图的不完整的两幅统计图:
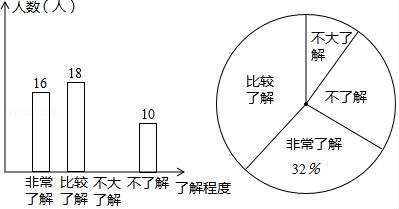 (1)、本次调查共抽取了多少名学生;(2)、通过计算补全条形图;(3)、若该学校共有750名学生,请你估计该学校选择“比较了解”项目的学生有多少名?21. 已知:如图,在▱ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)、本次调查共抽取了多少名学生;(2)、通过计算补全条形图;(3)、若该学校共有750名学生,请你估计该学校选择“比较了解”项目的学生有多少名?21. 已知:如图,在▱ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.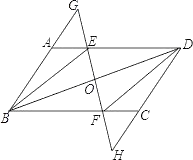 (1)、求证:△ABE≌△CDF;(2)、连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.22. 某景区商店销售一种纪念品,每件的进货价为40元.经市场调研,当该纪念品每件的销售价为50元时,每天可销售200件;当每件的销售价每增加1元,每天的销售数量将减少10件.(1)、当每件的销售价为52元时,该纪念品每天的销售数量为件;(2)、当每件的销售价x为多少时,销售该纪念品每天获得的利润y最大?并求出最大利润.23. 某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
(1)、求证:△ABE≌△CDF;(2)、连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.22. 某景区商店销售一种纪念品,每件的进货价为40元.经市场调研,当该纪念品每件的销售价为50元时,每天可销售200件;当每件的销售价每增加1元,每天的销售数量将减少10件.(1)、当每件的销售价为52元时,该纪念品每天的销售数量为件;(2)、当每件的销售价x为多少时,销售该纪念品每天获得的利润y最大?并求出最大利润.23. 某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数
10
15
20
…
x
方式一的总费用(元)
150
175
…
方式二的总费用(元)
90
135
…
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
24. 如图,△ABC内接于⊙O,CD是⊙O的直径,AB与CD交于点E,点P是CD延长线上的一点,AP=AC,且∠B=2∠P. (1)、求证:PA是⊙O的切线;(2)、若PD= ,求⊙O的直径;(3)、在(2)的条件下,若点B等分半圆CD,求DE的长.25. 如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD、CE的交点.
(1)、求证:PA是⊙O的切线;(2)、若PD= ,求⊙O的直径;(3)、在(2)的条件下,若点B等分半圆CD,求DE的长.25. 如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD、CE的交点. (1)、判断线段BD与CE的关系,并证明你的结论;(2)、若AB=8,AD=4,把△ADE绕点A旋转,
(1)、判断线段BD与CE的关系,并证明你的结论;(2)、若AB=8,AD=4,把△ADE绕点A旋转,①当∠EAC=90°时,求PB的长;
②求旋转过程中线段PB长的最大值.
26. 如图,已知直线AB经过点(0,4),与抛物线y= x2交于A,B两点,其中点A的横坐标是 .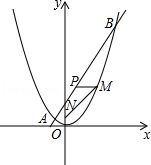 (1)、求这条直线的函数关系式及点B的坐标.(2)、在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在请说明理由.(3)、过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
(1)、求这条直线的函数关系式及点B的坐标.(2)、在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在请说明理由.(3)、过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?