江苏省南通市海门市2019届九年级下学期数学期中考试试卷（一模）

试卷更新日期：2020-04-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 3的绝对值为（）

A、 3 B、 $- 3$ C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 江苏省南通市总面积约有8544平方公里，将数8544用科学记数法表示为（　　）

A、854.4×10 B、85.44×10² C、8.544×10³ D、0.8544×10⁴

查看试题解析
3. 如图，已知数轴上的点A，O，B，C，D分别表示数﹣2，0，1，2，3，则表示数 $\sqrt{2}$ 的点P应落在线段（　　）

A、AO上 B、OB上 C、BC上 D、CD上

查看试题解析
4. 一个不透明的盒子中装有9个除颜色外其他完全相同的乒乓球，其中3个是黄球，6个是白球.从该盒子中任意摸出一个球，摸到黄球的概率是（　　）

A、 $\frac{1}{3}$ B、 $\frac{2}{5}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
5. 下列运算正确的是（　　）

A、3x²+4x²=7x⁴ B、2x³·3x³=6x³ C、x⁶÷x³=x² D、（x²）⁴=x⁸

查看试题解析
6. 如图，将一副三角板叠放在一起，使直角顶点重合于点O，∠A＝60°，∠D＝45°，AB∥OC，DC与OB交于点E，则∠DEO的度数为（　　）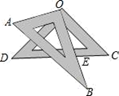

A、85° B、80° C、75° D、65°

查看试题解析
7. 某件商品原价为1000元，连续两次都降价x%后该件商品售价为640元，则下列所列方程正确的是（　　）

A、1000（1﹣x%）²＝640 B、1000（1﹣x%）²＝360 C、1000（1﹣2x%）＝640 D、1000（1﹣2x%）＝360

查看试题解析
8. 如图，小东在同一平面上按照如下步骤进行尺规作图：
（ 1 ）作线段AB，分别以A，B为圆心，以AB长为半径作弧，两弧交于点C；

（ 2 ）以C为圆心，以AB长为半径作弧交AC的延长线于点D；

（ 3 ）连接BD，BC.则下列说法中不正确的是（　　）

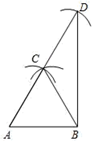A、∠ABD＝90° B、sin²A+cos²D＝1 C、DB＝ $\sqrt{3}$ AB D、点C是△ABD的外心

查看试题解析
9. 甲、乙两车都从A地出发，都匀速行驶至B地，先到达的车停在B地休息.在整个行驶过程中，甲、乙两车离开A地的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示.根据图中提供的信息，有下列说法：①A，B两地相距300千米；②甲车比乙车早出发1小时，且晚1小时到达B地；③乙车只用了1.5小时就追上甲车；④当甲、乙两车相距40千米时，t＝ $\frac{2}{3}$ ， $\frac{3}{2}$ ， $\frac{7}{2}$ 或 $\frac{13}{3}$ 小时.其中正确的说法有（　　）

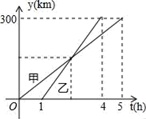A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 在平面直角坐标系xOy中，点O（0，0），A（2，0），B（0，2 $\sqrt{3}$ ），C（﹣2，0）.将△OAB绕点O顺时针旋转α（0°＜α＜360°）得到△OA′B′（（其中点A旋转到点A′的位置），设直线AA′与直线BB′相交于点P，则线段CP长的最小值是（　　）

A、2 $\sqrt{2} - 2$ B、2 $\sqrt{3} - 2$ C、2 D、2 $\sqrt{5} - 2$

查看试题解析

二、填空题

11. 如果分式 $\frac{2}{x - 1}$ 有意义，那么x的取值范围是．

查看试题解析
12. 分解因式： $a^{3} - {4ab}^{2} =$ .

查看试题解析
13. 如图是一个几何体的三视图（图中尺寸单位：cm），根据图中所示数据求得这个几何体的侧面积是cm².

查看试题解析
14. 请你阅读下面的诗句：“栖树一群鸦，鸦树不知数，三只栖一树，五只没去处，五只栖一树，闲了一棵树，请你仔细数，鸦树各几何？”若诗句中谈到的鸦为x只，树为y棵，则可列出方程组为.

查看试题解析
15. 设α，β是方程x²﹣x﹣2019＝0的两个实数根，则α²+αβ+β²的值为.

查看试题解析
16. 如图，已知小华、小强的身高分别为1.8m，1.6m，小华、小强之间的水平距离为15.6m，小华、小强在同一盏路灯下的影长分别为4m，3.2m，则这盏路灯的高度为m.

查看试题解析
17. 如图，已知半径为4cm的扇形OAB，其圆心角∠AOB＝45°，将它沿射线OA方向作无滑动滚动，当第一次滚动到扇形O′A′B′的位置时，点O运动到点O′所经过的路径长为cm.

查看试题解析
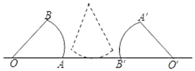18. （在平面直角坐标系xOy中，抛物线y＝ax²+4ax+4a+1（a＜0）交x轴于A，B两点，若此抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）有且只有8个整点（横、纵坐标都是整数的点），则a的取值范围是.

查看试题解析

三、解答题

19.

(1)、计算： $- 2^{- 2} - {(π - 3)}^{\circ} + | \sqrt{3} - 3 | + 2 \cos 30^{°}$ ；

(2)、先化简，再求值： $(1 - \frac{1}{x}) \div \frac{x - 1}{x + 1} - \frac{x + 2}{x + 1}$ ，其中3x²+3x﹣2＝0.

查看试题解析
20. 解不等式组： ${\begin{array}{l} 2 x + 5 ≻ 3 (x + 1) \\ 4 x ≻ \frac{- x - 9}{2} \end{array}$ ，并把它的解集在数轴上表示出来.

查看试题解析
21. 如图， $▱$ ABCD中，点E是BC边的一点，延长AD至点F，使∠DFC＝∠DEC.
求证：四边形DECF是平行四边形.

查看试题解析

22. 阅读对每个人成长的影响是巨大的，一本好书往往能改变人的一生，每年的4月23日被联合国教科文组织确定为“世界读书日”.某初中倡导学生课外读书，下面的表格是该校学生去年阅读课外书籍情况统计表，如图是该校初中三个年级学生人数分布的扇形统计图，其中八年级学生人数为612人，请你根据图表中提供的信息，解答下列问题：

图书种类	频数	频率
科普常识	2520	b
名人传记	2448	c
中外名著	a	0.25
其　　他	432	0.06

(1)、求该校初中三个年级学生的总人数；

(2)、求表中a，b，c的值；

(3)、问该校学生去年读课外书籍的平均本数是否超过4.5？请说明理由.

查看试题解析

23. 如图，甲船在港口P的南偏西60°方向，距港口80海里的A处，沿AP方向以每小时18海里的速度匀速驶向港口P.乙船从港口P出发，沿南偏东45°方向匀速驶离港口P，已知两船同时出发，经过2小时乙船恰好在甲船的正东方向.求乙船的行驶速度.（结果保留根号）

查看试题解析
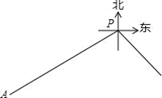24. 在平面直角坐标系xOy中，直线y＝﹣2x与双曲线y＝ $\frac{k}{x}$ 的一个交点为P（ $- \sqrt{3}$ ，m）.

(1)、求k的值；

(2)、将直线y＝﹣2x向下平移b（b＞0）个单位长度时，与x轴，y轴分别交于点A，点B，与双曲线y＝ $\frac{k}{x}$ 的其中一个交点记为Q.若BQ＝2AB，求b的值.

查看试题解析
25. 如图，△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，交AC于点E，过点D作DF⊥AC于点F，交AB的延长线于点G.

(1)、若AB＝10，BC＝12，求△DFC的面积；

(2)、若tan∠C＝2，AE＝6，求BG的长.

查看试题解析
26. 已知关于x的一元二次方程mx²﹣（2m+1）x+2＝0.

(1)、当m取何值时，此方程有两个不相等的实数根；

(2)、当抛物线y＝mx²﹣（2m+1）x+2与x轴两个交点的横坐标均为整数，且m为负整数时，求此抛物线的解析式；

(3)、在（2）的条件下，若P（n，y₁），Q（n+1，y₂）是此抛物线上的两点，且y₁＞y₂ ，请结合函数图象直接写出实数n的取值范围.

查看试题解析
27. 如图，边长为1的正方形ABCD中，点E、F分别在边CD、AD上，连接BE、BF、EF，且有AF+CE＝EF.

(1)、求（AF+1）（CE+1）的值；

(2)、探究∠EBF的度数是否为定值，并说明理由；

(3)、将△EDF沿EF翻折，若点D的对应点恰好落在BF上，求EF的长.

查看试题解析
28. 定义：在平面直角坐标系xOy中，对于点P和图形M，如果线段OP与图形M有公共点时，就称点P为关于图形M的“亲近点”.
已知平面直角坐标系xOy中，点A（1， $\sqrt{3}$ ），B（5， $\sqrt{3}$ ），连接AB.

(1)、在P₁（1，2），P₂（3，2），P₃（5，2）这三个点中，关于线段AB的“亲近点”是；

(2)、若线段CD上的所有点都是关于线段AB的“亲近点”，点C（t，2 $\sqrt{3} t - 3 \sqrt{3}$ ）、D（t+6，2 $\sqrt{3} t - 3 \sqrt{3}$ ），求实数t的取值范围；

(3)、若⊙A与y轴相切，直线l：y＝ $- \sqrt{3} x + b$ 过点B，点E是直线l上的动点，⊙E半径为2，当⊙E上所有点都是关于⊙A的“亲近点”时，直接写出点E横坐标n的取值范围.

查看试题解析