江苏省无锡市江阴市澄东片2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-04-30 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图标既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在一次有24000名学生参加的数学质量抽测的成绩中，随机取2000名考生的数学成绩进行分析，则在该抽样中，样本指的是（）.

A、所抽取的2000名考生的数学成绩 B、24000名考生的数学成绩 C、2000 D、2000名考生

查看试题解析
3. 在 $\frac{1}{x}$ , $\frac{1}{2}$ , $\frac{x^{2} + 1}{2}$ , $\frac{3 x y}{π}$ , $\frac{3}{x + y}$ ,a+ $\frac{1}{m}$ 中，分式的个数是（　　）

A、2 B、3 C、4 D、5

查看试题解析
4. 下列关于矩形的说法中正确的是（　　）

A、对角线相等的四边形是矩形 B、矩形的对角线相等且互相平分 C、对角线互相平分的四边形是矩形 D、矩形的对角线互相垂直且平分

查看试题解析
5. 如果把 $\frac{5 x}{x + y}$ 中的x与y都扩大为原来的5倍，那么这个代数式的值（　　）

A、不变 B、扩大为原来的5倍 C、缩小为原来的 $\frac{1}{5}$ D、扩大为原来的10倍

查看试题解析
6. 某工厂现在平均每天比原计划多生产50台机器，现在生产600台所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x台机器，根据题意，下面所列方程正确的是（　　）

A、 $\frac{600}{x - 50}$ ＝ $\frac{450}{x}$ B、 $\frac{600}{x + 50}$ ＝ $\frac{450}{x}$ C、 $\frac{600}{x}$ ＝ $\frac{450}{x + 50}$ D、 $\frac{600}{x}$ ＝ $\frac{450}{x - 50}$

查看试题解析
7. 如图，在▱ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，若AB＝6，EF＝2，则BC的长为（）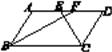

A、8 B、10 C、12 D、14

查看试题解析
8. 如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，CE＝5，F为DE的中点.若△CEF的周长为18，则OF的长为（　　）

A、3 B、4 C、 $\frac{5}{2}$ D、 $\frac{7}{2}$

查看试题解析
9. 若关于x的分式方程 $\frac{x}{x - 3}$ ＝2﹣ $\frac{m}{3 - x}$ 有增根，则m的值为（　　）

A、﹣3 B、2 C、3 D、不存在

查看试题解析
10. 如图，正方形ABCD的边长为1，AC，BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH，HG交AB于点E，连接DE交AC于点F，连接FG。则下列结论：
①四边形AEGF是菱形                  ②△AED≌△GED
③∠DFG=112.5°                       ④BC+FG=1.5
其中正确的结论是（    ）

A、①②③④ B、①②③ C、①② D、②

查看试题解析

二、填空题

11. 若分式 $\frac{x - 2}{x}$ 的值是0，则x的值为．

查看试题解析
12. 已知菱形两条对角线的长分别为6cm和8cm，则这个菱形的面积是cm².

查看试题解析
13. 要反映无锡一周内每天的最高气温的变化情况，宜采用统计图．

查看试题解析
14. 在四边形ABCD中，AB=DC，AD=BC，请再添加一个条件，使四边形ABCD是矩形．你添加的条件是．（写出一种即可）

查看试题解析
15. 关于x的方程 $\frac{2 x + a}{x - 1} = 1$ 的解是正数，则a的取值范围是．

查看试题解析
16. 如图，在△ABC中，∠BAC＝33°，将△ABC绕点A按顺时针方向旋转50°，对应得到△AB′C′，则∠B′AC的度数为．

查看试题解析
17. 如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则CF的长度为

查看试题解析
18. 如图，已知∠XOY=60°，点A在边OX上，OA=2.过点A作AC⊥OY于点C，以AC为一边在∠XOY内作等边三角形ABC，点P是△ABC围成的区域（包括各边）内的一点，过点P作PD∥OY交OX于点D，作PE∥OX交OY于点E.设OD=a，OE=b，则a+2b的取值范围是.

查看试题解析

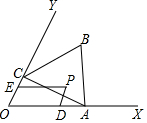
三、解答题

19. 计算或化简

(1)、 $\frac{a^{2} - 1}{a} \div \frac{a^{2} - a}{a^{2}}$

(2)、 $\frac{x^{2}}{x - 1} + \frac{x}{1 - x}$

查看试题解析
20. 如图，在平行四边形ABCD中，E为BC的中点，连接DE.延长DE交AB的延长线于点F.求证：AB=BF.

查看试题解析
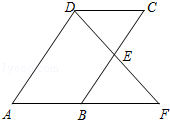21. 某中学对全校学生进行文明礼仪知识测试，为了解测试结果，随机抽取部分学生的成绩进行分析，将成绩分为三个等级：不合格、一般、优秀，并绘制成如图两幅统计图（不完整）.

请你根据图中所给的信息解答下列问题：

(1)、这次测试，一共抽取了名学生；

(2)、请将以上两幅统计图补充完整；（注：扇形图补百分比，条形图补“优秀”人数与高度）；

(3)、若“一般”和“优秀”均被视为达标成绩，该校学生有1200人，请你估计此次测试中，全校达标的学生有多少人.

查看试题解析
22. 在8×8的正方形网格中建立如图所示的平面直角坐标系，已知A（2，4）、B（4，2）.C是第一象限内的一个格点，点C与线段AB可以组成一个以AB为底，且腰长为无理数的等腰三角形.

(1)、填空：点C的坐标是， △ABC的面积是.

(2)、将△ABC绕点C旋转180°得到△A₁B₁C₁连接AB₁、BA₁ ，试判断四边形AB₁A₁B是何种特殊四边形，画图并说明理由.

查看试题解析
23. 某品牌牛奶专营店销售一款牛奶，售价是在进价的基础上加价a%出售，每月的销售额可以达到9.6万元，但每月需支出2.45万元的固定费用及进价的2.5%的其它费用.如果该款牛奶每月所获的利润要达到1万元，那么a的值是多少？（利润=售价-进价-固定费用-其它费用）

查看试题解析
24. 如图，矩形OABC的边OA在x轴正半轴上，边OC在y轴正半轴上，B点的坐标为（1，3）.矩形O'A'BC'是矩形OABC绕B点逆时针旋转得到的.O'点恰好在x轴的正半轴上，O'C'交AB于点D.

(1)、求点O'的坐标，并判断△O'DB的形状（要说明理由）

(2)、求边C'O'所在直线的解析式.

(3)、延长BA到M使AM=1，在（2）中求得的直线上是否存在点P，使得ΔPOM是以线段OM为直角边的直角三角形?若存在，请直接写出P点的坐标；若不存在，请说明理由.

查看试题解析
25. 先化简，再求值： $\frac{4}{a^{2} - 4} - \frac{1}{a - 2}$ ，其中a=1．

查看试题解析
26. 解下列方程：

(1)、 $\frac{1}{x - 1} = \frac{1}{x^{2} - 1}$

(2)、 $\frac{2}{3}$ + $\frac{x}{3 x - 1}$ = $\frac{1}{9 x - 3}$

查看试题解析