江苏省苏州市吴江区2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2020-04-30 类型:期中考试
一、单选题
-
1. 下列调查中,适合普查的是( )A、一批手机电池的使用寿命 B、你所在学校的男、女同学的人数 C、中国公民保护环境的意识 D、端午节期间泰兴市场上粽子的质量2. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若点A(-1,6)在反比例函数 的图像 上,则k的值是( )A、-6 B、-3 C、3 D、64. 若分式 的值为零,则( )A、x=3 B、x=﹣3 C、x=2 D、x=﹣25. 下列命题中,假命题是( )A、一组对边相等的四边形是平行四边形 B、三个角是直角的四边形是矩形 C、四边相等的四边形是菱形 D、有一个角是直角的菱形是正方形6. 下列事件中,属于随机事件的是( )A、抛掷1个均匀的骰子,出现6点向上 B、在一个仅装着白球和黑球的袋中摸出红球 C、任意三角形的内角和为180° D、13人中至少有2人的生日在同一个月7. 已知点 都在反比例函数 的图像上,则下列关系式一定正确的是( )A、 B、 C、 D、8. 一列列车自全国铁路第5次大提速后,速度提高了26千米/时,现在该列车从甲站到乙站所用的时间比原来减少了1小时,已知甲、乙两站的路程是312千米,若设列车提速前的速度是x千米/时,则根据题意所列方程正确的是( )
3. 若点A(-1,6)在反比例函数 的图像 上,则k的值是( )A、-6 B、-3 C、3 D、64. 若分式 的值为零,则( )A、x=3 B、x=﹣3 C、x=2 D、x=﹣25. 下列命题中,假命题是( )A、一组对边相等的四边形是平行四边形 B、三个角是直角的四边形是矩形 C、四边相等的四边形是菱形 D、有一个角是直角的菱形是正方形6. 下列事件中,属于随机事件的是( )A、抛掷1个均匀的骰子,出现6点向上 B、在一个仅装着白球和黑球的袋中摸出红球 C、任意三角形的内角和为180° D、13人中至少有2人的生日在同一个月7. 已知点 都在反比例函数 的图像上,则下列关系式一定正确的是( )A、 B、 C、 D、8. 一列列车自全国铁路第5次大提速后,速度提高了26千米/时,现在该列车从甲站到乙站所用的时间比原来减少了1小时,已知甲、乙两站的路程是312千米,若设列车提速前的速度是x千米/时,则根据题意所列方程正确的是( )
A、 B、 C、 D、9. 如图, 中, 分别是 的中点,点 在 上,且 ,当 时, 的长是( )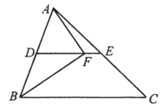 A、9 B、10.5 C、12 D、1810. 如图, 和 都是等腰直角三角形, ,反比例函数 的图像经过点 若 与 的面积之差 ,则 的值为( )
A、9 B、10.5 C、12 D、1810. 如图, 和 都是等腰直角三角形, ,反比例函数 的图像经过点 若 与 的面积之差 ,则 的值为( )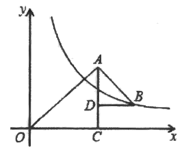 A、2 B、4 C、6 D、8
A、2 B、4 C、6 D、8二、填空题
-
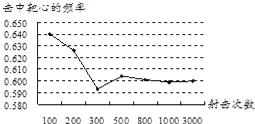
11. 若分式 有意义,则 的取值范围是.12.
如图,是某射手在相同条件下进行射击训练的结果统计图,该射手击中靶心的概率的估计值为 .
 13. 反比例函数 的图像经过点 ,则在每一个象限内, 随 的增大而. (填“增大”或“减小”)14. 若关于 的方程 产生增根,则 的值为15. 在平面直角坐标系 中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标(1,0),顶点A的坐标为(0, 2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点 的坐标为
13. 反比例函数 的图像经过点 ,则在每一个象限内, 随 的增大而. (填“增大”或“减小”)14. 若关于 的方程 产生增根,则 的值为15. 在平面直角坐标系 中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标(1,0),顶点A的坐标为(0, 2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点 的坐标为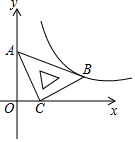 16. 如图,连接四边形 各边中点得到四边形 ,还要添加才能使四边形 是菱形.(只需写出一个即可)
16. 如图,连接四边形 各边中点得到四边形 ,还要添加才能使四边形 是菱形.(只需写出一个即可)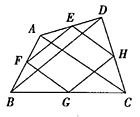 17. 如图,在平面直角坐标系中,函数 与 的图象交 于 两点,过 作 轴的垂线,交函数 的图象于点 ,连接 ,则 的面积为.
17. 如图,在平面直角坐标系中,函数 与 的图象交 于 两点,过 作 轴的垂线,交函数 的图象于点 ,连接 ,则 的面积为.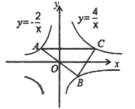 18. 如图,在四边形 中, , 是 的中点点 以每秒1个单位长度的速度从点 出发,沿 向点 运动;点 同时以每秒3个单位长度的速度从点 出发,沿 向点 运动.点 停止运动时,点 也随之停止运动.当运动时间 秒时,以点 为顶点的四边形是平行四边形.则 的值为.
18. 如图,在四边形 中, , 是 的中点点 以每秒1个单位长度的速度从点 出发,沿 向点 运动;点 同时以每秒3个单位长度的速度从点 出发,沿 向点 运动.点 停止运动时,点 也随之停止运动.当运动时间 秒时,以点 为顶点的四边形是平行四边形.则 的值为.
三、解答题
-
19. 计算与化简:20. 解方程:21. 先化简、再求值: ,其中 .22. 如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系 的原点 在格点上, 轴、 轴都在格线上.线段 的两个端点也在格点上.
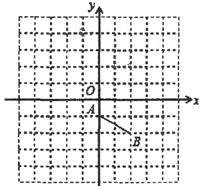
①若将线段 绕点 逆时针旋转90°得到线段 ,试在图中画出线段 .
②若线段 与线段 关于 轴对称,请画出线段 .
③若点 是此平面直角坐标系内的一点,当点 四边围成的四边形为平行四边形时,请你直接写出点 的坐标(写出一个即可).
23. 某学校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目供学生选择.为了估计全校学生对这四个活动项目的选择情况,体育老师从全体学生中随机抽取了部分学生进行调查(规定每人必须并且只能选择其中的一个项目),并把调查结果绘制成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题: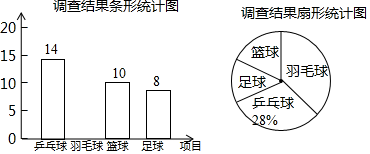 (1)、求参加这次调查的学生人数,并补全条形统计图;(2)、求扇形统计图中“篮球”项目所对应扇形的圆心角度数;(3)、若该校共有2000名学生,试估计该校选择“足球”项目的学生有多少人?24. 如图,在▱ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)、求参加这次调查的学生人数,并补全条形统计图;(2)、求扇形统计图中“篮球”项目所对应扇形的圆心角度数;(3)、若该校共有2000名学生,试估计该校选择“足球”项目的学生有多少人?24. 如图,在▱ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.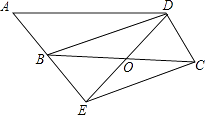 (1)、求证:四边形BECD是平行四边形;(2)、若∠A=50°,则当∠BOD=°时,四边形BECD是矩形.25. 高铁苏州北站已于几年前投入使用,计划在广场内种植A.B两种花木共2000棵,若种植A种花木的数量比种植B种花木数量的3倍多400棵。(1)、求种植A.B两种花木的数量分别是多少棵?(2)、如果园林处安排12人同时种植这两种花木,每人每天能种植A种花木40棵或B种花木30棵,应分别安排多少人种植A种花木和B种花木,才能确保同时完成各自的任务?26. 如图,在矩形ABCD中,AD=4,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF.
(1)、求证:四边形BECD是平行四边形;(2)、若∠A=50°,则当∠BOD=°时,四边形BECD是矩形.25. 高铁苏州北站已于几年前投入使用,计划在广场内种植A.B两种花木共2000棵,若种植A种花木的数量比种植B种花木数量的3倍多400棵。(1)、求种植A.B两种花木的数量分别是多少棵?(2)、如果园林处安排12人同时种植这两种花木,每人每天能种植A种花木40棵或B种花木30棵,应分别安排多少人种植A种花木和B种花木,才能确保同时完成各自的任务?26. 如图,在矩形ABCD中,AD=4,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF.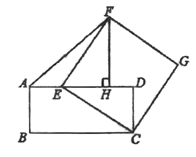 (1)、求证:FH=ED;(2)、当AE为何值时,△AEF的面积最大?
(1)、求证:FH=ED;(2)、当AE为何值时,△AEF的面积最大?

