江苏省南通市如皋市2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2020-04-30 类型:期中考试
一、单选题
-
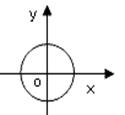
1. 下列曲线中能表示 是 的函数的是( )A、
 B、
B、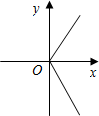 C、
C、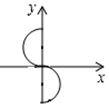 D、
D、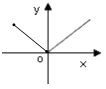 2. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
2. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:甲
乙
丙
丁
平均数(cm)
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表数据,从中选择一名成绩好且发挥稳定的参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁3. 正方形具有而菱形不具有的性质是( )A、四边相等 B、四角相等 C、对角线互相平分 D、对角线互相垂直4. 已知点A(1,y1),B(-3,y2)都在直线 上,则( )A、y1< y2 B、y1= y2 C、y1>y2 D、不能比较5. 如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于E,若∠EAO=15°,则∠BOE的度数为( ) A、85° B、80° C、75° D、70°6. 如图,四边形ABCD是菱形, ,DB=6,DH⊥AB于H,则DH等于( )
A、85° B、80° C、75° D、70°6. 如图,四边形ABCD是菱形, ,DB=6,DH⊥AB于H,则DH等于( ) A、 B、 C、5 D、47. 如图,已知直线y=3x+b与y=ax-2的交点的横坐标为-2,根据图象有下列3个结论:①a>0;②b>0;③x>-2是不等式3x+b>ax-2的解集.其中正确的个数是( )
A、 B、 C、5 D、47. 如图,已知直线y=3x+b与y=ax-2的交点的横坐标为-2,根据图象有下列3个结论:①a>0;②b>0;③x>-2是不等式3x+b>ax-2的解集.其中正确的个数是( ) A、0 B、1 C、2 D、38. 如图,在平面直角坐标系中,▱OABC的顶点A在x轴上,顶点B的坐标为(6,4).若直线l经过点(1,0),且将▱OABC分割成面积相等的两部分,则直线l的函数解析式是( )
A、0 B、1 C、2 D、38. 如图,在平面直角坐标系中,▱OABC的顶点A在x轴上,顶点B的坐标为(6,4).若直线l经过点(1,0),且将▱OABC分割成面积相等的两部分,则直线l的函数解析式是( ) A、y=x+1 B、 C、y=3x﹣3 D、y=x﹣19. 甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:
A、y=x+1 B、 C、y=3x﹣3 D、y=x﹣19. 甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:①A、B之间的距离为1200m;②乙行走的速度是甲的1.5倍;③b=960;④a=34.以上结论正确的有( )
 A、①② B、①②③ C、①③④ D、①②④10. 如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )
A、①② B、①②③ C、①③④ D、①②④10. 如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )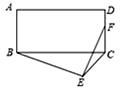 A、 B、4 C、5 D、
A、 B、4 C、5 D、二、填空题
-
11. 某校规定学生的体育成绩由三部分组成;体育技能测试占50%,体育理论测试占20%,体育课外活动表现30%,甲同学的上述三部分成绩依次为96分,85分,90分,则甲同学的体育成绩为分.12. 一组数据:80,75,85,90,80的中位数是.13. 直线y=3x+2沿y轴向下平移6个单位,则平移后直线解析式为.14. 如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是三边的中点,CF=8cm,则线段DE=cm.
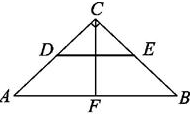 15. 含45°角的直角三角板如图放置在平面直角坐标系中,其中A(-3,0),B(0,2),则直线BC的解析式为.
15. 含45°角的直角三角板如图放置在平面直角坐标系中,其中A(-3,0),B(0,2),则直线BC的解析式为. 16. 已知正方形ABCD的边长为4,点E,F分别在AD,DC上,AE=DF=1,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为.
16. 已知正方形ABCD的边长为4,点E,F分别在AD,DC上,AE=DF=1,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为.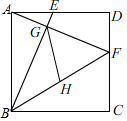 17. 不论m取何值,点P(2m,m+1)都在某一条直线上,则这条直线的解析式是.18. 如图,在平面直角坐标系中,点 ,点 ,点P是直线 上一点,且 ,则点P的坐标为 .
17. 不论m取何值,点P(2m,m+1)都在某一条直线上,则这条直线的解析式是.18. 如图,在平面直角坐标系中,点 ,点 ,点P是直线 上一点,且 ,则点P的坐标为 .
三、解答题
-
19. 已知y与3x+1成正比例,且x=3时,y=4.求y与x之间的函数关系式.20. 已知▱ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:四边形AECF为平行四边形.
 21. 如图,在矩形ABCD中,BD的垂直平分线分别交AB、CD、BD于E、F、O,连接DE、BF.
21. 如图,在矩形ABCD中,BD的垂直平分线分别交AB、CD、BD于E、F、O,连接DE、BF. (1)、求证:四边形BEDF是菱形;(2)、若AB=16cm,BC=8cm,求四边形DEBF的面积.22. 某校初二开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)、求证:四边形BEDF是菱形;(2)、若AB=16cm,BC=8cm,求四边形DEBF的面积.22. 某校初二开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示: (1)、根据图示填写下表:
(1)、根据图示填写下表:班级
中位数(分)
众数(分)
平均数(分)
爱国班
85
求知班
100
85
(2)、结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?(3)、已知爱国班复赛成绩的方差是70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定?23. 如图,直线y=- x+b与x轴交于点A,与y轴交于点B,与直线y=x交于点E,点E的横坐标为3. (1)、求点E的坐标和b的值;(2)、在x轴上有点P(m,0),过点P作x轴的垂线,与直线y=- x+b交于点C,与直线y=x交于点D.若CD≤4,求m的取值范围.24. 春节期间,某商场计划购进甲、乙两种商品,两种商品进价分别为30元、70元,商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,设购进甲商品x件,这100件商品的销售总利润为y元.(1)、求y与x的函数关系式;(2)、请你设计获利最大的进货方案,并求出最大利润.25. 如图1所示,在A,B两地之间有汽车站C站,客车由C站驶往A地,到达A地后立即原速驶往B地,货车由B地驶往A地,两车同时出发,匀速行驶.图2是客车、货车离C站的距离y(千米)与行驶时间x(小时)之间的函数关系图象,请结合图象信息解答下列问题:
(1)、求点E的坐标和b的值;(2)、在x轴上有点P(m,0),过点P作x轴的垂线,与直线y=- x+b交于点C,与直线y=x交于点D.若CD≤4,求m的取值范围.24. 春节期间,某商场计划购进甲、乙两种商品,两种商品进价分别为30元、70元,商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,设购进甲商品x件,这100件商品的销售总利润为y元.(1)、求y与x的函数关系式;(2)、请你设计获利最大的进货方案,并求出最大利润.25. 如图1所示,在A,B两地之间有汽车站C站,客车由C站驶往A地,到达A地后立即原速驶往B地,货车由B地驶往A地,两车同时出发,匀速行驶.图2是客车、货车离C站的距离y(千米)与行驶时间x(小时)之间的函数关系图象,请结合图象信息解答下列问题: (1)、A,B两地间的距离是千米;请直接在图2中的括号内填上正确数字;(2)、求货车由B地驶往A地过程中,y与x之间的函数关系式,并写出自变量x的取值范围;(3)、客、货两车出发多长时间,距各自出发地的距离相等?直接写出答案;(4)、客、货两车出发多长时间,相距500千米?直接写出答案.26. 在四边形ABCD中,对角线AC、BD相交于点O,过点O的直线分别交边AB、CD、AD、BC于点E、F、G、H
(1)、A,B两地间的距离是千米;请直接在图2中的括号内填上正确数字;(2)、求货车由B地驶往A地过程中,y与x之间的函数关系式,并写出自变量x的取值范围;(3)、客、货两车出发多长时间,距各自出发地的距离相等?直接写出答案;(4)、客、货两车出发多长时间,相距500千米?直接写出答案.26. 在四边形ABCD中,对角线AC、BD相交于点O,过点O的直线分别交边AB、CD、AD、BC于点E、F、G、H
(感知)如图①,若四边形ABCD是正方形,且EF⊥GH,易知S△BOE=S△AOG , 又因为S△AOB= S四边形ABCD , 所以S四边形AEOG= S正方形ABCD(不要求证明);
(1)、(拓展)如图②,若四边形ABCD是矩形,且S四边形AEOG= S矩形ABCD , 若AB=a,AD=b,BE=m,求AG的长(用含a、b、m的代数式表示);
(2)、(探究)如图③,若四边形ABCD是平行四边形,且S四边形AEOG= S▱ABCD , 若AB=3,AD=5,BE=1,则AG=.