江苏省海门市东洲国际2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-04-30 类型：期中考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点 $P (- 1, 3)$ 关于 $y$ 轴对称点的坐标为（）

A、（1,3） B、（-1,-3） C、（-1,3） D、（1,-3）

查看试题解析
2. 下列给出的条件中，能判断四边形ABCD是平行四边形的是（）

A、AB∥CD，AD = BC； B、∠B = ∠C；∠A = ∠D， C、AB =CD，CB = AD； D、AB = AD，CD = BC

查看试题解析
3. 若O是四边形ABCD对角线的交点且OA=OB=OC=OD，则四边形ABCD是（）

A、平行四边形 B、矩形 C、正方形 D、菱形

查看试题解析
4. 解一元二次方程x²＋4x－1＝0，配方正确的是（）

A、 ${(x + 2)}^{2} = 3$ B、 ${(x - 2)}^{2} = 3$ C、 ${(x + 2)}^{2} = 5$ D、 ${(x - 2)}^{2} = 5$

查看试题解析
5. 一元二次方程（x﹣1）（x﹣2）=0的解是（）

A、x=1 B、x=2 C、x₁=1，x₂=2 D、x₁=﹣1，x₂=﹣2

查看试题解析
6. 对于函数y=2x﹣1，下列说法正确的是（　　）

A、它的图象过点（1，0） B、y值随着x值增大而减小 C、当y＞0时，x＞1 D、它的图象不经过第二象限

查看试题解析
7. 已知一组数据x₁,x₂,x₃,x₄,x₅,的方差是2，那么数据3x₁+2，3x₂+2，3x₃+2，3x₄+2，3x₅+2方差是（）

A、2 B、6 C、8 D、18

查看试题解析
8. 已知直线 $y = (m - 3) x - 3 m + 1$ 不经过第一象限，则 $m$ 的取值范围是 $x$ （）.

A、 $m \geq \frac{1}{3}$ B、 $m \leq \frac{1}{3}$ C、 $\frac{1}{3} < m < 3$ D、 $\frac{1}{3} \leq m \leq 3$

查看试题解析
9. 如图，四边形ABCD是正方形，直线l₁ ， l₂ ， l₃分别通过A，B，C三点，且l₁∥l₂∥l₃ ，若l₁与l₂的距离为5，l₂与l₃的距离为7，则正方形ABCD的面积等于（）

A、70 B、74 C、144 D、148

查看试题解析
10. 如图，在等腰△ABC中， $∠ A C B = 90^{°}$ ， $A C = 8$ ，F是AB边上的中点，点D，E分别在AC，BC边上运动，且保持 $A D = C E$ ，连接DE，DF，EF在此运动变化的过程中，下列结论：（1） $△ D E F$ 是等腰直角三角形； $(2)$ 四边形CDFE不可能为正方形，（3） $D E$ 长度的最小值为4；（4）连接CF，CF恰好把四边形CDFE的面积分成1：2两部分，则 $C E =$ $\frac{1}{3}$ 或 $\frac{14}{3}$ 其中正确的结论个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 函数y= $\frac{1}{x - 2}$ 中，自变量x的取值范围是．

查看试题解析
12. 数据1,2,3,4,5的方差是．

查看试题解析
13. 已知▱ABCD中，若∠B+∠D＝200°，则∠A的度数为.

查看试题解析
14. 点（﹣2，y₁），（﹣1，y₂），（1，y₃）都在直线y=﹣3x+b上，则y₁ ， y₂ ， y₃的大小关系是．

查看试题解析
15. 如图，四边形ABCD中，E，F，G，H分别是边AB、BC、CD、DA的中点．若四边形EFGH为菱形，则对角线AC、BD应满足条件．

查看试题解析
16. 如图，已知函数y＝3x+b和y＝ax﹣3的图象交于点P（﹣2，﹣5），则根据图象可得不等式3x+b＞ax﹣3的解集是.

查看试题解析
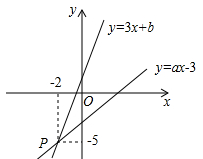17. 关于x的方程kx²- 2x + 1=0有两个实数根，那么实数k的取值范围是.

查看试题解析
18. 已知A（-1，1），B（1，1），在直线y = - x+4上找一点P，使PA+PB最小，则点P坐标为.

查看试题解析

三、解答题

19. 解方程

(1)、 $x^{2} + 2 x - 3 = 0$

(2)、x（x-2）=3（2-x）

查看试题解析
20. 已知，直线y=2x+3与直线y=﹣2x﹣1.

(1)、求两直线与y轴交点A，B的坐标；

(2)、求两直线交点C的坐标；

(3)、求△ABC的面积.

查看试题解析
21. 如图，将▱ABCD的对角线BD向两个方向延长至点E和点F，使BE=DF，证：四边形AECF是平行四边形.

查看试题解析
22. 某市为了节约生活用水，计划制定每位居民统一的月用水量标准，然后根据标准，实行分段收费.为此，对居民上年度的月均用水量进行了抽样调查，并根据调查结果绘制了上年度月均用水量的频数分布直方图（图中分组含最低值，不含最高值），请根据图中信息解答下列问题：

(1)、本次调查的居民人数为人；

(2)、本次调查的居民月均用水量的中位数落在频数分布直方图中的第小组内（从左至右数）；

(3)、当地政府希望让85%左右居民的月均用水量低于制定的月用水量标准，根据上述调查结果，你认为月用水量标准（取整数）定为多少吨时较为合适？

查看试题解析
23. 已知▱ABCD中，A（1，3），B（2，-1），C（5，-5）

(1)、D的坐标为.

(2)、若经过原点的一条直线平分▱ABCD的面积，求此直线的解析式

查看试题解析
24. 规定：如果两个一次函数的一次项系数和常数项互换，即y=kx+b和y=bx+k（其中|k|≠|b|），称这样的两个一次函数为互助一次函数，例如 $y = - 2 x + \frac{1}{3}$ 和 $y = \frac{1}{3} x - 2$ 就是互助一次函数.根据规定解答下列问题：

(1)、填空：一次函数 $y = - \frac{1}{4} x + 4$ 与它的互助一次函数的交点坐标为

(2)、若两个一次函数y=（k-b）x–k-2b与 $y = (k - 3) x + 3 k - \frac{5}{2}$ 是互助一次函数，求两函数图象与y轴围成的三角形的面积.

查看试题解析
25. 甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地，如图，线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系；折线BCD表示轿车离甲地距离y（千米）与x（小时）之间的函数关系.请根据图象解答下列问题：

(1)、轿车到达乙地后，货车距乙地多少千米？

(2)、求线段CD对应的函数解析式.

(3)、轿车到达乙地后，马上沿原路以CD段速度返回，求货车从甲地出发后多长时间再与轿车相遇（结果精确到0.01）.

查看试题解析
26. 2018雾霾天气趋于严重，某商场根据民众健康需要，从厂家购进了A，B两种型号的空气净化器，如果销售15台A型和10台B型空气净化器的利润为6000元，销售10台A型和15台B型空气净化器的利润为6500元.

(1)、求每台A型空气净化器和B型空气净化器的销售利润；

(2)、该商场计划一次购进两种型号的空气净化器共160台，其中B型空气净化器的进货量不超过A型空气净化器的2倍，设购进A型空气净化器x台，这160台空气净化器的销售总利润为y元.
①求y关于x的函数关系式；

②该公司购进A型、B型空气净化器各多少台时，才能使销售总利润最大？

查看试题解析
27. 如图，直线l₁： $y = \frac{4}{3} x + 4$ 分别与x轴、y轴交于A、B两点，点C为x轴上任意一点，直线l₂： $y = - \frac{3}{4} x + b$ 经过点C，且与直线l₁交于点D，与y轴交于点E，连结AE.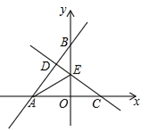

(1)、当点C的坐标为 $(2 ， 0)$ 时，①求直线l₂的函数表达式；
②求证：AE平分 $∠ B A C$ ；

(2)、问：是否存在点C，使 $△ A C E$ 是以CE为一腰的等腰三角形？若存在，直接写出点C的坐标；若不存在，请说明理由.

查看试题解析
28. 如图1，在平面直角坐标系中，直线y=- $\frac{1}{2}$ x+3与x轴、y轴相交于A、B两点，点C在线段OA上，将线段CB绕着点C顺时针旋转90°得到CD，此时点D恰好落在直线AB上，过点D作DE⊥x轴于点E.

(1)、求证：△BOC≌△CED；

(2)、如图2，将△BCD沿x轴正方向平移得△B'C'D'，当B'C'经过点D时，求△BCD平移的距离及点D的坐标；

(3)、若点P在y轴上，点Q在直线AB上，是否存在以C、D、P、Q为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的P点的坐标；若不存在，请说明理由.

查看试题解析