江苏省常州市溧阳市2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-04-30 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
2. 下列事件中最适合使用普查方式收集数据的是（）

A、了解某班同学的身高情况 B、了解全市每天丢弃的废旧电池数 C、了解50发炮弹的杀伤半径 D、了解我省农民的年人均收入情况

查看试题解析
3. 下列从左到右变形正确的是（　　）

A、 $\frac{a}{b} = \frac{a + c}{b + c}$ B、 $\frac{a}{b}$ ＝ $\frac{a^{2}}{b^{2}}$ C、 $\frac{a}{b}$ ＝ $\frac{ac}{bc}$ D、 $\frac{ac}{bc}$ ＝ $\frac{a}{b}$

查看试题解析
4. 下列分式 $\frac{a}{a b}, \frac{4}{2 m + 4}, \frac{x + π}{x}, \frac{b^{2} - 4}{b - 2}, \frac{a + b}{b - a}$ 中，最简分式的个数是（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 把分式 $\frac{x}{2 x + y}$ 中的x和y都扩大2倍，则分式的值（　　）

A、扩大4倍 B、扩大2倍 C、缩小2倍 D、不变

查看试题解析
6. 四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件：①AD∥BC；②AD=BC；③OA=OC；④OB=OD，从中任选两个条件，能使四边形ABCD为平行四边形的选法有（）．

A、3种 B、4种 C、5种 D、6种

查看试题解析
7. 下列判断中正确的是（　　）

A、对角线互相垂直的四边形是菱形 B、三个角相等的四边形是矩形 C、对角线相等的平行四边形是正方形 D、对角线互相垂直的矩形是正方形

查看试题解析
8. 如图，在菱形ABCD中，AB＝4cm，∠ADC＝120°，点E、F同时由A，C两点出发，分别沿AB，CB方向向点B匀速移动（到点B为止），点E的速度为1cm/s，点F的速度为2cm/s，经过t秒△DEF为等边三角形，则t的值为（　　）

A、1s B、 $\frac{3}{4}$ s C、 $\frac{4}{3}$ s D、2s

查看试题解析

二、填空题

9. 当x＝时，分式 $\frac{1 - x^{2}}{x - 1}$ 的值是0.

查看试题解析
10. 如果菱形的两条对角线长分别为6和8，那么这个菱形一边上的高是.

查看试题解析
11. 分式 $\frac{1}{3 x}$ ，﹣ $\frac{3}{4 x^{2} y}$ ， $\frac{x}{12 y^{2}}$ 的最简公分母是.

查看试题解析
12. 在一个不透明的布袋中装有红色、白色玻璃球共40个，除颜色外其他完全相同，小明通过多次摸球试验后发现，其中摸到红色球的频率稳定在0.15左右，则口袋中红色球可能有个.

查看试题解析
13. 如图，P是等边△ABC内的一点，PB＝2cm，PC＝3cm，AB＝4cm，若将△BCP绕点B按逆时针方向旋转到△ABP′，则PP′＝.

查看试题解析
14. 如图， $▱$ ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点，若AC+BD=24厘米，△OAB的周长是18厘米，则EF=厘米.

查看试题解析
15. 如图，过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ，那么图中矩形AMKP的面积S₁与矩形QCNK的面积S₂的大小关系是S₁S₂；（填“＞”或“＜”或“＝”）

查看试题解析
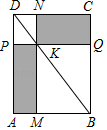16. 已知正方形ABCD的边长为4，点E，F分别在AD，DC上，AE＝DF＝1，BE与AF相交于点G，点H为BF的中点，连接GH，则GH的长为.

查看试题解析
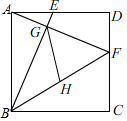17. 如图，已知AB＝2 $\sqrt{2}$ ，C为线段AB上的一个动点，分别以AC，CB为边在AB的同侧作菱形ACED和菱形CBGF，点C，E，F在一条直线上，∠D＝120°.P、Q分别是对角线AE，BF的中点，当点C在线段AB上移动时，点P，Q之间的距离最短为（结果保留根号）.

查看试题解析
18. 如图，在正方形ABCD的外部作∠AED＝45°，且AE＝6，DE＝3，连接BE，则BE＝.

查看试题解析

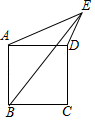
三、解答题

19. 计算：

(1)、 $\frac{a^{2}}{b^{2} c}$ （﹣ $\frac{b c^{2}}{2 a}$ ）

(2)、 $\frac{a + 2}{a - 3}$ × $\frac{2 a - 6}{a^{2} - 4}$

(3)、 $\frac{x^{2}}{2 x - 4}$ ﹣ $\frac{2}{x - 2}$

(4)、 $\frac{x - 3}{x - 2}$ ÷（x+2﹣ $\frac{5}{x - 2}$ ）

查看试题解析
20. 先化简： $(\frac{a - 2}{a^{2} + 2 a} - \frac{a - 1}{a^{2} + 4 a + 4}) \div \frac{a - 4}{a + 2}$ ，再选一个你喜欢的a的值代入求值.

查看试题解析

21. 为弘扬中华传统文化，某校组织八年级800名学生参加汉字听写大赛为了解学生整体听写能力，从中抽取部分学生的成绩（得分取正整数，满分为100分）进行统计分析，得到如下所示的模数分布表：

分数段	50.5～60.5	60.5～70.5	70.5～80.5	80.5～90.5	90.5～100.5
频数	16	30	50	m	24
所占百分比	8%	15%	25%	40%	n

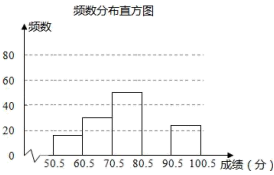
请根据尚未完成的表格，解答下列问题：

(1)、本次抽样调查的样本容量为，表中m＝.

(2)、补全图中所示的频数分布直方图.

(3)、若成绩超过80分为优秀，则该校八年级学生中汉字听写能力优秀的约有多少人?

查看试题解析

22. 如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣3，2），B（0，4），C（0，2）.

(1)、将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A₁B₁C；平移△ABC，若点A的对应点A₂的坐标为（1，﹣4），画出平移后对应的△A₂B₂C₂；

(2)、若将△A₁B₁C绕某一点旋转可以得到△A₂B₂C₂；请直接写出旋转中心的坐标；

(3)、在x轴上有一点P，使得PA+PB的值最小，请直接写出点P的坐标.

查看试题解析
23. 如图，△ABC中，AB＝AC，∠BAC＝100°，将△ABC绕点A顺时针方向旋转40°得到△ADE，BC与AD、DE交于点G、F.

(1)、求∠AGC的度数；

(2)、求证：四边形ABFE是菱形.

查看试题解析
24. 如图，平行四边形ABCD中，对角线AC、BD相交于点O，AD＝ $\frac{1}{2}$ DB，点E、F、G分别是AO、BO、DC的中点，连接EF、DE、EG、GF.

(1)、求证：四边形DEFG是平行四边形；

(2)、求证：EG＝EF.

查看试题解析
25. 在平面直角坐标系xOy中，点M的坐标为（x₁ ， y₁），点的坐标为（x₂ ， y₂），且x₁≠x₂ ， y₁≠y₂ ，以MN为边构造菱形，若该菱形的两条对角分平行于x轴、y轴，则称该菱形为边的“坐标菱形”.

(1)、已知点A（2，0），B（0，3），则以AB为边的“坐标菱形”的面积为；

(2)、若点C（1，2），点D在直线x＝5上，以CD为边的“坐标菱形”为正方形，求直线CD的函数表达式.

查看试题解析
26. 如图，在矩形ABCD中，AB＝4，BC＝3，点Q在BC上，BQ＝2，点P是AB上的一个动点，连接PQ，将△PBQ沿PQ翻折，点B落在点B′.

(1)、当AP＝时，四边形PBQB′的面积是矩形面积的 $\frac{1}{2}$ ；

(2)、当AP为何值时，四边形PBQB′是正方形？为什么？

(3)、在翻折过程中是否存在AP的值，使得点B′与矩形对称中心点O重合，如果存在，请求出AP的值；如果不存在，请说明理由.

查看试题解析