湖北省黄冈市十校联考2020届九年级下学期数学期中考试试卷
试卷更新日期：2020-04-30 类型：期中考试
一、单选题
-
1. 在实数－3、0、5、3中，最小的实数是（ ）A、－3 B、0 C、5 D、32. 下列运算正确的是（ ）A、a3•a＝a3 B、（﹣2a2）3＝﹣6a5 C、a5＋a5＝a10 D、8a5b2÷2a3b＝4a2b3.
如图，是由一个圆柱体和一个长方体组成的几何体．其主视图是（ ）
A、
B、
C、
D、
4. 一把直尺和一块三角板ABC（含30°、60°角）摆放位置如图所示，直尺一边与三角板的两直角边分别交于点D、点E，另一边与三角板的两直角边分别交于点F、点A，且∠CDE=40°，那么∠BAF的大小为（ ）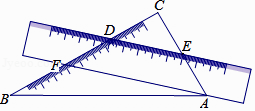
A、40° B、45° C、50° D、10°5. 如图，在△ABC中，AB＝AC，∠A＝30°，AB的垂直平分线l交AC于点D，则∠CBD的度数为（ ）
A、30° B、45° C、50° D、75°6. 甲、乙两人从少年宫出发，沿相同的路线分别以不同的速度匀速跑向体育馆，甲先跑一段路程后，乙开始出发，当乙超出甲150米时，乙停在此地等候甲，两人相遇后乙又继续以原来的速度跑向体育馆.如图是甲、乙两人在跑步的全过程中经过的路程y（米）与甲出发的时间x（秒）的函数图象，则乙在途中等候甲用了（ ）秒
A、200 B、150 C、100 D、80二、填空题
-
7. 根据中央“精准扶贫”规划，每年要减贫约11700000人，将数据11700000用科学记数法表示为 ．8. 计算： =.9. 若关于x的分式方程 =2的解为负数，则k的取值范围为 ．
10. 如图，一个宽为2 cm的刻度尺在圆形光盘上移动，当刻度尺的一边与光盘相切时，另一边与光盘边缘两个交点处的读数恰好是“2”和“10”（单位：cm），那么该光盘的直径是cm.
11. 用半径为12cm，圆心角为90°的扇形纸片围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为cm．12.两个全等的三角尺重叠放在△ACB的位置，将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置，使点A恰好落在边DE上，AB与CE相交于点F．已知∠ACB=∠DCE=90°，∠B=30°，AB=8cm，则CF=cm．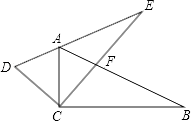
13. 已知关于x的二次函数y=ax2+（a2-1）x-a的图象与
轴的一个交点的坐标为（m，0），若2<m<3，则a的取值范围是. 14. 因式分解： ＝.三、解答题
-
15. 解不等式组 ，并写出它的所有整数解．16. 如图，在△ABC中，AD是BC边上的中线，点E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF．
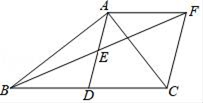(1)、求证：△AEF≌△DEB；(2)、若∠BAC＝90°，求证：四边形ADCF是菱形．17. 为迎接”抗战胜利70周年纪念展”，中国国家博物馆进行了合并改扩建工程.新馆的展厅总面积与原馆大楼的总建筑面积相同，成为目前世界上最大的博物馆.已知原馆大楼的总建筑面积比原馆大楼的展览面积的3倍少0.4万平方米，新馆的展厅总面积比原馆大楼的展览面积大4.2万平方米，求新馆的展厅总面积和原馆大楼的展览面积.18. 已知关于x的一元二次方程 .(1)、求证：该方程有两个不等的实根；(2)、若该方程的两个实数根 、 满足 ，求m的值.19. 我县实施新课程改革后，学习的自主字习、合作交流能力有很大提高，张老师为了了解所教班级学生自主学习、合作交流的具体情况，对本班部分学生进行了为期半个月的跟踪调査，并将调査结果分成四类，A：特别好；B：好；C：一般；D：较差；并将调査结果绘制成以下两幅不完整的统计图，请你根据统计图下列问题：
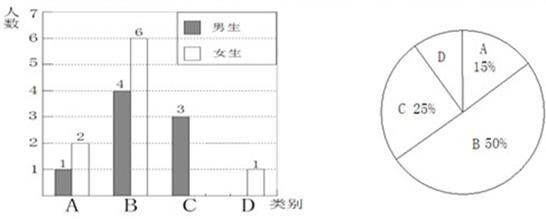(1)、本次调查中，张老师一共调査了名同学，其中C类女生有名，D类男生有名；(2)、将上面的条形统计图补充完整；(3)、为了共同进步，张老师想从被调査的A类和D类学生中分别选取一位同学迸行“一帮一”互助学习，请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．20. 如图，直角坐标系中，直线 与反比例函数 的图象交于A，B两点，已知A点的纵坐标是2.
(1)、求反比例函数的解析式.(2)、将直线 沿x轴向右平移6个单位后，与反比例函数在第二象限内交于点C.动点P在y轴正半轴上运动，当线段PA与线段PC之差达到最大时，求点P的坐标.21. AB为⊙O直径，BC为⊙O切线，切点为B，CO平行于弦AD，作直线DC.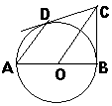
(1)、求证：DC为⊙O切线；(2)、若AD·OC=8，求⊙O半径.22.如图所示，某办公大楼正前方有一根高度是15米的旗杆ED，从办公楼顶端A测得旗杆顶端E的俯角α是45°，旗杆底端D到大楼前梯坎底边的距离DC是20米，梯坎坡长BC是12米，梯坎坡度i=1： ，求大楼AB的高度是多少？（精确到0.1米，参考数据： ≈1.41， ≈1.73， ≈2.45）
23. 为鼓励大学毕业生自主创业，某市政府出台了相关政策：由政府协调，本市企业按成本价提供产品给大学毕业生自主销售，成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件
元，出厂价为每件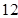 
元，每月销售量y（件）与销售单价x（元）之间的关系近似满足一次函数： . (1)、李明在开始创业的第一个月将销售单价定为20元，那么政府这个月为他承担的总差价为多少元?(2)、设李明获得的利润为W（元），当销售单价定为多少元时，每月可获得最大利润?(3)、物价部门规定，这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元，那么政府为他承担的总差价最少为多少元?24. 在△ABC中，∠C＝90°，AC＝3，BC＝4，CD是斜边AB上的高，点E在斜边AB上，过点E作直线与△ABC的直角边相交于点F，设AE＝x，△AEF的面积为y.
(1)、CD= ， AD=；(2)、若EF⊥AB，当点E在线段AB上移动时；①求y与x的函数关系式；（写出自变量x的取值范围）
②当x取何值时，y有最大值？并求其最大值
(3)、若F在直角边AC上（点F与A、C两点均不重合），点E在斜边AB上移动，试问：是否存在直线EF将△ABC的周长和面积同时平分？若存在直线EF，求出x的值；若不存在直线EF，请说明理由.