天津市和平区2019届高三理数第三次质量调查试卷
试卷更新日期:2020-04-30 类型:高考模拟
一、单选题
-
1. 设集合 , ,则 ( )A、 B、 C、 D、2. 设 , ,则 是 的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件3. 设 , 满足约束条件 ,则 的取值范围是( )A、 B、 C、 D、4. 在如图所示的计算 程序框图中,判断框内应填入的条件是( )
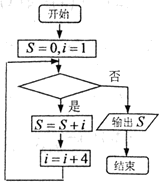 A、 B、 C、 D、5. 已知菱形 的边长为2, ,点 , 分别在边 , 上, , ,若 ,则 的值为( )A、3 B、2 C、 D、6. 若函数 的图象关于 对称,则函数 在 上的最小值是( )A、 B、 C、 D、7. 设 , 分别为具有公共焦点 , 的椭圆和双曲线的离心率, 为两曲线的一个公共点,且满足 ,则 的值为( )A、 B、 C、2 D、不确定8. 已知函数 , ,若方程 有两个不同的实数根,则实数 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、5. 已知菱形 的边长为2, ,点 , 分别在边 , 上, , ,若 ,则 的值为( )A、3 B、2 C、 D、6. 若函数 的图象关于 对称,则函数 在 上的最小值是( )A、 B、 C、 D、7. 设 , 分别为具有公共焦点 , 的椭圆和双曲线的离心率, 为两曲线的一个公共点,且满足 ,则 的值为( )A、 B、 C、2 D、不确定8. 已知函数 , ,若方程 有两个不同的实数根,则实数 的取值范围是( )A、 B、 C、 D、二、填空题
-
9. 若 ,其中 , 是虚数单位,则 .10. 由曲线 , 以及 轴围成的封闭图形面积为 .11. 已知两条不重合的直线 , ,两个不重合的平面 , ,有下列四个命题:
①若 , ,则 ;
②若 , ,且 ,则 ;
③若 , , , ,则 ;
④若 , ,且 , ,则 .
其中所有正确命题的序号为 .
12. 已知曲线 的参数方程为 ( 为参数), 是曲线 的焦点,点 的极坐标为 ,曲线 上有某点 ,使得 取得最小值,则点 的坐标为 .13. 已知 , ,且 ,则 最小值为 .14. 用1,2,3,4,5,6组成六位数(没有重复数字),要求任何相邻两个数字的奇偶性不同,且1和2不相邻,这样的六位数的个数是(用数字作答)。三、解答题
-
15. 在△ABC中,角A,B,C的对边分别为a,b,c , 且 .(1)、求A的值;(2)、若B=30°,BC边上的中线AM= ,求△ABC的面积.16. 某城市为鼓励人们乘坐地铁出行,地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策,不超过30站的地铁票价如下表:
乘坐站数
票价(元)
3
6
9
现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过30站,甲、乙乘坐不超过10站的概率分别为 , ;甲、乙乘坐超过20站的概率分别为 , .
(Ⅰ)求甲、乙两人付费相同的概率;
(Ⅱ)设甲、乙两人所付费用之和为随机变量 ,求 的分布列和数学期望.
17. 如图,在四棱锥 中, 平面 ,底面 是菱形, , .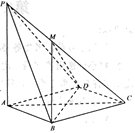
(Ⅰ)求证:直线 平面 ;
(Ⅱ)求直线 与平面 所成角的正切值;
(Ⅲ)设点 在线段 上,且二面角 的余弦值为 ,求点 到底面 的距离.