北京市昌平区2019届高三理数5月二模试卷

试卷更新日期：2020-04-30 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知全集 $U = R$ ，集合 $A = {x | x^{2} \leq 1}$ ，则 $C_{U} A = =$ （）

A、 $(- \infty, - 1) \cup (1, + \infty)$ B、 $(- \infty, - 1] \cup [1, + \infty)$ C、 $(- 1, 1)$ D、 $[- 1, 1]$

查看试题解析
2. 已知复数 $z = - 1 + a (1 + i)$ （i为虚数单位，a为实数）在复平面内对应的点位于第二象限，则复数z的虚部可以是（）

A、 $- \frac{1}{2} i$ B、 $\frac{1}{2} i$ C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
3. 已知某程序框图如图所示，则执行该程序后输出的a的值是（）

A、 $- 1$ B、 $\frac{1}{2}$ C、1 D、2

查看试题解析
4. 若直线 $y = 2 x$ 上存在点 $(x ， y)$ 满足 ${\begin{array}{l} x + y - 3 \leq 0 ， \\ x - 2 y - 3 \geq 0 ， \\ x \geq m ， \end{array}$ 则实数 $m$ 的最大值为（）

A、 $- 2$ B、 $- 1$ C、 $1$ D、 $3$

查看试题解析
5. 设 $\overset{⇀}{a}, \overset{⇀}{b}$ 是非零向量，则“存在实数 $λ$ ，使得 $\overset{⇀}{a} = λ \overset{⇀}{b}$ ”是“ $| \overset{⇀}{a} + \overset{⇀}{b} | = | \overset{⇀}{a} | + | \overset{⇀}{b} |$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
6. 某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（）

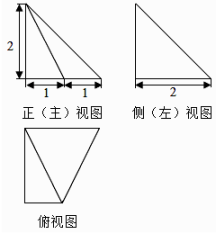A、1 B、2 C、3 D、4

查看试题解析
7. 嫦娥四号月球探测器于2018年12月8日搭载长征三号乙运载火箭在西昌卫星发射中心发射.12日下午4点43分左右，嫦娥四号顺利进入了以月球球心为一个焦点的椭圆形轨道，如图中轨道③所示，其近月点与月球表面距离为 $100$ 公里，远月点与月球表面距离为 $400$ 公里.已知月球的直径为 $3476$ 公里，则该椭圆形轨道的离心率约为（）

A、 $\frac{1}{25}$ B、 $\frac{3}{40}$ C、 $\frac{1}{8}$ D、 $\frac{3}{5}$

查看试题解析
8. 已知函数 $f (x)$ 是定义在 $R$ 上的偶函数，且满足 $f (x) = {\begin{array}{l} x^{2} - \frac{x}{2} (0 \leq x < 1) ， \\ \frac{x - 1}{e^{x}} (x \geq 1) \end{array}$ ，若函数 $F (x) = f (x) - m$ 有6个零点，则实数 $m$ 的取值范围是（）

A、 $(- \frac{1}{16} ， \frac{1}{e^{2}})$ B、 $(- \frac{1}{16} ， 0) \cup (0 ， \frac{1}{e^{2}})$ C、 $(0 ， \frac{1}{e^{2}})$ D、 $[0 ， \frac{1}{e^{2}})$

查看试题解析

二、填空题

9. 已知幂函数 $y = f (x)$ 的图像过点 $(2, \sqrt{2}),$ 则 $f (4) =$ ．

查看试题解析
10. 在极坐标系中，极点到直线 $ρ \cos θ + ρ \sin θ = 2$ 的距离为.

查看试题解析
11. 在 $△ A B C$ 中，三边长分别为 $a = 3, b = 2 \sqrt{2}, c = \sqrt{5}$ ,其最大角的余弦值为, $△ A B C$ 的面积为.

查看试题解析
12. 2019年3月2日，昌平 “回天”地区开展了 $7$ 种不同类型的 “三月雷锋月,回天有我”社会服务活动. 其中有 $2$ 种活动既在上午开展、又在下午开展， $3$ 种活动只在上午开展， $2$ 种活动只在下午开展 . 小王参加了两种不同的活动，且分别安排在上、下午，那么不同安排方案的种数是.

查看试题解析
13. 设数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且 $\forall n \in N^{*}, a_{n + 1} > a_{n}, S_{n} \geq S_{6}$ . 请写出一个满足条件的数列 ${a_{n}}$ 的通项公式 $a_{n} =$ ．

查看试题解析
14. 已知平面内两个定点 $M (3, 0)$ 和点 $N (- 3, 0)$ ， $P$ 是动点，且直线 $P M$ , $P N$ 的斜率乘积为常数 $a (a \neq 0)$ ，设点 $P$ 的轨迹为 $C$ .
① 存在常数 $a (a \neq 0)$ ，使 $C$ 上所有点到两点 $(- 4, 0), (4, 0)$ 距离之和为定值；

② 存在常数 $a (a \neq 0)$ ，使 $C$ 上所有点到两点 $(0, - 4), (0, 4)$ 距离之和为定值；

③ 不存在常数 $a (a \neq 0)$ ，使 $C$ 上所有点到两点 $(- 4, 0), (4, 0)$ 距离差的绝对值为定值；

④ 不存在常数 $a (a \neq 0)$ ，使 $C$ 上所有点到两点 $(0, - 4), (0, 4)$ 距离差的绝对值为定值.

其中正确的命题是.（填出所有正确命题的序号）

查看试题解析

三、解答题

15. 已知函数 $f (x ） = \cos x (\sqrt{3} \sin x - \cos x) + \frac{1}{2}$ .
（I）求 $f (\frac{π}{3})$ 的值；

（II）当 $x \in [0, \frac{π}{2}]$ 时，不等式 $c < f (x) < c + 2$ 恒成立，求实数 $c$ 的取值范围．

查看试题解析
16. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为矩形，平面 $P C D$ $⊥$ 平面 $A B C D$ ， $A B = 2$ ， $B C = 1$ ， $P C = P D = \sqrt{2}$ ， $E$ 为 $P B$ 中点．

（Ⅰ）求证： $P D$ ∥平面 $A C E$ ；

（Ⅱ）求二面角 $E - A C - D$ 的余弦值；

（Ⅲ）在棱 $P D$ 上是否存在点 $M$ ，使得 $A M ⊥$ $B D$ ？若存在，求 $\frac{P M}{P D}$ 的值；若不存在，说明理由．

查看试题解析

17. 某学校为了解高一新生的体质健康状况，对学生的体质进行了测试. 现从男、女生中各随机抽取

20

人，把他们的测试数据，按照《国家学生体质健康标准》整理如下表. 规定：数据≥

60

，体质健康为合格.

等级	数据范围	男生人数	男生平均分	女生人数	女生平均分
优秀	$[90, 100]$	$5$	$91.3$	$2$	$91$
良好	$[80, 89]$	$4$	$83.9$	$4$	$84.1$
及格	$[60, 79]$	$8$	$70$	$11$	$70.2$
不及格	$60$ 以下	$3$	$49.6$	$3$	$49.1$
总计	--	$20$	$75.0$	$20$	$71.9$

(I)从样本中随机选取一名学生，求这名学生体质健康合格的概率；

(II)从男生样本和女生样本中各随机选取一人，求恰有一人的体质健康等级是优秀的概率；

（III）表中优秀、良好、及格、不及格四个等级的男生、女生平均分都接近（二者之差的绝对值不大于 $1$ ），但男生的总平均分却明显高于女生的总平均分．研究发现，若去掉四个等级中一个等级的数据，则男生、女生的总平均分也接近，请写出去掉的这个等级．（只需写出结论）

查看试题解析

18. 已知 $f (x) = (x - 1) e^{x} - \frac{1}{2} a x^{2}$ ．
(I)若曲线 $y = f (x)$ 在点 $(1, f (1))$ 处的切线与 $x$ 轴平行，求 $a$ 的值；

(II)若 $f (x)$ 在 $x = 0$ 处取得极大值，求 $a$ 的取值范围.

查看试题解析
19. 已知抛物线 $G : y^{2} = 2 p x (p > 0)$ 过点 $M (1, - 2)$ ， $A, B$ 是抛物线 $G$ 上异于点 $M$ 的不同两点，且以线段 $A B$ 为直径的圆恒过点 $M$ .
（I）当点 $A$ 与坐标原点 $O$ 重合时，求直线 $M B$ 的方程；

（II）求证：直线 $A B$ 恒过定点，并求出这个定点的坐标.

查看试题解析
20. 对于集合 $A = {a_{1}, a_{2}, \cdot \cdot \cdot, a_{n}}$ ， $B = {b_{1}, b_{2}, \cdot \cdot \cdot, b_{m}}$ ， $n \in N^{*}, m \in N^{*}$ , $A + B = {x + y | x \in A, y \in B}$ .集合 $A$ 中的元素个数记为 $| A |$ .规定：若集合 $A$ 满足 $| A + A | = \frac{n (n + 1)}{2}$ ，则称集合 $A$ 具有性质 $T$ ．
（I）已知集合 $f (x) = {\begin{matrix} 2 e^{x - 1}, x < 2 \\ \log_{3} (x^{2} - 1), x \geq 2 \end{matrix}$ ， $B = {\frac{1}{3}, \frac{2}{3}, \frac{4}{3}, \frac{8}{3}}$ ，写出 $| A + A |$ ， $| B + B |$ 的值；

（II）已知集合 $A = {a_{1}, a_{2}, \cdot \cdot \cdot, a_{n}}$ ， ${a_{n}}$ 为等比数列， $a_{n} > 0$ ，且公比为 $\frac{2}{3}$ ，证明： $A$ 具有性质 $T$ ；

（III）已知 $A, B$ 均有性质 $T$ ，且 $n = m$ ，求 $| A + B |$ 的最小值.

查看试题解析