湖北省黄石市2016-2017学年高一下学期期末数学考试试卷（理科）

试卷更新日期：2017-09-13 类型：期末考试

进入出卷网下载

一、选择题

1. 已知△ABC中，a=1，b= $\sqrt{2}$ ，B=45°，则锐角A等于（）

A、30° B、45° C、60°或 30° D、60°

查看试题解析
2. 在△ABC 中，a²=b²+c²+bc，则A等于（）

A、60° B、120° C、30° D、150°

查看试题解析
3. 如图所示是一个几何体的三视图，其中正视图是一个正三角形，则这个几何体的表面积是（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\sqrt{3}$ + $\sqrt{7}$ D、 $\sqrt{3}$ + $\sqrt{7}$ +1

查看试题解析
4. 设变量x，y满足约束条件 ${\begin{matrix} y \geq 0 \\ x - y + 1 \geq 0 \\ x + y - 3 \leq 0 \end{matrix}$ ，则z=2x+y的最大值为（）

A、﹣2 B、4 C、6 D、8

查看试题解析
5. 若a＞0，b＞0，且a+b=4则下列不等式中恒成立的是（）

A、a²+b²≥8 B、ab≥4 C、a²+b²≤8 D、ab≤2

查看试题解析
6. 设S_n是等比数列{a_n}的前n项和，a₃= $\frac{3}{2}$ ，S₃= $\frac{9}{2}$ ，则公比q=（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、1或﹣ $\frac{1}{2}$ D、1或 $\frac{1}{2}$

查看试题解析
7. 等差数列{a_n}的前n项和为S_n ，已知 $a_{m - 1} + a_{m + 1} - 2 a_{m}^{2} = 0 ， S_{2 m - 1} = 39$ 则m=（）

A、38 B、39 C、20 D、19

查看试题解析
8. 已知等比数列{a_n}中的各项都是正数，且 $a_{1} ， \frac{1}{2} a_{3} ， 2 a_{2}$ 成等差数列，则 $\frac{a_{9} + a_{10} + a_{13}}{a_{7} + a_{8} + a_{11}}$ =（）

A、 $1 + \sqrt{2}$ B、 $1 - \sqrt{2}$ C、 $3 + 2 \sqrt{2}$ D、 $3 - 2 \sqrt{2}$

查看试题解析
9. 已知两个平面垂直，下列命题： ①一个平面内的已知直线必垂直于另一个平面内的任意一条直线．
②一个平面内的已知直线必垂直于另一个平面内的无数条直线．
③一个平面内的任一条直线必垂直于另一个平面．
④一个平面内垂直于交线的直线与另一个平面垂直．
其中正确命题的个数是（）

A、3 B、2 C、1 D、0

查看试题解析
10. 已知x＞0，y＞0，且 $\frac{2}{x} + \frac{1}{y} = 1$ ，若x+2y＞m²+2m恒成立，则实数m的取值范围（）

A、m≥4或m≤﹣2 B、m≥2或m≤﹣4 C、﹣4＜m＜2 D、﹣2＜m＜4

查看试题解析
11. 已知实数x，y满足y=x²﹣2x+2，﹣1≤x≤1，则 $\frac{y + 3}{x + 2}$ 的最小值是（）

A、 $\frac{4}{3}$ B、 $2 \sqrt{13} - 6$ C、8 D、 $\frac{5}{2}$

查看试题解析
12. 如图是正方体的平面展开图，在这个正方体中，
①BM与ED平行；
②CN与BE是异面直线；
③CN与BM成60°角；
④DM与BN垂直．
以上四个命题中，正确命题的序号是（）

A、③ B、③④ C、①③ D、①③④

查看试题解析

二、填空题

13. 对于任意的实数λ∈R，直线（2λ+1）x+（λ﹣1）y+1=0恒过定点．

查看试题解析
14. 一个正三棱柱顶点都在球面上，正三棱柱的底面是正三角形，正三角形的边长是3，正三棱柱的体积是 $\frac{9 \sqrt{3}}{2}$ ，则球的体积是．

查看试题解析
15. 下面命题正确的是．
⑴两条直线a，b没有公共点，那么a与b是异面直线．
⑵如果直线a，b和平面α满足a∥平面α，b∥平面α，那么a∥b．
⑶如果直线a，b和平面α满足a∥b，a∥平面α，那么b∥平面α．
⑷若直线a不平行于平面α，则平面α内不存在与直线a平行的直线．
⑸如果直线a∥平面α，点P∈平面α，那么过点P且平行于直线a的直线只有一条，且在平面α内．

查看试题解析
16. 已知m是给定的一个常数，若直线x﹣3y+m=0上存在两点A，B，使得点P（m，0）满足|PA|=|PB|，则线段AB的中点坐标是．

查看试题解析

三、解答题

17. 求和：S_n= $\frac{1}{2}$ + $\frac{3}{2^{2}}$ + $\frac{5}{2^{3}}$ + $\frac{7}{2^{4}}$ +…+ $\frac{2 n - 1}{2^{n}}$ ．

查看试题解析
18. 已知△ABC的三个顶点是A（4，0），B（6，7），C（0，3）．

(1)、求过点A与BC平行的直线方程．

(2)、求过点B，并且在两个坐标轴上截距相等的直线方程．

查看试题解析
19. 正四棱锥V﹣ABCD中，底面ABCD是边长2为的正方形，其他四个侧面都是侧棱长为 $\sqrt{5}$ 的等腰三角形．

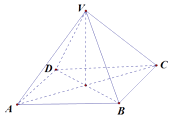(1)、求正四棱锥V﹣ABCD的体积．

(2)、求二面角V﹣BC﹣A的平面角的大小．

查看试题解析
20. 已知△ABC的三个内角A，B，C的对边分别是a，b，c，且bcosC=（2a﹣c）cosB．

(1)、求角B．

(2)、若 $b = \sqrt{13}$ ，△ABC的周长为 $\sqrt{13} + 7$ ，求△ABC的面积．

查看试题解析
21. 如图所示，四棱锥P﹣ABCD中平面PAB⊥平面ABCD，底面ABCD是正方形．点M是棱PC的中点

(1)、记平面ADM与平面PBC的交线是l，试判断直线l与BC的位置关系，并加以证明．

(2)、若 $P A = A B = 1 ， P B = \sqrt{2}$ ，求证PB⊥平面ADM，并求直线PC与平面ADM所成角的正弦值．

查看试题解析
22. 已知一个递增的等差数列{a_n}的前三项的和为﹣3，前三项的积为8．数列 ${\frac{b_{n}}{a_{n}}}$ 的前n项和为 $S_{n} = 2^{n + 1} - 2$ ．

(1)、求数列{a_n}的通项公式．

(2)、求数列 ${\frac{b_{n}}{a_{n}}}$ 的通项公式．

(3)、是否存在一个等差数列{c_n}，使得等式 $b_{n} = c_{n + 1} \cdot 2^{n + 1} - c_{n} \cdot 2^{n}$ 对所有的正整数n都成立．若存在，求出所有满足条件的等差数列{c_n}的通项公式，并求数列{b_n}的前n项和T_n；若不存在，请说明理由．

查看试题解析