黑龙江省大庆市2016-2017学年高考理数三模考试试卷

试卷更新日期：2017-09-13 类型：高考模拟

进入出卷网下载

一、选择题：

1. 已知集合A={y|0≤y＜2，y∈N}，B={x|x²﹣4x﹣5≤0，x∈N}，则A∩B=（）

A、{1} B、{0，1} C、[0，2） D、∅

查看试题解析
2. 已知复数z= $\frac{3 - 4 i}{1 - 2 i}$ ，则复数z在复平面内对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 设S_n为等差数列{a_n}的前n项和，若a₂₀₁₇=S₂₀₁₇=2017，则首项a₁=（）

A、﹣2014 B、﹣2015 C、﹣2016 D、﹣2017

查看试题解析
4. 在区间[0，1]内随机取两个数分别为a，b，则使得方程x²+2ax+b²=0有实根的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
5. 我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题：“今有垣厚十尺，两鼠对穿，初日各一尺，大鼠日自倍，小鼠日自半，问几何日相逢？”现用程序框图描述，如图所示，则输出结果n=（）

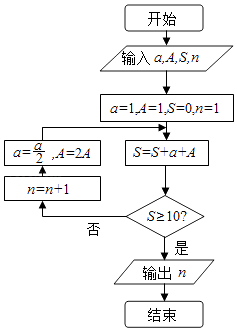A、4 B、5 C、2 D、3

查看试题解析
6. 给出下列四个命题：
①若x∈A∩B，则x∈A或x∈B；
②∀x∈（2+∞），都有x²＞2^x；
③若a，b是实数，则a＞b是a²＞b²的充分不必要条件；
④“∃x₀∈R，x₀²+2＞3x₀”的否定是“∀x∈R，x²+2≤3x”；
其中真命题的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
7. 等比数列{a_n}的公比q＞0，已知a₂=1，a_n+2+a_n+1=6a_n则{a_n}的前4项和S₄=（）

A、﹣20 B、15 C、 $\frac{15}{2}$ D、 $\frac{20}{3}$

查看试题解析
8. 函数f（x）=sin（ωx+φ）（其中|φ|＜ $\frac{π}{2}$ ）的图象如图所示，为了得到y=sinωx的图象，只需把y=f（x）的图象上所有点（）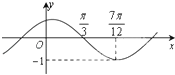

A、向左平移 $\frac{π}{12}$ 个单位长度 B、向右平移 $\frac{π}{12}$ 个单位长度 C、向左平移 $\frac{π}{6}$ 个单位长度 D、向右平移 $\frac{π}{6}$ 个单位长度

查看试题解析
9. 在平行四边形ABCD中， $| \vec{A D} | = 3 ， | \vec{A B} | = 5 ， \vec{A E} = \frac{2}{3} \vec{A D} ， \vec{B F} = \frac{1}{3} \vec{B C} ， c o s A = \frac{3}{5}$ ，则 $| \vec{E F}$ |=（）

A、 $\sqrt{14}$ B、 $2 \sqrt{5}$ C、 $4 \sqrt{2}$ D、 $2 \sqrt{11}$

查看试题解析
10. 已知某几何体的三视图如图所示，则该几何体的表面积为（）

A、 $\frac{27}{2}$ B、27 C、 $27 \sqrt{2}$ D、 $27 \sqrt{3}$

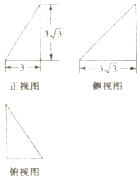查看试题解析
11. 已知点F₂ ， P分别为双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的右焦点与右支上的一点，O为坐标原点，若2 $\vec{O M} = \vec{O P} + \vec{O F_{2}} ， | \vec{O F_{2}} | = | \vec{F_{2} M}$ |，且 $\vec{O F_{2}} \cdot \vec{F_{2} M} = \frac{c^{2}}{2}$ ，则该双曲线的离心率为（）

A、 $2 \sqrt{3}$ B、 $\frac{3}{2}$ C、 $\sqrt{3}$ D、 $\frac{\sqrt{3} + 1}{2}$

查看试题解析
12. 设函数f（x）=x³﹣2ex²+mx﹣lnx，记g（x）= $\frac{f (x)}{x}$ ，若函数g（x）至少存在一个零点，则实数m的取值范围是（）

A、（﹣∞，e²+ $\frac{1}{e}$ ] B、（0，e²+ $\frac{1}{e}$ ] C、（e²+ $\frac{1}{e}$ ，+∞] D、（﹣e²﹣ $\frac{1}{e}$ ，e²+ $\frac{1}{e}$ ]

查看试题解析

二、填空题

13. 已知 $a = \int_{0}^{π} 2 s i n \frac{x}{2} c o s \frac{x}{2} d x$ ，则a= ．

查看试题解析
14. 不等式组 ${\begin{matrix} x \geq 0 \\ x + y \leq 3 \\ y \geq x + 1 \end{matrix}$ 表示的平面区域为Ω，直线y=kx﹣1与区域Ω有公共点，则实数k的取值范围为．

查看试题解析
15. 某校高三年级要从5名男生和2名女生中任选3名代表参加数学竞赛（每人被选中的机会均等），则在男生甲被选中的情况下，男生乙和女生丙至少一个被选中的概率是．

查看试题解析
16. 已知函数f（x）是定义在R上的奇函数，且当x∈（0，+∞）时，都有不等式f（x）+xf'（x）＞0成立，若 $a = 4^{0.2} f (4^{0.2}) ， b = (l o g_{4} 3) f (l o g_{4} 3) ， c = (l o g_{4} \frac{1}{16}) f (l o g_{4} \frac{1}{16})$ ，则a，b，c的大小关系是．

查看试题解析

三、解答题

17. 已知在△ABC中，角A，B，C的对边分别为a，b，c，且 $\frac{c o s B}{b}$ + $\frac{c o s C}{c}$ = $\frac{2 \sqrt{3} s i n A}{3 s i n C}$ ．

(1)、求b的值；

(2)、若cosB+ $\sqrt{3}$ sinB=2，求a+c的取值范围．

查看试题解析
18. 五一期间，某商场决定从2种服装、3种家电、4种日用品中，选出3种商品进行促销活动．

(1)、试求选出3种商品中至少有一种是家电的概率；

(2)、商场对选出的某商品采用抽奖方式进行促销，即在该商品现价的基础上将价格提高60元，规定购买该商品的顾客有3次抽奖的机会：若中一次奖，则获得数额为n元的奖金；若中两次奖，则获得数额为3n元的奖金；若中三次奖，则共获得数额为 6n元的奖金．假设顾客每次抽奖中奖的概率都是 $\frac{1}{4}$ ，请问：商场将奖金数额n最高定为多少元，才能使促销方案对商场有利？

查看试题解析
19. 如图，在四棱锥P﹣ABCD．中，PC⊥底面ABCD，ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2AD=2CD=2．E是PB的中点．
（Ⅰ）求证；平面EAC⊥平面PBC；
（Ⅱ）若二面角P﹣AC﹣E的余弦值为 $\frac{\sqrt{3}}{3}$ ，求直线PA与平面EAC所成角的正弦值．

查看试题解析
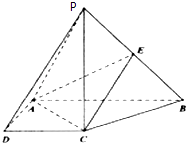20. 已知中心在原点O，焦点在x轴上的椭圆，离心率 $e = \frac{1}{2}$ ，且椭圆过点 $(1 ， \frac{3}{2})$ ．
（Ⅰ）求椭圆的方程；
（Ⅱ）椭圆左，右焦点分别为F₁ ， F₂ ，过F₂的直线l与椭圆交于不同的两点A、B，则△F₁AB的内切圆的面积是否存在最大值？若存在，求出这个最大值及此时的直线方程；若不存在，请说明理由．

查看试题解析
21. 已知函数 f（x）=2lnx+x²﹣ax．
（Ⅰ）当a=5时，求f（x）的单调区间；
（Ⅱ）设A（x₁ ， y₁），B（x₂ ， y₂）是曲线y=f（x）图象上的两个相异的点，若直线AB的斜率k＞1恒成立，求实数a的取值范围；
（Ⅲ）设函数f（x）有两个极值点x₁ ， x₂ ， x₁＜x₂且x₂＞e，若f（x₁）﹣f（x₂）≥m恒成立，求实数m的取值范围．

查看试题解析
22. 将圆 ${\begin{matrix} x = 2 c o s θ \\ y = 2 s i n θ \end{matrix} (θ$ 为参数）上的每一点的横坐标保持不变，纵坐标变为原来的 $\frac{1}{2}$ 倍，得到曲线C．

(1)、求出C的普通方程；

(2)、设直线l：x+2y﹣2=0与C的交点为P₁ ， P₂ ，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，
求过线段P₁P₂的中点且与l垂直的直线的极坐标方程．

查看试题解析
23. 已知函数f（x）=|x|+|x﹣3|．

(1)、解关于x的不等式f（x）﹣5≥x；

(2)、设m，n∈{y|y=f（x）}，试比较mn+4与2（m+n）的大小．

查看试题解析