湖北省黄冈市2016-2017学年高一下学期期末数学考试试卷(理科)
试卷更新日期:2017-09-13 类型:期末考试
一、选择题
-
1. 下列结论正确的是( )A、若a>b,则ac2>bc2 B、若a2>b2 , 则a>b C、若a>b,c<0,则a+c<b+c D、若 < ,则a<b2. 设数列{an}是等差数列,若a2+a4+a6=12,则a1+a2+…+a7等于( )A、14 B、21 C、28 D、353. 设l,m是两条不同的直线,α是一个平面,则下列命题正确的是( )A、若l⊥m,m⊂α,则l⊥α B、若l⊥α,l∥m,则m⊥α C、若l∥α,m⊂α,则l∥m D、若l∥α,m∥α,则l∥m4. 在△ABC中,内角A,B,C所对的边分别是a,b,c,若3a=2b,则 的值为( )A、﹣ B、 C、1 D、5. 已知等比数列{an}中,a3=2,a4a6=16,则 =( )A、2 B、4 C、8 D、166. 从点(2,3)射出的光线沿斜率k= 的方向射到y轴上,则反射光线所在的直线方程为( )A、x+2y﹣4=0 B、2x+y﹣1=0 C、x+6y﹣16=0 D、6x+y﹣8=07. 若α,β为锐角,且满足cosα= ,cos(α+β)= ,则sinβ的值为( )A、﹣ B、 C、 D、8. 若动点A(x1 , y2)、B(x2 , y2)分别在直线l1:x+y﹣11=0和l2:x+y﹣1=0上移动,则AB中点M所在直线方程为( )A、x﹣y﹣6=0 B、x+y+6=0 C、x﹣y+6=0 D、x+y﹣6=09. 已知某几何体的三视图如图所示,其中,正(主)视图,侧(左)视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为( )
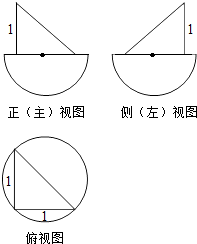 A、 B、 C、 D、10. 将正偶数集合{2,4,6,…}从小到大按第n组有2n个偶数进行分组:{2,4},{6,8,10,12},{14,16,18,20,22,24},…,则2018位于( )组.A、30 B、31 C、32 D、3311. 已知实数x,y满足 ,则ω= 的取值范围是( )A、[﹣1, ] B、[﹣ , ] C、[﹣ ,1) D、[﹣ ,+∞)12. 在正方体ABCD﹣A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值t构成的集合是( )
A、 B、 C、 D、10. 将正偶数集合{2,4,6,…}从小到大按第n组有2n个偶数进行分组:{2,4},{6,8,10,12},{14,16,18,20,22,24},…,则2018位于( )组.A、30 B、31 C、32 D、3311. 已知实数x,y满足 ,则ω= 的取值范围是( )A、[﹣1, ] B、[﹣ , ] C、[﹣ ,1) D、[﹣ ,+∞)12. 在正方体ABCD﹣A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值t构成的集合是( )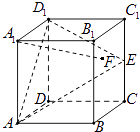 A、{t| } B、{t| ≤t≤2} C、{t|2 } D、{t|2 }
A、{t| } B、{t| ≤t≤2} C、{t|2 } D、{t|2 }二、填空题
-
13. 若关于x的不等式ax2﹣6x+a2<0的解集是(1,m),则m= .14. 若 ,则tan2α= .15. 若△ABC的面积为 ,BC=2,C=60°,则边AB的长度等于 .16. 已知不等式组 表示的平面区域为D,则(1)、z=x2+y2的最小值为 .(2)、若函数y=|2x﹣1|+m的图象上存在区域D上的点,则实数m的取值范围是 .
三、解答题
-
17. 在平面直角坐标系内,已知A(1,a),B(﹣5,﹣3),C(4,0);(1)、当a∈( ,3)时,求直线AC的倾斜角α的取值范围;(2)、当a=2时,求△ABC的BC边上的高AH所在直线方程l.18. 在△ABC中,a,b,c分别是角A,B,C的对边, = ,且a+c=2.(1)、求角B;(2)、求边长b的最小值.19. 已知A(4,﹣3),B(2,﹣1)和直线l:4x+3y﹣2=0.(1)、求在直角坐标平面内满足|PA|=|PB|的点P的方程;(2)、求在直角坐标平面内一点P满足|PA|=|PB|且点P到直线l的距离为2的坐标.20. 如图所示的多面体,它的正视图为直角三角形,侧视图为正三角形,俯视图为正方形(尺寸如图所示),E为VB的中点.
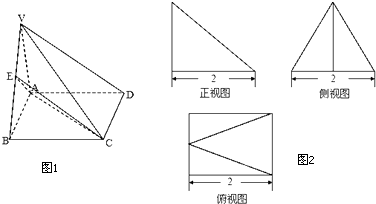 (1)、求证:VD∥平面EAC;(2)、求二面角A﹣VB﹣D的余弦值.21. 某投资公司计划投资A,B两种金融产品,根据市场调查与预测,A产品的利润y1与投资金额x的函数关系为y1=18﹣ ,B产品的利润y2与投资金额x的函数关系为y2= (注:利润与投资金额单位:万元).(1)、该公司已有100万元资金,并全部投入A,B两种产品中,其中x万元资金投入A产品,试把A,B两种产品利润总和表示为x的函数,并写出定义域;(2)、在(1)的条件下,试问:怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?22. 已知曲线f(x)= (x>0)上有一点列Pn(xn , yn)(n∈N*),过点Pn在x轴上的射影是Qn(xn , 0),且x1+x2+x3+…+xn=2n+1﹣n﹣2.(n∈N*)(1)、求数列{xn}的通项公式;(2)、设四边形PnQnQn+1Pn+1的面积是Sn , 求Sn;(3)、在(2)条件下,求证: + +…+ <4.
(1)、求证:VD∥平面EAC;(2)、求二面角A﹣VB﹣D的余弦值.21. 某投资公司计划投资A,B两种金融产品,根据市场调查与预测,A产品的利润y1与投资金额x的函数关系为y1=18﹣ ,B产品的利润y2与投资金额x的函数关系为y2= (注:利润与投资金额单位:万元).(1)、该公司已有100万元资金,并全部投入A,B两种产品中,其中x万元资金投入A产品,试把A,B两种产品利润总和表示为x的函数,并写出定义域;(2)、在(1)的条件下,试问:怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?22. 已知曲线f(x)= (x>0)上有一点列Pn(xn , yn)(n∈N*),过点Pn在x轴上的射影是Qn(xn , 0),且x1+x2+x3+…+xn=2n+1﹣n﹣2.(n∈N*)(1)、求数列{xn}的通项公式;(2)、设四边形PnQnQn+1Pn+1的面积是Sn , 求Sn;(3)、在(2)条件下,求证: + +…+ <4.