河南省郑州市2016-2017学年高一下学期期末数学考试试卷
试卷更新日期:2017-09-13 类型:期末考试
一、选择题
-
1. sin660°的值为( )A、 B、 C、 D、﹣2. 把黑、红、白3张纸牌分给甲、乙、丙三人,每人一张,则事件“甲分得黑牌”与“乙分得黑牌”是( )A、对立事件 B、必然事件 C、不可能事件 D、互斥但不对立事件3. 某产品的广告费用x万元与销售额y万元的统计数据如下表
广告费用x(万元)
2
3
4
5
销售额y(万元)
26
m
49
54
根据上表可得回归方程 =9x+10.5,则m为( )
A、36 B、37 C、38 D、394. 已知数据x1 , x2 , x3 , …,xn是上海普通职工n(n≥3,n∈N*)个人的年收入,设这n个数据的中位数为x,平均数为y,方差为z,如果再加上世界首富的年收入xn+1 , 则这n+1个数据中,下列说法正确的是( )A、年收入平均数大大增大,中位数一定变大,方差可能不变 B、年收入平均数大大增大,中位数可能不变,方差变大 C、年收入平均数大大增大,中位数可能不变,方差也不变 D、年收入平均数可能不变,中位数可能不变,方差可能不变5. 下列函数中,周期为π,且在( , )上单调递减的是( )A、y=sinxcosx B、y=sinx+cosx C、y=tan(x+ ) D、y=2cos22x﹣16. 的值为( )A、 B、 C、 D、7. 某程序框图如图所示,若输出的S=120,则判断框内为( )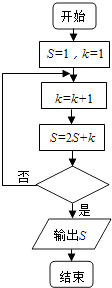 A、k>4? B、k>5? C、k>6? D、k>7?8. 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< )的部分图象如图所示,下列说法正确的是( )
A、k>4? B、k>5? C、k>6? D、k>7?8. 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< )的部分图象如图所示,下列说法正确的是( )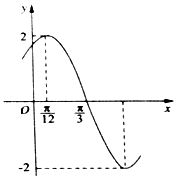 A、函数f(x)的图象关于直线x=﹣ 对称 B、函数f(x)的图象关于点(﹣ ,0)对称 C、若方程f(x)=m在[﹣ ,0]上有两个不相等的实数根,则实数m∈(﹣2,﹣ ] D、将函数f(x)的图象向左平移 个单位可得到一个偶函数9. 要得到函数 的图象,只需将函数y=cos2x的图象( )A、向左平移 个单位 B、向右平移 个单位 C、向左平移 个单位 D、向右平移 个单位10. 已知在矩形ABCD中,AB= ,BC=3,点E满足 = ,点F在边CD上,若 • =1,则 • =( )A、1 B、2 C、 D、311. 已知sin( ﹣α)= ,则cos(2α+ )=( )A、﹣ B、 C、 D、﹣12. 如图,设Ox、Oy是平面内相交成45°角的两条数轴, 、 分别是x轴、y轴正方向同向的单位向量,若向量 =x +y ,则把有序数对(x,y)叫做向量 在坐标系xOy中的坐标,在此坐标系下,假设 =(﹣2,2 ), =(2,0), =(5,﹣3 ),则下列命题不正确的是( )
A、函数f(x)的图象关于直线x=﹣ 对称 B、函数f(x)的图象关于点(﹣ ,0)对称 C、若方程f(x)=m在[﹣ ,0]上有两个不相等的实数根,则实数m∈(﹣2,﹣ ] D、将函数f(x)的图象向左平移 个单位可得到一个偶函数9. 要得到函数 的图象,只需将函数y=cos2x的图象( )A、向左平移 个单位 B、向右平移 个单位 C、向左平移 个单位 D、向右平移 个单位10. 已知在矩形ABCD中,AB= ,BC=3,点E满足 = ,点F在边CD上,若 • =1,则 • =( )A、1 B、2 C、 D、311. 已知sin( ﹣α)= ,则cos(2α+ )=( )A、﹣ B、 C、 D、﹣12. 如图,设Ox、Oy是平面内相交成45°角的两条数轴, 、 分别是x轴、y轴正方向同向的单位向量,若向量 =x +y ,则把有序数对(x,y)叫做向量 在坐标系xOy中的坐标,在此坐标系下,假设 =(﹣2,2 ), =(2,0), =(5,﹣3 ),则下列命题不正确的是( )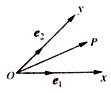 A、 =(1,0) B、| |=2 C、 ∥ D、 ⊥
A、 =(1,0) B、| |=2 C、 ∥ D、 ⊥二、填空题
-
13. 已知向量 =(2,3), =(﹣4,1),则向量 在向量 方向上的投影为 .14. 在△ABC中,cosA=﹣ ,sinB= ,则cosC= .15. 若 =2,则tan(α﹣ )= .16. 已知 =(2,0), =(1, ),若(1﹣λ) +λ ﹣ = (λ∈R),则| |的最小值为 .
三、解答题
-
17. 已知向量 =(1,2), =(﹣3,4).(1)、求 + 与 ﹣ 的夹角;(2)、若 满足 ⊥( + ),( + )∥ ,求 的坐标.18. 中国国家主席习近平在2013年提出共建丝绸之路经济带和21世纪海上丝绸之路的重要合作倡议,3年来,“一带一路”建设进展顺利,成果丰硕,受到国际社会的广泛欢迎和高度评价,某地区在“一带一路”项目开展之前属于欠发达区域,为了解“一带一路”项目开展以后对居民的收入情况的影响.前期对居民的月收入情况调查了10000人,并所得数据画了样本频率分布直方图,每个分组包含左端点,不包含右端点.
 (1)、求居民朋收入在[3000,4000)的频率;(2)、根据频率分布直方图求样本数据的中位数、平均数.19. 已知函数f(x)= cos(2x﹣ ).(1)、若sinθ=﹣ ,θ∈( ,2π),求f(θ+ )的值;(2)、若x∈[ , ],求函数f(x)的单调减区间.20. 为了促进学生的全面发展,郑州市某中学重视学生社团文化建设,现用分层抽样的方法从“话剧社”,“创客社”,“演讲社”三个金牌社团中抽取6人组成社团管理小组,有关数据见表(单位:人):
(1)、求居民朋收入在[3000,4000)的频率;(2)、根据频率分布直方图求样本数据的中位数、平均数.19. 已知函数f(x)= cos(2x﹣ ).(1)、若sinθ=﹣ ,θ∈( ,2π),求f(θ+ )的值;(2)、若x∈[ , ],求函数f(x)的单调减区间.20. 为了促进学生的全面发展,郑州市某中学重视学生社团文化建设,现用分层抽样的方法从“话剧社”,“创客社”,“演讲社”三个金牌社团中抽取6人组成社团管理小组,有关数据见表(单位:人):社团名称
成员人数
抽取人数
话剧社
50
a
创客社
150
b
演讲社
100
c
(1)、求a,b,c的值;(2)、若从“话剧社”,“创客社”,“演讲社”已抽取的6人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.21. 已知对任意平面向量 =(x,y),把 绕其起点沿逆时针方向旋转θ角得到的向量 =(xcosθ﹣ysinθ,xsinθ+ycosθ),叫做把点B绕点A逆时针方向旋转θ得到点P.(1)、已知平面内点A(2,3),点B(2+2 ,1).把点B绕点A逆时针方向旋转 角得到点P,求点P的坐标.(2)、设平面内曲线C上的每一点绕坐标原点沿顺时针方向旋转 后得到的点的轨迹方程是曲线y= ,求原来曲线C的方程.22. 已知函数f(x)= cos4x+2sinxcosx﹣ sin4x.(1)、当x∈[0, ]时,求f(x)的最大值、最小值以及取得最值时的x值;(2)、设g(x)=3﹣2m+mcos(2x﹣ )(m>0),若对于任意x1∈[0, ],都存在x2∈[0, ],使得f(x1)=g(x2)成立,求实数m的取值范围.