福建省漳州市2016-2017学年高考文数二模考试试卷
试卷更新日期:2017-09-13 类型:高考模拟
一、选择题:
-
1. 已知A={x|x+1>0},B={﹣2,﹣1,0,1},则(∁RA)∩B=( )A、{﹣2,﹣1} B、{﹣2} C、{﹣2,0,1} D、{0,1}2. 复数 的虚部为( )A、 B、 C、 D、3. 在数列{an}中,a1=2,an+1=an+2,Sn为{an}的前n项和,则S10=( )A、90 B、100 C、110 D、1304. 五张卡片上分别写有数字1、2、3、4、5,从这五张卡片中随机抽取2张,则取出的2张卡片上数字之和为奇数的概率为( )A、 B、 C、 D、5. 为了得到函数y=cos2x的图象,只要把函数 的图象上所有的点( )A、向右平行移动 个单位长度 B、向左平行移动 个单位长度 C、向右平行移动 个单位长度 D、向左平行移动 个单位长度6. 如图,网格纸的小正方形的边长是1,粗线表示一正方体被某平面截得的几何体的三视图,则该几何体的体积为( )
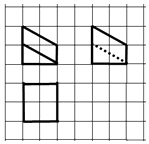 A、2 B、4 C、6 D、87. 已知函数 ,若 ,则f(1﹣m)=( )A、﹣1 B、﹣4 C、﹣9 D、﹣168. 如图为中国传统智力玩具鲁班锁,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,六根完全相同的正四棱柱分成三组,经90°榫卯起来.现有一鲁班锁的正四棱柱的底面正方形边长为1,欲将其放入球形容器内(容器壁的厚度忽略不计),若球形容器表面积的最小值为30π,则正四棱柱体的高为( )
A、2 B、4 C、6 D、87. 已知函数 ,若 ,则f(1﹣m)=( )A、﹣1 B、﹣4 C、﹣9 D、﹣168. 如图为中国传统智力玩具鲁班锁,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,六根完全相同的正四棱柱分成三组,经90°榫卯起来.现有一鲁班锁的正四棱柱的底面正方形边长为1,欲将其放入球形容器内(容器壁的厚度忽略不计),若球形容器表面积的最小值为30π,则正四棱柱体的高为( )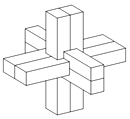 A、 B、 C、 D、59. 函数f(x)=(1+cosx)sinx在[﹣π,π]的图象的大致形状是( )A、
A、 B、 C、 D、59. 函数f(x)=(1+cosx)sinx在[﹣π,π]的图象的大致形状是( )A、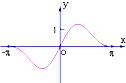 B、
B、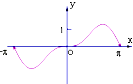 C、
C、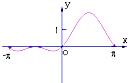 D、
D、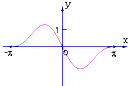 10. 一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )
10. 一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )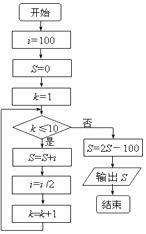 A、小球第10次着地时向下的运动共经过的路程 B、小球第11次着地时向下的运动共经过的路程 C、小球第10次着地时一共经过的路程 D、小球第11次着地时一共经过的路程11. 若P为可行域 内的一点,过P的直线l与圆O:x2+y2=7交于A,B两点,则|AB|的最小值为( )A、 B、 C、 D、12. 若不等式ln(x+2)+a(x2+x)≥0对于任意的x∈[﹣1,+∞)恒成立,则实数a的取值范围是( )A、[0,+∞) B、[0,1] C、[0,e] D、[﹣1,0]
A、小球第10次着地时向下的运动共经过的路程 B、小球第11次着地时向下的运动共经过的路程 C、小球第10次着地时一共经过的路程 D、小球第11次着地时一共经过的路程11. 若P为可行域 内的一点,过P的直线l与圆O:x2+y2=7交于A,B两点,则|AB|的最小值为( )A、 B、 C、 D、12. 若不等式ln(x+2)+a(x2+x)≥0对于任意的x∈[﹣1,+∞)恒成立,则实数a的取值范围是( )A、[0,+∞) B、[0,1] C、[0,e] D、[﹣1,0]二、填空题:
-
13. 设向量 ,且 ∥ ,则x= .14. 已知双曲线 的离心率等于2,其两条渐近线与抛物线y2=2px(p>0)的准线分别交于A,B两点,O为坐标原点, ,则p= .15. 甲、乙、丙三位同学获得某项竞赛活动的前三名,但具体名次未知.3人作出如下预测:
甲说:我不是第三名;
乙说:我是第三名;
丙说:我不是第一名.
若甲、乙、丙3人的预测结果有且只有一个正确,由此判断获得第一名的是 .
16. 设{an}是由正数组成的等比数列,Sn是{an}的前n项和.已知a2a4=16,S3=28,则a1a2…an最大时,n的值为 .三、解答题:
-
17. △ABC的内角A,B,C的对边分别为a,b,c,其中b≠c,且bcosB=ccosC,延长线段BC到点D,使得BC=4CD=4,∠CAD=30°,

(Ⅰ)求证:∠BAC是直角;
(Ⅱ)求tan∠D的值.
18. 如图1,四边形ABCD是菱形,且∠A=60°,AB=2,E为AB的中点,将四边形EBCD沿DE折起至EDC1B1 , 如图2.
(Ⅰ) 求证:平面ADE⊥平面AEB1;
(Ⅱ) 若二面角A﹣DE﹣C1的大小为 ,求三棱锥C1﹣AB1D的体积.
19. 漳州水仙鳞茎硕大,箭多花繁,色美香郁,素雅娟丽,有“天下水仙数漳州”之美誉.现某水仙花雕刻师受雇每天雕刻250粒水仙花,雕刻师每雕刻一粒可赚1.2元,如果雕刻师当天超额完成任务,则超出的部分每粒赚1.7元;如果当天未能按量完成任务,则按实际完成的雕刻量领取当天工资.(I)求雕刻师当天收入(单位:元)关于雕刻量n(单位:粒,n∈N)的函数解析式f(n);
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量n(单位:粒),整理得如表:
雕刻量n
210
230
250
270
300
频数
1
2
3
3
1
以10天记录的各雕刻量的频率作为各雕刻量发生的概率.
(ⅰ)求该雕刻师这10天的平均收入;
(ⅱ)求该雕刻师当天收入不低于300元的概率.
20. 已知椭圆 的左,右焦点分别为F1 , F2 , 过F1任作一条与两坐标轴都不垂直的直线,与C交于A,B两点,且△ABF2的周长为8.当直线AB的斜率为 时,AF2与x轴垂直.(I)求椭圆C的方程;
(Ⅱ)在x轴上是否存在定点M,总能使MF1平分∠AMB?说明理由.