河南省濮阳市2016-2017学年高一下学期期末数学考试试卷（理科）

试卷更新日期：2017-09-13 类型：期末考试

进入出卷网下载

一、选择题

1. 某中学有高中生3500人，初中生1500人，为了解学生的学习情况，用分层抽样的方法从该校学生中抽取一个容量为n的样本，已知从高中生中抽取70人，则n为（）

A、100 B、150 C、200 D、250

查看试题解析
2. 已知变量x与y正相关，且由观测数据算得样本平均数 $\bar{x}$ =3， $\bar{y}$ =3.5，则由该观测数据算得的线性回归方程可能是（）

A、 $\hat{y}$ =0.4x+2.3 B、 $\hat{y}$ =2x﹣2.4 C、 $\hat{y}$ =﹣2x+9.5 D、 $\hat{y}$ =﹣0.3x+4.4

查看试题解析
3. 设集合A={x|y=log₂（3﹣x）}，B={y|y=2^x ， x∈[0，2]}则A∩B=（）

A、[0，2] B、（1，3） C、[1，3） D、（1，4）

查看试题解析
4. 已知点P（sin $\frac{3}{4}$ π，cos $\frac{3}{4}$ π）落在角θ的终边上，且θ∈[0，2π），则θ的值为（）

A、 $\frac{π}{4}$ B、 $\frac{3 π}{4}$ C、 $\frac{5 π}{4}$ D、 $\frac{7 π}{4}$

查看试题解析
5. 函数f（x）=2^x+3x的零点所在的一个区间（）

A、（﹣2，﹣1） B、（﹣1，0） C、（0，1） D、（1，2）

查看试题解析
6. 如图是求样本x₁ ， x₂ ， …，x₁₀平均数 $\bar{x}$ 的程序框图，图中空白框中应填入的内容为（）

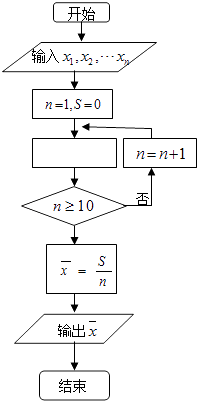A、S=S+x_n B、S=S+ $\frac{x_{n}}{n}$ C、S=S+n D、S=S+ $\frac{1}{n}$

查看试题解析
7. 已知直线l，m，平面α，β，且l⊥α，m⊂β，给出下列四个命题：
①若α∥β，则l⊥m；
②若l⊥m，则α∥β；
③若α⊥β，则l∥m；
④若l∥m，则α⊥β
其中正确命题的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
8. 光线沿直线y=2x+1射到直线y=x上，被直线y=x反射后的光线所在的直线方程为（）

A、 $y = \frac{1}{2} x - 1$ B、 $y = \frac{1}{2} x - \frac{1}{2}$ C、 $y = \frac{1}{2} x + \frac{1}{2}$ D、 $y = \frac{1}{2} x + 1$

查看试题解析
9. 某几何体的三视图如图所示，且该几何体的体积是3，则正视图中的x的值是（）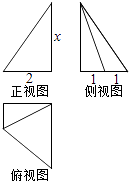

A、2 B、 $\frac{9}{2}$ C、 $\frac{3}{2}$ D、3

查看试题解析
10. 已知P是边长为2的正三角形ABC边BC上的动点，则 $\vec{A P} \cdot (\vec{A B} + \vec{A C})$ 的值（）

A、是定值6 B、最大值为8 C、最小值为2 D、与P点位置有关

查看试题解析
11. 已知函数f（x）=sinπx的图象的一部分如左图，则右图的函数图象所对应的函数解析式为（）

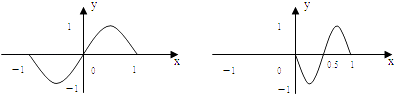A、 $y = f (2 x - \frac{1}{2})$ B、y=f（2x﹣1） C、 $y = f (\frac{x}{2} - 1)$ D、 $y = f (\frac{x}{2} - \frac{1}{2})$

查看试题解析
12. 函数y=f（x）的定义域为（﹣a，0）∪（0，a）（0＜a＜1），其图象上任意一点P（x，y）满足x²+y²=1，则给出以下四个命题：①函数y=f（x）一定是偶函数；②函数y=f（x）可能是奇函数；③函数y=f（x）在（0，a）上单调递增④若函数y=f（x）是偶函数，则其值域为（a² ， 1）其中正确的命题个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

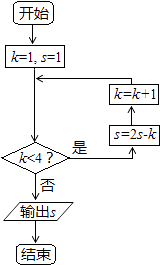
13. 阅读图所示的程序框图，运行相应地程序，输出的s值等于．

查看试题解析
14. 在如图所示的方格柢中，向量 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ 的起点和终点均在格点（小正方形顶点）上，若 $\vec{c}$ 与x $\vec{a}$ +y $\vec{b}$ （x，y为非零实数）共线，则 $\frac{x}{y}$ 的值为．

查看试题解析
15. 已知直线ax+y﹣2=0与圆心为C的圆（x﹣1）²+（y﹣a）²=4相交于A，B两点，且△ABC为等边三角形，则实数a= ．

查看试题解析
16. 已知事件在矩ABCD的边CD上随意取一点P，使得△APB的最大边是AB发生的概率为 $\frac{1}{2}$ ，则 $\frac{A D}{A B}$ = ．

查看试题解析

三、解答题

17. 已知函数f（x）= $(\frac{1}{2^{x} - 1} + \frac{1}{2}) \cdot x$ ．

(1)、求函数f（x）的定义域；

(2)、判断函数f（x）的奇偶性；

(3)、求证：f（x）＞0．

查看试题解析
18. 某实验室一天的温度（单位：℃）随时间t（单位：h）的变化近似满足函数关系：
f（t）=10﹣ $\sqrt{3} c o s \frac{π}{12} t - s i n \frac{π}{12} t$ ，t∈[0，24）
（Ⅰ）求实验室这一天的最大温差；
（Ⅱ）若要求实验室温度不高于11℃，则在哪段时间实验室需要降温？

查看试题解析

19. 某产品的三个质量指标分别为x，y，z，用综合指标S=x+y+z评价该产品的等级．若S≤4，则该产品为一等品．现从一批该产品中，随机抽取10件产品作为样本，其质量指标列表如下：

产品编号	A₁	A₂	A₃	A₄	A₅
质量指标（x，y，z）	（1，1，2）	（2，1，1）	（2，2，2）	（1，1，1）	（1，2，1）
产品编号	A₆	A₇	A₈	A₉	A₁₀
质量指标（x，y，z）	（1，2，2）	（2，1，1）	（2，2，1）	（1，1，1）	（2，1，2）

(1)、利用上表提供的样本数据估计该批产品的一等品率．

(2)、在该样品的一等品中，随机抽取2件产品，

①用产品编号列出所有可能的结果；

②设事件B为“在取出的2件产品中，每件产品的综合指标S都等于4”，求事件B发生的概率．

查看试题解析

20. 已知向量 $\vec{a}$ =（cosα，sinα）， $\vec{b}$ =（cosβ，sinβ），0＜β＜α＜π．

(1)、若| $\vec{a}$ ﹣ $\vec{b}$ |= $\sqrt{2}$ ，求证： $\vec{a}$ ⊥ $\vec{b}$ ；

(2)、设c=（0，1），若 $\vec{a}$ + $\vec{b}$ =c，求α，β的值．

查看试题解析
21. 如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，PD=DC=BC=1，AB=2，AB∥DC，∠BCD=90°．

(1)、求证：PC⊥BC；

(2)、求点A到平面PBC的距离．

查看试题解析
22. 已知圆C：x²+y²+2x+a=0上存在两点关于直线l：mx+y+1=0对称．
（I）求m的值；
（Ⅱ）直线l与圆C交于A，B两点， $\vec{O A}$ • $\vec{O B}$ =﹣3（O为坐标原点），求圆C的方程．

查看试题解析